动态规划（Dynamic Programming，DP）

核心思想

在解决一个棘手问题时，将问题分解成离散的子问题，通过先解决子问题，再逐步的解决大问题。

与分治算法的异同

• 相同点：两者的基本思想都是将待求解的问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。
• 不同点：分治算法分解得到的子问题往往都是独立的，相互之间无关，如快速排序。而动态规划分解得到的子问题往往不是相互独立的，即下一个子问题求解往往是建立在对上一个子问题的求解的基础上进一步求解。

---

经典问题1——01背包问题

假如你是个小偷，背着一个可装4磅东西的背包，你可以盗窃的商品有如下三种：
1）音响（3000美元，4磅）
2）笔记本电脑 （2000美元，3磅）
3）吉他 （1500美元，1磅）
为了让盗窃的商品价值更高，你该选择那些商品？价值为多少？

1. 简单方法

尝试各种可能的商品组合，并找出价值最高的组合。3件商品，共$2^3$种组合方法，可以看出当商品的种类增加时，这种方法非常慢，时间复杂度为$O(2^n)$。

2. 贪心算法

每次选择，都选择满足条件的单价最高的商品。我们可以用较少的开销找出近似解，在本题中，使用贪心算法最后的结果是“音响”，但是近似解不一定是最优解，实际可偷的商品价值最高的是“笔记本电脑+吉他”。

3. 动态规划

在解决4磅容量背包问题时，我们可以先解决3磅容量背包问题，2磅…，1磅…。把从3件东西中挑选价值最高的问题简化成从2件东西…，从1件东西…。通过对子问题的求解，逐步解决原来的大问题。

每个动态规划算法都是从一个网格开始，背包问题的网格如下。

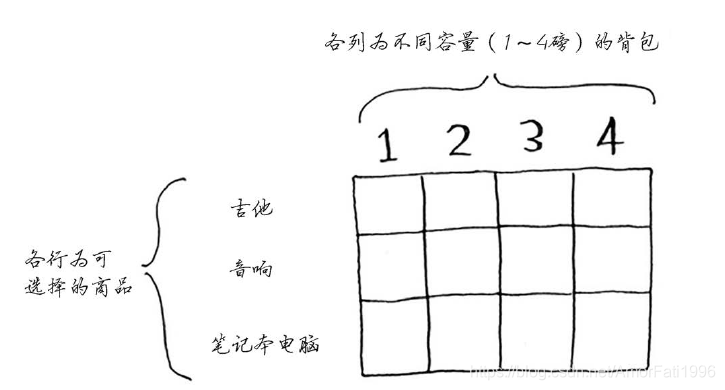
我们只需从上到下逐行（或从左至右逐列）填充该表格，当表格填满后，我们便得到了问题的答案。

• 吉他行：因为可以偷的当前只有吉他，且吉他重量为1磅，所以吉他行应该都添“吉他，1500美元”。
• 音响行：音响重量为4磅，所以前3个网格依然只能偷吉他，因为音响的价值比吉他高，所以第四个网格添“音响，3000美元”。
• 笔记本电脑行：因为笔记本电脑重量为3磅，所以前2个网格保持不变，依旧是吉他，第3个网格因为笔记本电脑的价格比吉他高，所以添笔记本电脑，第四个网格，因为笔记本电脑和吉他的加格比音响贵，所以应该添“笔记本电脑、吉他，3500美元“，也即本题答案。

最终网格应如下图所示。

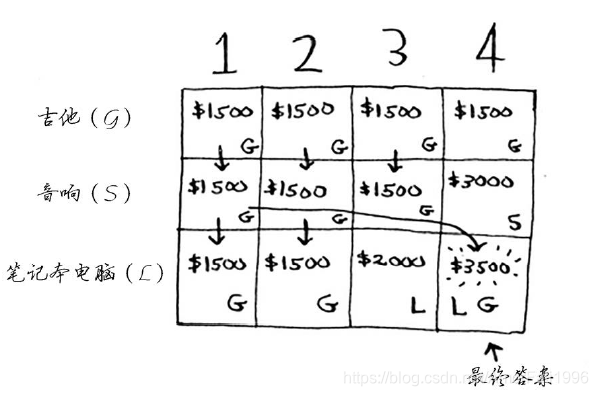
通过如上分析，我们可以通过如下公式来计算每个网格的值。

实现代码如下：

public class KnapsackProblem {
    
    

    public static void knapsackProblem(int[] weight, int[] value, int capacity) {
    
    

        //记录不同容量不同商品数量的总价值
        //为了方便理解和编写，我们从数组的第一行第一列开始统计
        int[][] totalValue = new int[weight.length + 1][capacity + 1];
        //记录对应位置应该装的商品id
        String[][] goods = new String[weight.length + 1][capacity + 1];

        //初始化：避免null, 与算法无关
        for (int i = 0; i < totalValue.length; i++) {
    
    
            goods[i][0] = "";
        }
        for (int j = 0; j < totalValue[0].length; j++) {
    
    
            goods[0][j] = "";
        }

        for (int i = 1; i < totalValue.length; i++) {
    
    
            for (int j = 1; j < totalValue[i].length; j++) {
    
    
                //判断每个网格放入的内容
                if (weight[i - 1] <= j) {
    
    
                    int temp = value[i - 1] + totalValue[i - 1][j - weight[i - 1]];
                    if (temp > totalValue[i - 1][j]) {
    
    
                        totalValue[i][j] = temp;
                        goods[i][j] = (i - 1) + " " + goods[i - 1][j - weight[i - 1]];
                    } else {
    
    
                        totalValue[i][j] = totalValue[i - 1][j];
                        goods[i][j] = goods[i - 1][j];
                    }

                } else {
    
    
                    totalValue[i][j] = totalValue[i - 1][j];
                    goods[i][j] = goods[i - 1][j];
                }
            }
        }

        System.out.println("应该偷的商品序号：" + goods[weight.length][capacity]);
        System.out.println("商品总价值：" + totalValue[weight.length][capacity]);

    }

    public static void main(String[] args) {
    
    
        int[] weight = new int[]{
    
    1, 4, 3};
        int[] value = new int[]{
    
    1500, 3000, 2000};
        int capacity = 4;
        knapsackProblem(weight, value, capacity);

    }

}

如何判断该问题是否可以用动态规划来解决？

① 需要在给定约束条件下优化某种指标时，可以采用动态规划。
② 该问题可以分解为子问题，可以对子问题的求解推进该问题的求解。

如何使用动态规划解决问题？

① 每种动态规划解决方案都涉及到网格，网格中每个单元格都代表着该问题的一个子问题，所以最关键的就是如何将该问题划分成子问题？ 网格对应的坐标轴是什么？
② 单元格中的值需要添什么？单元格中的值通常就是你要优化的值。 如背包问题中，单元格的值就是商品的价值。

经典问题2——最长公共子序列

给两个字符串，求它们的最长公共子序列。详细题干点击这里。

该问题我们可以把它分解成求这两个字符串子串的最长公共子序列求解。
如：求 "fosh"和"fish"的最长公共子序列，我们可以先求"f"和"f"的最长公共子序列，再求"fo"和"f"的最长公共子序列，以此类推，下一个问题都是在上一个问题的解的基础上再求解，所以网格如下图所示：

得到网格后，我们就尝试往逐步向网格中添加数据，从而推导出每个网格的计算公式，最终网格结果如下。

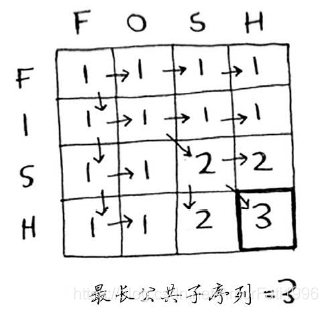
在添加数据时同步分析每个网格的计算公式，我们可以得到如下的公式。

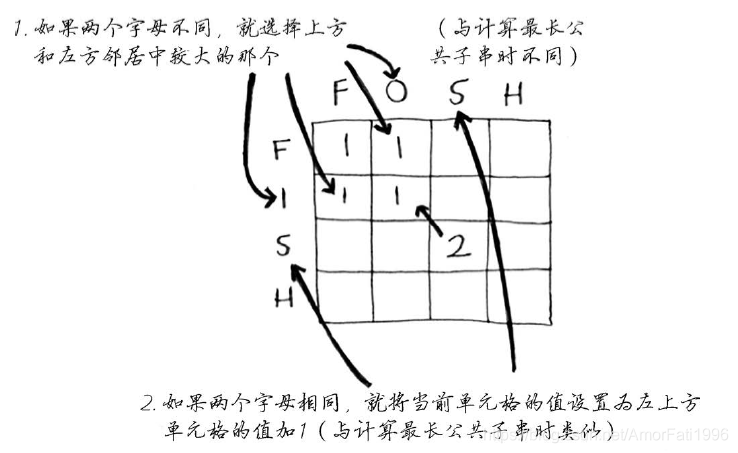
代码如下：

public class LongestCommonSubsequence {
    
    
    public int longestCommonSubsequence(String text1, String text2) {
    
    
        //为了方便计算，网格分别再第一行和第一列前插入空行和空列
        int[][] grid = new int[text1.length() + 1][text2.length() + 1];
        //因此，此处从1开始
        for (int i = 1; i < grid.length; i++) {
    
    
            for (int j = 1; j < grid[i].length; j++) {
    
    
                //此处访问text中的值要减1
                if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
    
    
                    grid[i][j] = grid[i-1][j-1] + 1;
                } else {
    
    
                    grid[i][j] = Math.max(grid[i - 1][j], grid[i][j - 1]);
                }
            }
        }
        //返回最终结果
        return grid[text1.length()][text2.length()];
    }

    //测试代码
    public static void main(String[] args) {
    
    
        System.out.println(new LongestCommonSubsequence().longestCommonSubsequence("fosh", "fish"));
    }
}

参考：《算法图解》第9章 动态规划