- 动态规划,简称DP
- 是求解最优化问题的一种常用策略
- 通常的使用套路(一步一步优化)
- 暴力递归(自顶向下,出现了重叠子问题)
- 记忆化搜索(自顶向下)
- 递推(自底向上)
动态规划的常规步骤
- 动态规划中的“动态”可以理解为是“会变化的状态”
- 定义状态(状态是原问题、子问题的解)
比如:定义dp(i)的含义 - 设置初始状态(边界)
比如设置dp(0)的值 - 确定状态转移方程
比如确定dp(i)和dp(i - 1)的关系
动态规划的一些相关概念
- 将复杂的原问题拆解成若干个简单的子问题
- 每个子问题仅仅解决1次,并保存它们的解
- 最后推导出原问题的解
- 可以用动态规划来解决的问题,通常具备2个特点
- 最优子结构(最优化原理):通过求解子问题的最优解,可以获得原问题的最优解
- 无后效性
某阶段的状态一旦确定,则此后过程的演变不再受此前各状态及决策的影响(未来与过去无关)
在推导后面阶段的状态时,只关心前面阶段的具体状态值,不关心这个状态是怎么一步步推导出来的
无后效性
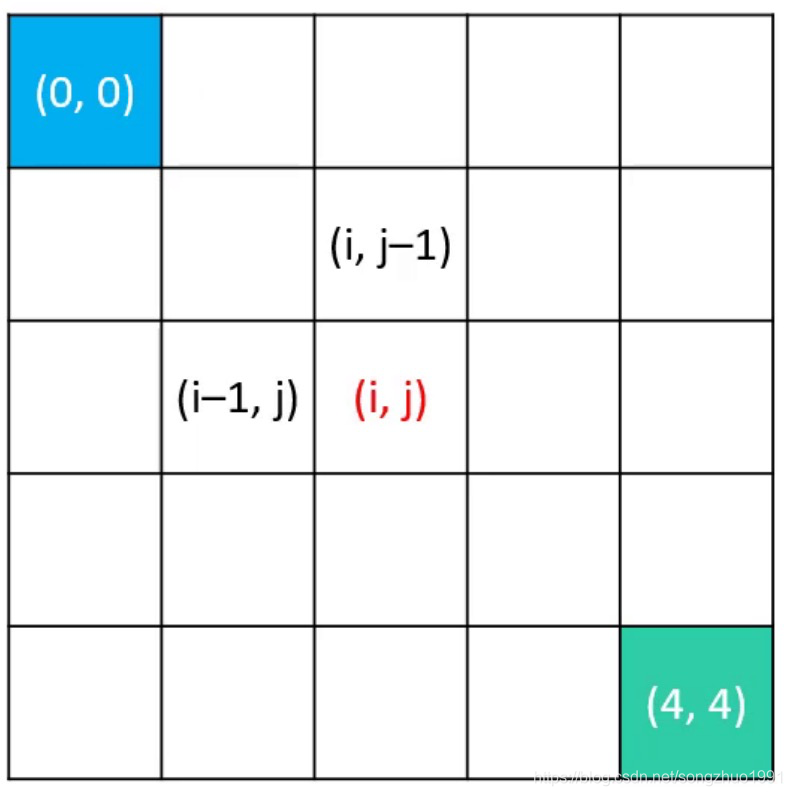
- 从起点(0, 0)走到终点(4, 4)一共有多少种走法?只能向右、向下走
- 假设dp(i, j)是从(0, 0)走到(i, j)的走法
dp(i, 0) = dp(0, j) = 1
dp(i, j) = dp(i, j - 1) + dp(i - 1, j) - 无后效性
推导dp(i, j)时只需要用到dp(i, j - 1)、dp(i - 1, j)的值
不需要关心dp(i, j - 1)、dp(i - 1, j)的值是怎么求来的
有后效性
- 如果可以向左、向右、向上、向下走,并且同一个格子不能走2次
- 有后效性
dp(i, j)下一步要这么走,还要关心上一步是怎么来的
也就是还要关心dp(i, j - 1)、dp(i - 1, j)是怎么来的?
练习1 - 找零钱
- leetcode_322_零钱兑换
- 假设有25分、20分、5分、1分的硬币,现要找给客户41分的零钱,如何办到硬币个数最少?
此前用贪心策略得到的并非是最优解(贪心得到的解释5枚硬币) - 假设dp(n)是凑到n分需要的最少硬币个数
- 如果第1次选择了25分的硬币,那么dp(n) = dp(n - 25) + 1
- 如果第1次选择了20分的硬币,那么dp(n) = dp(n - 20) + 1
- 如果第1次选择了5分的硬币,那么dp(n) = dp(n - 5) + 1
- 如果第1次选择了1分的硬币,那么dp(n) = dp(n - 1) + 1
所以 dp(n) = min { dp(n - 25), dp(n - 20), dp(n - 5), dp(n - 1) } + 1
找零钱 - 暴力递归
int coins(int n) {
if (n < 1) return Integer.MAX_VALUE;
if (n == 1 || n == 5 || n == 20 || n == 25) return 1;
int min1 = Math.min(coins(n - 1), coins(n - 5));
int min2 = Math.min(coins(n - 20), coins(n - 25));
return Math.min(min1, min2) + 1;
}
- 类似于斐波那契数列的递归版,会有大量的重复计算,时间复杂度较高
找零钱 - 记忆化搜索
int coins(int n) {
if (n < 1) return -1;
int[] dp = new int[n + 1];
int[] faces = {1, 5, 20, 25};
for (int face : faces) {
if (n < face) break;
dp[face] = 1;
}
return coins(n, dp);
}
static int coins(int n, int[] dp) {
if (n < 1) return Integer.MAX_VALUE;
if (dp[n] == 0) {
int min1 = Math.min(coins(n - 25, dp), coins(n - 20, dp));
int min2 = Math.min(coins(n - 5, dp), coins(n - 1, dp));
dp[n] = Math.min(min1, min2) + 1;
}
return dp[n];
}
找零钱 - 递推
int coins(int n) {
if (n < 1) return -1;
int[] dp = new int[n + 1];
for (int i = 1; i <= n; i++) {
int min = dp[i - 1];
if (i >= 5) min = Math.min(dp[i - 5], min);
if (i >= 20) min = Math.min(dp[i - 20], min);
if (i >= 25) min = Math.min(dp[i - 25], min);
dp[i] = min + 1;
}
return dp[n];
}
- 时间复杂度、空间复杂度:O(n)
思考题:请输出找零钱的具体方案(具体是用了哪些面值的硬币)
int coins(int n) {
if (n < 1) return -1;
int[] dp = new int[n + 1];
int[] faces = new int[dp.length];
for (int i = 1; i <= n; i++) {
int min = dp[i - 1];
faces[i] = 1;
if (i >= 5 && dp[i - 5] < min) {
min = dp[i - 5];
faces[i] = 5;
}
if (i >= 20 && dp[i - 5] < min) {
min = dp[i - 5];
faces[i] = 20;
}
if (i >= 25 && dp[i - 25] < min) {
min = dp[i - 25];
faces[i] = 25;
}
dp[i] = min + 1;
}
print(faces, n);
return dp[n];
}
void print(int[] faces, int i) {
while (i > 0) {
System.out.print(face[i] + "");
i -= faces[i];
}
System.out.println();
}
找零钱 - 通用实现
int coins(int n, int[] faces) {
if (n < 1 || faces == null || faces.length == 0) return -1;
int[] dp = new int[n + 1];
for (int i = 1; i <= n; i++) {
int min = Integer.MAX_VALUE;
for (int face : faces) {
if (i < face) continue;
if (dp[i - face] < 0 || dp[i - face] >= min) continue;
min = dp[i - face];
}
if (min == Integer.MAX_VALUE) {
dp[i] = -1;
} else {
dp[i] = min + 1;
}
}
return dp[n];
}
练习2 - 最大连续子序列和
- 给定一个长度为n的整数序列,求它的最大连续子序列和
比如-2、1、-3、4、-1、2、1、-5、4的最大连续子序列和是4 + (-1) + 2 + 1 = 6 - 状态定义
假设dp(i)是以nums[i]结尾的最大连续子序列和(nums是整个序列)
- 以nums[0] -2 结尾的最大连续子序列是 -2,所以dp(0) = -2
- 以nums[1] 1 结尾的最大连续子序列是 -1,所以dp(1) = 1
- 以nums[2] -3 结尾的最大连续子序列是 1、-3,所以dp(2) = dp(1) + (-3) = -2
- 以nums[3] 4 结尾的最大连续子序列是 4,所以dp(3) = 4
- 以nums[4] -1 结尾的最大连续子序列是 4、-1,所以dp(4) = dp(3) + (-1) = 3
- 以nums[5] 2 结尾的最大连续子序列是 4、-1、2,所以dp(5) = dp(4) + 2 = 5
- 以nums[6] 1 结尾的最大连续子序列是 4、-1、2、1,所以dp(6) = dp(5) + 1 = 6
- 以nums[7] -5 结尾的最大连续子序列是 4、-1、2、1、-5,所以dp(7) = dp(6) + (-5) = 1
最大连续子序列和 - 状态转移方程和初始状态
- 状态转移方程
- 如果dp(i - 1) <= 0,那么dp(i) = nums[i]
- 如果dp(i - 1) >= 0,那么dp(i) = dp(i - 1) + nums[i]
- 初始状态
dp(0)的值是nums[0] - 最终的解
最大连续子序列和是所有dp(i)中的最大值max { dp(i) },i ∈ [0, nums.length)
最大连续子序列和 - 动态规划 - 实现
int maxSubArray(int[] nums) {
if (nums == null || nums.length == 0) return 0;
int[] dp = new int[nums.length];
int max = dp[0] = nums[0];
for (int i = 1; i < dp.length; i++) {
int prev = dp[i - 1];
if (prev > 0) {
dp[i] = prev + nums[i];
} else {
dp[i] = nums[i];
}
max = Math.max(max, dp[i]);
}
return max;
}
- 空间复杂度O(n),时间复杂度O(n)
最大连续子序列和 - 动态规划 - 优化实现
int maxSubArray(int[] nums) {
if (nums == null || nums.length == 0) return 0;
int dp = nums[0];
int max = dp;
for (int i = 1; i < nums.length; i++) {
if (dp > 0) {
dp = dp + nums[i];
} else {
dp = nums[i];
}
max = Math.max(dp, max);
}
return max;
}
- 空间复杂度:O(1),时间复杂度:O(n)
练习3 - 最长上升子序列(LIS)
- 最长上升子序列(最长递增子序列,Longest Increasing Subsequence,LIS)
- leetcode_300_最长上升子序列
- 给定一个无序的整数序列,求出它最长上升子序列的长度(要求严格上升)
比如 [10,2,2,5,1,7,101,18] 的最长上升子序列是 [2,5,7,101]、[2,5,7,18],长度是4
最长上升子序列 - 动态规划 - 状态定义 - 假设数组是nums,[10,2,2,5,1,7,101,18]
dp(i)是以nums[i]结尾的最长上升子序列的长度,i ∈ [0,nums.length)
- 以nums[0] 10结尾的最长上升子序列是10,所以dp(0) = 1
- 以nums[1] 2结尾的最长上升子序列是2,所以dp(1) = 1
- 以nums[2] 2结尾的最长上升子序列是2,所以dp(2) = 1
- 以nums[3] 5结尾的最长上升子序列是2、5,所以dp(3) = dp(1) + 1 = dp(2) + 1 = 2
- 以nums[4] 1结尾的最长上升子序列是1,所以dp(4) = 1
- 以nums[5] 7结尾的最长上升子序列是2、5、7,所以dp(5) = dp(3) + 1 = 3
- 以nums[6] 101结尾的最长上升子序列是2、5、7、101,所以dp(6) = dp(5) + 1 = 4
- 以nums[7] 18结尾的最长上升子序列是2、5、7、18,所以dp(7) = dp(5) + 1 = 4
- 最长上升子序列的长度是所有dp(i)中最大值max { dp(i) }, i ∈ [0,nums.length)
最长上升子序列 - 动态规划 - 状态转义方程
- 遍历 j ∈ [0,i)
- 当nums[i] > nums[j]
nums[i]可以接在nums[j]后面,行程一个比dp(j)更长的上升子序列,长度为dp(j) + 1
dp(i) = max { dp(i), dp(j) + 1 } - 当nums[i] <= nums[j]
nums[i]不能接在nums[j]后面,跳过此次遍历(continue) - 状态的初始值
dp(0) = 1
所有的 dp(i) 默认都初始化为1
最长上升子序列 - 动态规划 - 实现
int lengthOfLIS(int[] nums) {
if (nums == null || nums.length == 0) return 0;
int[] dp = new int[nums.length];
int max = dp[0] = 1;
for (int i = 1; i < dp.length; i++) {
dp[i] = 1;
for (int j = 0; j < i; j++ ) {
if (nums[i] <= nums[j]) continue;
dp[i] = Math.max(dp[i], dp[j] + 1);
}
max = Math.max(dp[i], max);
}
return max;
}
- 时间复杂度:O(n),时间复杂度:O(n^2)
