广义线性回归之逻辑斯谛回归（ Logistic Regression）

广义线性模型

逻辑斯谛回归概念可以认为是属于广义线性回归的范畴，但它是用来进行分类的。
线性模型的表达式为： $f(x)=w_0+w_1x_1+w_2x_2+...+w_nx_n$ ——（1）
其中，
$x_1~x_n$ 就是n个特征，作为模型的输入
$w_0~w_n$ 就是线性模型的n+1个参数
线性模型虽然简单，却拥有丰富的变化。当我们希望线性模型（1）的预测值逼近真实标记 $y$ 时，就得到了线性回归模型，把线性回归模型简写为
$y=w_0+w_1x_1+w_2x_2+...+w_nx_n=w^Tx+b$

那么可否将模型的预测值逼近 $y$ 的衍生物呢？

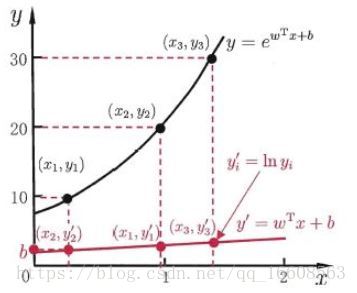
假设我们认为实例所对应的输出标记是在指数尺度上变化，那么就将输出标记的对数作为线性模型逼近的目标，
即 $lny=w^Tx+b$ ——（2）

这就是“对数线性回归”（log-linear regression）,它实际上式在试图让 $e^{w^Tx+b}$ 逼近 $y$

式2在形式上仍是线性回归，但实质上已经是在求取输入空间到输出空间的非线性函数映射。

这里的对数函数起到了将线性回归模型的预测值与真实标记联系起来的作用。（LR里面是用的sigmoid函数将线性模型的预测值与真实值联系起来的）
在这里插入图片描述
更一般地，考虑单调可微函数 $g(x)$ ,令
$y=g^{-1}(w^Tx+b)$
这样得到的模型称为“广义线性模型”（generialized linear model），其中函数 $g(x)$ 称为联系函数。
广义线性模型的参数估计通常通过加权最小二乘法或极大似然法进行求解。

逻辑斯谛回归（LR）

1.逻辑斯谛分布
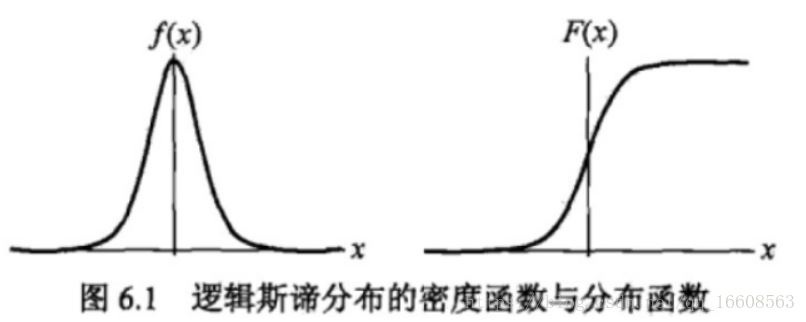
定义：设X是连续随机变量，X服从逻辑斯谛分布指的是X具有下列的分布函数与密度函数
$F(x)=P(X≤x)=\frac{1}{1+e^{-(x-μ)/γ}}$

$f(x)=F'(x)=\frac{e^{-(x-μ)/γ}}{γ(1+e^{-(x-μ)/γ})^2}$
逻辑斯谛分布的密度函数 $f(x)和分布函数F（x)的图形如下所示：$
在这里插入图片描述

2 二项逻辑斯谛回归模型

二项逻辑斯谛回归模型是一种分类模型，由条件概率分布 $P(Y|X)$ 表示，形式是参数化的逻辑斯谛分布。
定义：逻辑斯谛回归模型，二项逻辑斯谛模型是如下的条件概率分布：

$P(Y=1|x)=\frac{exp(wx+b)}{1+exp(wx+b)}$

$P(Y=0|x)=\frac{1}{1+exp(wx+b)}$
其中 w是权值向量，b是偏置，wx是w和x的内积。

对于给定的输入实例x，按照上面的公式可以求得 $P(Y=1|x)和P(Y=0|x)$ ，逻辑斯谛回归比较两个条件概率值得大小，将实例x分到概率值较大的一类。

考察逻辑斯谛回归模型的特点：
一个事件的几率（odds）是指该事件发生的概率与该事件不发生的概率的比值，如果事件发生的概率为p，那么该事件的几率为 $\frac{p}{1-p}$

该事件的对数几率为 $logit(p)=log\frac{p}{1-p}$
对逻辑斯谛回归而言

$log\frac{P(Y=1|x)}{1-P(Y=1|x)}=wx$

也就是说，在逻辑斯谛回归模型中，输出Y=1的对数几率是输入x的线性函数

3 逻辑斯谛回归如何进行分类

前面说了，对于一个给定的样本，我们只需计算下它属于每个类的概率，将它归到概率最大的那一类就行了。下面具体看下
在这里插入图片描述
深刻的理解这个图，逻辑斯谛回归才算入门了。我们来分析下

首先我们对上面的 $P(Y=1|x)=\frac{exp(wx+b)}{1+exp(wx+b)}$ 进行简单的变形，分子分母同时除以分子得到如下的形式
$P(Y=1|x)=\frac{1}{1+exp(-wx)}$ 表示样本属于1类的概率。其对应的图形就是上图所示的图形。

很明显，当取值大于0.5时，那么样本就属于1类。否则属于0类。
再来观察下， $P(Y=1|x)=\frac{1}{1+exp(-wx)}$ 样本属于1类的概率与 $wx$ 的关系，发现当 $wx$ > 0时，概率大于0.5 属于1类
当 $wx$ <0时，概率小于0.5 ，属于0类
$wx$ 就是分类边界线

我们从 $wx$ 出发，希望模型达到目标，即要尽量使训练数据中y=1的样本的 $wx$ >>0.而让y=0的样本的 $wx$ << 0

利用逻辑斯谛回归进行分类的思想就是：根据现有的数据，对分类边界线( $wx$ )建立回归公式(说白了就是求 $wx$ )，以此来进行分类。

4 逻辑斯谛回归模型参数估计（w求解）

回想下线性回归的时候，我们是如何求解权重向量w的？

说先定义损失函数为均方误差，然后求导或者使用梯度下降法对不对？
但我们在看教材的时候发现，无论是在李航的统计学习方法还是在周志华的西瓜书里面都没有直接定义损失函数，而是通过极大似然法进行参数估计的，这是为什么呢？

其实我们可以这样理解：
实质上，在这个问题里，对数损失（逻辑斯谛回归的损失函数形式上是一个对数损失，后面介绍吧）和极大似然估计是等价的
1）我们知道损失函数时用来衡量预测的错误程度的，机器学习的基本策略是使得经验风险最小化，也就是模型在训练上的损失最小，这是一种普适的思虑
2）而对于涉及概率的问题，极大似然估计也是使得估计错误最小的一种思路，从数学推导上来看，LR的经验风险就是极大似然估计去个对数加个负号而已
这是两种思维方式，但本质上是一样的，损失函数这一套逻辑是机器学习的普适逻辑，而极大似然估计这套思想是来解决概率相关问题

对数损失函数 $L(Y,P(Y|X))=-logP(Y|X)$
在逻辑斯谛回归中，其对数损失在单个样本点上的定义为

$cost(y,p(y|x))=-ylnp(y|x)-(1-y)lnp(1-(y|x))$

其中对某个具体的样本时，y要么是1要么是0
全体样本的损失函数可表达为：

$cost(y,p(y|x))=-\displaystyle\sum_{i=1}^{m}[y_ilnp(y_i|x_i)+(1-y_i)ln(1-p(y_i|x_i))]$
根据损失函数最小化，利用梯度下降法求解w（如果是极大似然估计的时候要对似然函数求最大值，用的是梯度上升法求的w，这不矛盾，数学推导可以发现他们两个差一个负号）

极大似然法求解w：
逻辑斯谛回归模型的极大似然函数为：
在这里插入图片描述
对极大似然函数 $L(w)对w求导数$
$△w=\displaystyle\sum_{i=1}^{m}[y_i-π(x_i)]x_i$
(其实对上面的损失函数求导一样可以得到相同的 $△w$ )

Logistic回归梯度上升方法
def signoid(inx):
	return 1.0/(1+exp(-inx))
def gradAscent(dataMatIn,classLabels):
	dataMatrix=mat[dataMatIn]
	labelMat=mat(classlabels).transpose()
	m,n=shape(dataMatrix)
	alpha=0.001 # 步长
	maxCycles=500
	weights=ones((n,1))
	for k in range(maxCycles):
		h=sigmoid(dataMatreix*weights) #矩阵运算，变量h不是一个数而是一个列向量，列向量元素数等于样本数。
		error = （labelMat-h）
		weights=weights + alpha*dataMatrix.transpose()*error# 注意与上面的△w 进行对比
	return weights

5.梯度上升与随机梯度上升的比较
在这里插入图片描述

在这里插入图片描述
梯度上升算法每次在更新回归系数时，都需要遍历整个数据集，当数据大时计算的复杂度太高。
一种改进方法是一次只用一个样本点来更新回归系数。该方法称为随机梯度上升算法

随机梯度上升法
def stocGradAscent(dataMatrix,classLabels):
	m,n=shape(dataMatrix)
	aplha=0.01
	weights=ones(n)
	for i in range(m):
		h=sigmoid(sum(dataMatrix[i]*weights))
		error=classLabels[i]-h
		weights=weights+alpha*error*dataMatrix[i]
	return weights

梯度上升法中变量h和误差error都是向量，在随机梯度里面都是数值。

1）梯度下降：梯度下降就是上面的推导，要留意，在梯度下降中，对于θ的更新，所有的样本都有贡献，也就是参与调整θ.其计算得到的是一个标准梯度。因而理论上来说一次更新的幅度是比较大的。如果样本不多的情况下，当然是这样收敛的速度会更快啦
2）随机梯度下降：可以看到多了随机两个字，随机也就是说用样本中的一个例子来近似所有的样本，来调整θ，因而随机梯度下降是会带来一定的问题，因为计算得到的并不是准确的一个梯度，容易陷入到局部最优解中（ https://blog.csdn.net/shenziheng1/article/details/69792696）