机器学习 | 台大林轩田机器学习技法课程笔记2 --- Dual Support Vector Machine

原文链接： https://blog.csdn.net/red_stone1/article/details/73822768

上节课我们主要介绍了线性支持向量机（Linear Support Vector Machine）。Linear SVM的目标是找出最“胖”的分割面进行正负类的分离，方法是使用二次规划来求出分类面。本节课将从另一个方面入手，研究对偶支持向量机（Dual Support Vector Machine），尝试从新的角度计算得出分类面，推广SVM的应用范围。

1. Motivation of Dual SVM

2. Lagrange Dual SVM

3. Solving Dual SVM

4. Messages behind Dual SVM

5. 总结

1. Motivation of Dual SVM

首先，我们回顾一下，对于非线性SVM，我们通常可以使用非线性变换将变量/样本从x域转换到z域中。然后，在z域中，根据上一节课的内容，使用线性SVM解决问题即可。上一节课我们说过，使用SVM得到large-margin，减少了有效的VC Dimension，限制了模型复杂度( $E_{out} \approx E_{in}$ )；另一方面，使用特征转换，目的是让模型更复杂，减小 $E_{in}$ .所以说，非线性SVM是把这两者目的结合起来，平衡这两者的关系.那么，特征转换下，求解QP问题在z域中的维度设为 $\hat{d} + 1$ ,如果模型越复杂，则 $\hat{d} + 1$ 越大，相应求解这个QP问题也变得很困难。当 $\hat{d}$ 无限大的时候，问题将会变得难以求解，那么有没有什么办法可以解决这个问题呢？一种方法就是使SVM的求解过程不依赖 $\hat{d}$ ,这就是我们本节课所要讨论的主要内容。

比较一下，我们上一节课所讲的Original SVM二次规划问题的变量个数是 $\hat{d} + 1$ ,有N个限制条件；而本节课，我们把问题转化为对偶问题（’Equivalent’ SVM），同样是二次规划，只不过变量个数变成N个，有N+1个限制条件。这种对偶SVM的好处就是问题只跟N有关，与 $\hat{d}$ 无关，这样就不存在上文提到的当 $\hat{d}$ 无限大时难以求解的情况。

如何把问题转化为对偶问题（’Equivalent’ SVM），其中的数学推导非常复杂，本文不做详细数学论证，但是会从概念和原理上进行简单的推导。

还记得我们在《机器学习基石》课程中介绍的Regularization中，在最小化 $E_{in}$ 的过程中，也添加了限制条件： $w^Tw\leq C$ .我们的求解方法是引入拉格朗日因子λ，将有条件的最小化问题转换为无条件的最小化问题： $min E_{avg}(w) = E_{in}(w)+\frac{\lambda}{N}w^Tw$ ,最终得到的w的最优化解为：

所以，在regularization问题中，λ是已知常量，求解过程变得容易。那么，对于dual SVM问题，同样可以引入λ，将条件问题转换为非条件问题，只不过λ是未知参数，且个数是N，需要对其进行求解。

如何将条件问题转换为非条件问题？上一节课我们介绍的SVM中，目标是： $min \frac{1}{2}w^Tw$ ,条件是： $y_n(w^Tz_n+b)\geq 1,n=1,2,...,N$ .首先，我们令拉格朗日因子为 $\alpha _n$ （区别于regularization），构造一个函数：

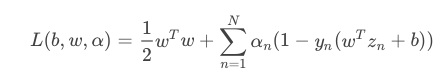
这个函数右边第一项是SVM的目标，第二项是SVM的条件和拉格朗日因子 $\alpha _n$ 的乘积。我们把这个函数称为拉格朗日函数，其中包含三个参数：b，w， $\alpha$ .

下面，我们利用拉格朗日函数，把SVM构造成一个非条件问题：

该最小化问题中包含了最大化问题，怎么解释呢？首先我们规定拉格朗日因子 $\alpha _n\geq 0$ ,根据SVM的限定条件可得： $(1-y_n(w^Tz_n+b))\leq 0$ ,如果没有达到最优解，即有不满足 $(1-y_n(w^Tz_n+b))\leq 0$ 的情况，因为 $\alpha _n\geq 0$ ，那么必然有 $\Sigma_n \alpha _n(1-y_n(w^Tz_n+b))\geq 0$ .对于这种大于零的情况，其最大值是无解的。如果对于所有的点，均满足 $(1-y_n(w^Tz_n+b))\leq 0$ ,那么必然有 $\Sigma_n \alpha _n(1-y_n(w^Tz_n+b))\leq 0$ ,则当 $\Sigma_n \alpha _n(1-y_n(w^Tz_n+b))= 0$ 时，其有最大值，最大值就是我们SVM的目标： $\frac{1}{2}w^Tw$ .因此，这种转化为非条件的SVM构造函数的形式是可行的。

2. Lagrange Dual SVM

现在，我们已经将SVM问题转化为与拉格朗日因子 $\alpha _n$ 有关的最大最小值形式。已知 $\alpha _n\geq 0$ ,那么对于任何固定的 $\alpha '$ ,且 $\alpha _n'\geq 0$ ,一定有如下不等式成立：

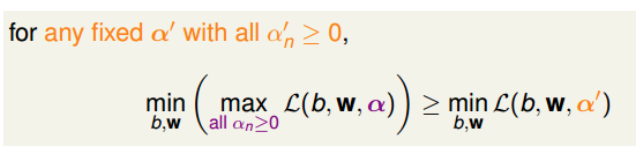
对上述不等式右边取最大值，不等式同样成立：

上述不等式表明，我们对SVM的min和max做了对调，满足这样的关系，这叫做Lagrange dual problem。不等式右边是SVM问题的下界，我们接下来的目的就是求出这个下界。

已知≥是一种弱对偶关系，在二次规划QP问题中，如果满足以下三个条件：

函数是凸的（convex primal）
函数有解（feasible primal)
条件是线性的(linear constraints)

那么，上述不等式关系就变成强对偶关系，≥变成=，即一定存在满足条件的解(b,w,α)，使等式左边和右边都成立，SVM的解就转化为右边的形式。

经过推导，SVM对偶问题的解已经转化为无条件形式：

其中，上式括号里面的是对拉格朗日函数 $L(b,w,\alpha)$ 计算最小值。那么根据梯度下降算法思想：最小值位置满足梯度为零。首先，令 $L(b,w,\alpha)$ 对参数b的梯度为零：

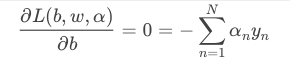
也就是说，最优解一定满足 $\Sigma_{n=1}^{N}\alpha_ny_n=0$ .那么，我们把这个条件代入计算max条件中（与 $\alpha_n\geq 0$ 同为条件),并进行化简：

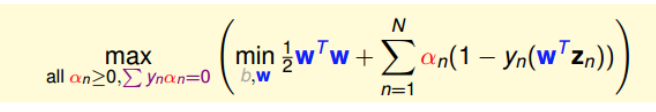
这样，SVM表达式消去了b，问题化简了一些。然后，再根据最小值思想，令 $L(b,w,\alpha)$ 对参数w的梯度为0:

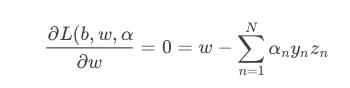
即得到：

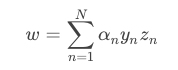
也就是说，最优解一定满足 $w = \Sigma_{n=1}^{N}\alpha_ny_nz_n$ .那么，同样我们把这个条件代入并进行化简：

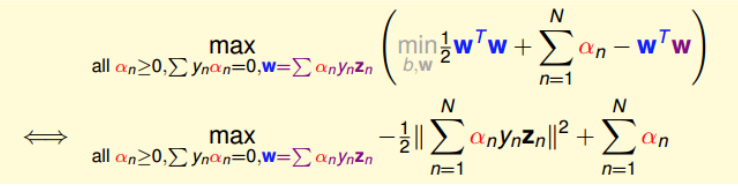
这样，SVM表达式消去了w，问题更加简化了。这时候的条件有3个：

所有 $\alpha_n\geq 0$
$\Sigma_{n=1}^{N}\alpha_ny_n=0$
$w = \Sigma_{n=1}^{N}\alpha_ny_nz_n$

SVM简化为只有 $\alpha_n$ 的最佳化问题，即计算满足上述三个条件下，函数 $-\frac{1}{2}||\Sigma_{n=1}^{N}\alpha_ny_nz_n||^2+\Sigma_{n=1}^{N}\alpha_n$ 最大值时对应的 $\alpha_n$ 是多少。

总结一下，SVM最佳化形式转化为只与 $\alpha_n$ 有关：

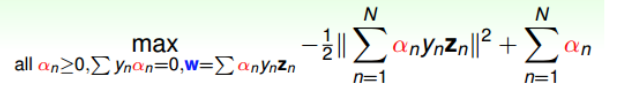
其中，满足最佳化的条件称之为Karush-Kuhn-Tucker(KKT)：

在下一部分中，我们将利用KKT条件来计算最优化问题中的α，进而得到b和w。

3. Solving Dual SVM

上面我们已经得到了dual SVM的简化版了，接下来，我们继续对它进行一些优化。首先，将max问题转化为min问题，再做一些条件整理和推导，得到：

显然，这是一个convex的QP问题，且有N个变量 $\alpha _n$ ,限制条件有N+1个。则根据上一节课讲的QP解法，找到Q，p，A，c对应的值，用软件工具包进行求解即可。

求解过程很清晰，但是值得注意的是， $q_{n,m} = y_ny_mz^T_nz_m$ ,大部分值是非零的，称为dense。当N很大的时候，例如N=30000，那么对应的 $Q_D$ 的计算量将会很大，存储空间也很大。所以一般情况下，对dual SVM问题的矩阵 $Q_D$ ,需要使用一些特殊的方法，这部分内容就不再赘述了。

得到 $\alpha _n$ 之后，再根据之前的KKT条件，就可以计算出w和b了。首先利用条件 $w = \Sigma\alpha_ny_nz_n$ （ $\alpha_n=0$ 时，点( $z_n,y_n$ )对w不起作用）,得到w，然后利用条件 $\alpha _n(1-y_n(w^Tz_n+b))=0$ ,取任一 $\alpha _n \neq0$ 即 $\alpha _n >0$ 的点，得到 $1-y_n(w^Tz_n+b)=0$ ,得到 $b = y_n-w^Tz_n$ （注意 $y_n=\pm 1$ ）.

值得注意的是，计算b值， $\alpha _n>0$ 时，有 $y_n(w^Tz_n+b)=1$ 成立。 $y_n(w^Tz_n+b)=1$ 正好表示的是该点在SVM间隔边界上，即fat boundary（是距离分类面最近的点）。也就是说，满足 $\alpha _n>0$ 的点一定落在fat boundary上，这些点就是Support Vector。这是一个非常有趣的特性。

4. Messages behind Dual SVM

回忆一下，上一节课中，我们把位于分类线边界上(间隔边界)的点称为support vector（candidates）。本节课前面介绍了 $\alpha _n>0$ 的点一定落在分类线边界（间隔边界）上，这些点称之为support vector（注意没有candidates）。也就是说分类线上的点不一定都是支持向量，但是满足 $\alpha _n>0$ 的点，一定是支持向量。

SV只由 $\alpha _n>0$ 的点决定，根据上一部分推导的w和b的计算公式，我们发现，w和b仅由SV即的 $\alpha _n>0$ 点决定，简化了计算量。这跟我们上一节课介绍的分类线只由“胖”边界上的点所决定是一个道理。也就是说，样本点可以分成两类：一类是support vectors，通过support vectors可以求得fattest hyperplane；另一类不是support vectors，对我们求得fattest hyperplane没有影响。

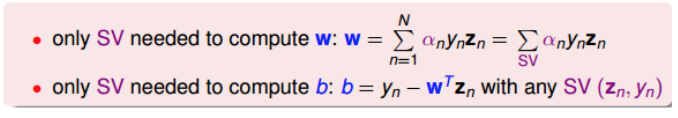
回过头来，我们来比较一下SVM和PLA的w公式：

我们发现，二者在形式上是相似的。 $w_{SVM}$ 由fattest hyperplane边界上所有的SV决定， $w_{PLA}$ 由所有当前分类错误的点决定. $w_{SVM}$ , $w_{PLA}$ 都是原始数据点 $y_nz_n$ 的线性组合形式，是原始数据的代表。

总结一下，本节课和上节课主要介绍了两种形式的SVM，一种是Primal Hard-Margin SVM，另一种是Dual Hard_Margin SVM。Primal Hard-Margin SVM有 $\hat{d}+1$ 个参数，有N个限制条件。当 $\hat{d}+1$ 很大时，求解困难。而Dual Hard_Margin SVM有N个参数，有N+1个限制条件。当数据量N很大时，也同样会增大计算难度。两种形式都能得到w和b，求得fattest hyperplane。通常情况下，如果N不是很大，一般使用Dual SVM来解决问题。

这节课提出的Dual SVM的目的是为了避免计算过程中对 $\hat{d}$ 的依赖，而只与N有关。但是，Dual SVM是否真的消除了对 $\hat{d}$ 的依赖呢？其实并没有。因为在计算 $q_{n,m} = y_ny_mz^T_nz_m$ 的过程中，由z向量引入了 $\hat{d}$ (z向量是 $\hat{d}$ 维的)，实际上复杂度已经隐藏在计算过程中了。所以，我们的目标并没有实现。下一节课我们将继续研究探讨如何消除对 $\hat{d}$ 的依赖。

5. 总结

本节课主要介绍了SVM的另一种形式：Dual SVM。我们这样做的出发点是为了移除计算过程对 $\hat{d}$ 的依赖。Dual SVM的推导过程是通过引入拉格朗日因子 $\alpha$ ，将SVM转化为新的非条件形式。然后，利用QP，得到最佳解的拉格朗日因子 $\alpha$ 。再通过KKT条件，计算得到对应的w和b。最终求得fattest hyperplane。下一节课，我们将解决Dual SVM计算过程中对 $\hat{d}$ 的依赖问题。