机器学习技法 Lecture6: Support Vector Regression

1. Kernel Ridge Regression

先回忆一下之前讲的representer理论，也就是L2正则化的线性分类模型的最佳解都能用样本点来线性表示。也就是说都能够使用核方法：

讲解正则化的时候讲过，带正则项的线性回归问题有解析解，也叫作Ridge Regression。那么使用了核方法的情况如何呢？

鞍回归的目标函数如下所示，且最优解能够使用样本点表示：

将最优解的表示代入目标函数且替换为核方法，可以得到一个新的关于系数 $\beta$的目标函数：

直接求梯度，令梯度为0，同样能够得到鞍回归的解析解：

这个解法需要 $O(N^{3})$的复杂度。不过现在利用了核方法就能够轻松地解非线性的鞍回归问题。

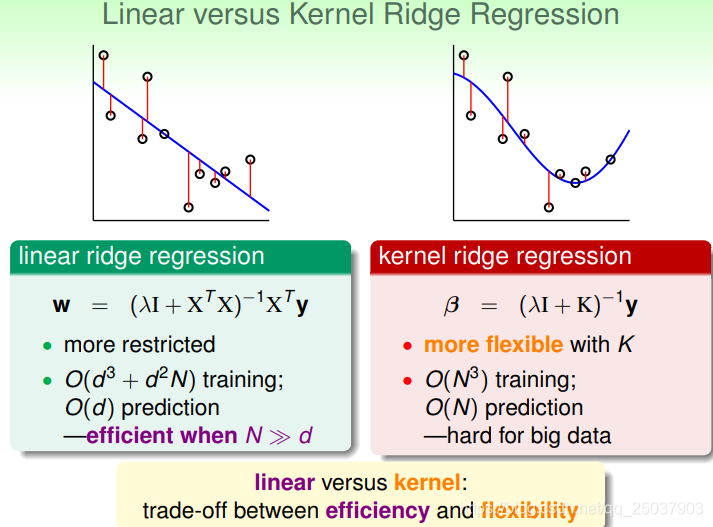
对比线性的鞍回归问题与利用了核方法的鞍回归解法，可以发现使用了核方法给问题的解决带来了灵活性，但同时也需要更复杂的计算。

2. Support Vector Regression Primal

使用了核方法的鞍回归问题也叫作最小平方SVM，简称LSSVM。对比普通的软间隔SVM与LSSVM的结果我们可以发现使用了LSSVM得到的结果虽然与SVM的结果很相近，但是LSSVM里每个点都会影响结果，大部分系数 $\beta$都是非0的，也就会导致更慢的计算。

如果我们希望能够得到一种使用核方法的回归，但是系数 $\beta$也类似软间隔SVM里比较稀疏。

可以考虑一个叫做Tube Regression的设定，那就是当样本点距离分隔面某个距离之内时，目标函数不加惩罚，超出这个距离的，乘法部分减去这个距离。

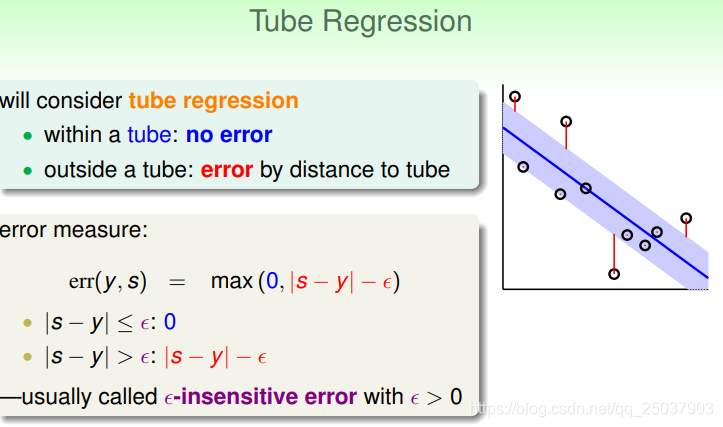
下一步就是希望在这个设定下加入L2正则化，同时得到比较系数的系数 $\beta$。可以先看一下这个问题的error与 普通线性回归的error的区别：

可以看到距离比较近的时候两个error很接近，但是错误较大时Tube Regression的error增长较慢，可能更不易收到outlier的影响。

写出加入L2正则化的目标函数：

与标准的SVM问题对比可以发现，差距主要是无法二次规划可解且不能带来稀疏的系数结果。因此我们需要改造目标函数使其接近标准SVM问题：

因为目标函数里有个绝对值项，因此需要两个松弛变量作为上下界，这样就能使目标函数接近标准SVM的形式：

最终就得到了一个同样二次规划可解的问题，叫做SVR的原始问题：

同样的，为了移除问题对于变换后的维度 $\widehat{d}$的影响，需要利用对偶问题来求解。

3. Support Vector Regression Dual

同样使用拉格朗日乘子法将限制条件代入目标函数求解，然后利用其对偶问题在满足KKT条件下的解来作为原问题的解：

整个过程和之前SVM对偶的问题里一样。我们可以对比一下得到的对偶问题的形式：

可以看到它们的形式很接近，也能够用同样的QP来解。

和软间隔SVM得到的结果相似，SVR得到的结果也有一些对松弛变量的限制条件，而这些限制条件带来了结果的稀疏性：

4. Summary of Kernel Models

在这里做一个到目前为止模型的总结。首先我们讲了几个线性模型，PLA、线性回归、逻辑回归，线性SVM和线性SVR。

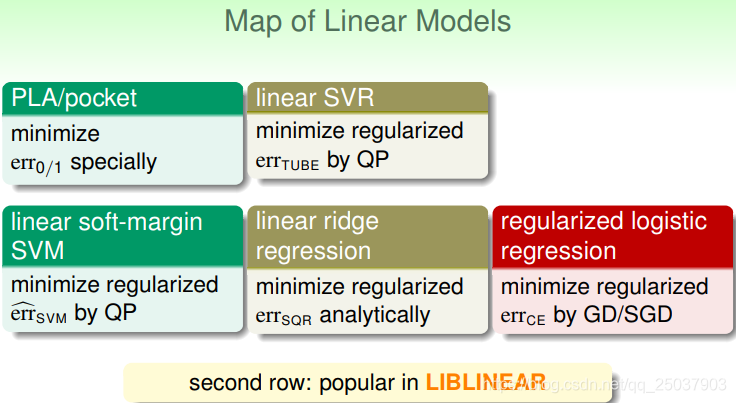
第二行的三种结果比较常用。第一行两种不常用的原因是它们需要比较大的计算量。
在线性模型的基础上使用核方法，又得到了几种非线性的模型。第四行的三种平时比较常用，第三行不常用因为它们的结果没有稀疏性：

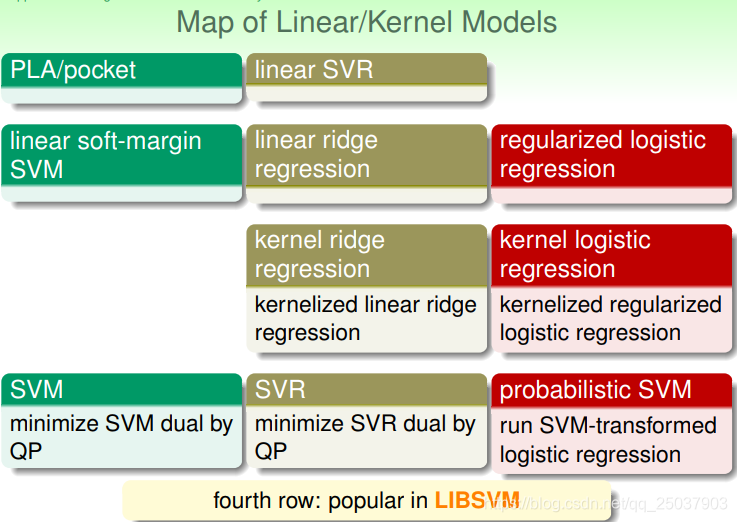
一般来说使用的核方法有多项式、高斯形式等，也可以自己定义一个核方法，但是需要满足核方法的Mercer‘s condition（也就是写为矩阵半正定，而且有对称性）。

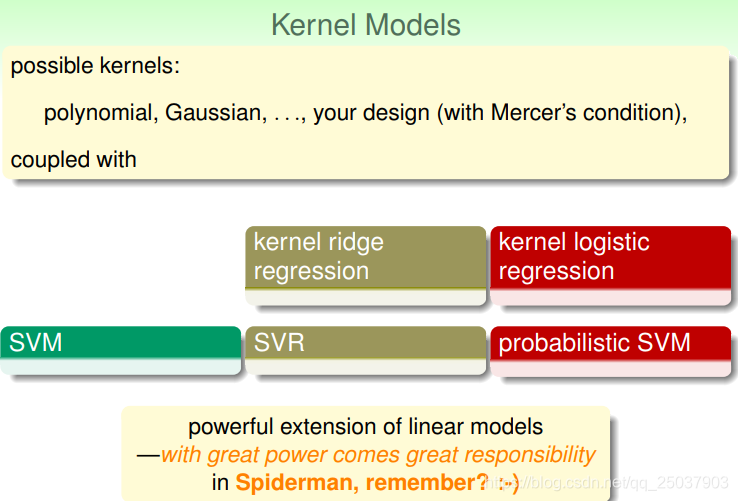
但是也要记住，使用核方法能带来更多灵活性和更强的模型同时，有可能也会带来更多的计算量，以及更容易过拟合等问题。