【莫比乌斯反演总结】

版权声明：本文为博主原创文章，未经博主允许必须转载。 https://blog.csdn.net/C20181220_xiang_m_y/article/details/84642335

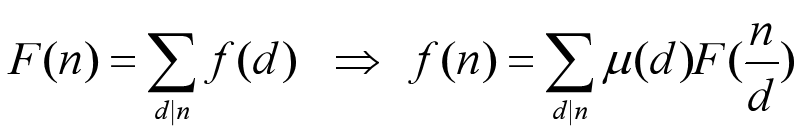
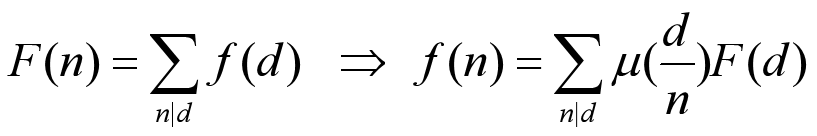
f(n)表示某一范围内(x,y)=n的数对的数量，F(n)表示某一范围内n|(x,y)的数对的数量
那么直接求f(n)并不是很好求，而F(n)求起来相对无脑一些，我们可以通过对F(n)进行莫比乌斯反演来求得f(n)
线性筛μ模板：

void Prime(int N)
{
	mu[1]=1;int cnt=0;
	for(int i=2;i<=N;i++)
	{
		if(!v[i]) p[++cnt]=i,mu[i]=-1;
		for(int j=1,k;j<=cnt&&p[j]*i<=N;j++)
		{
			v[k=p[j]*i]=1;
			if(i%p[j]==0) {mu[k]=0;break;}
			mu[k]=-mu[i];
		}
	}
}

$PS1：for(...j<=cnt...)不要漏写，会RE$

基本解题思路：枚举gcd

例题1：

求1<=i<=n, 1<=j<=m, gcd(i,j)=k 的(i,j)对数

该问题等价于求1<=i<=n/k (N), 1<=j<=m/k (M) gcd(i,j)=1 的(i,j)对数
$f(1)=\sum_{1|d}μ(\frac{d}1)*F(d)=\sum_dμ(d)*[\frac{N}d][\frac{M}d]$
由 $[\frac{N}d][\frac{M}d]$的取值是 $\sqrt{n}$级的，可以得出：

优化技巧一： 前缀和+分块优化

long long ans=0;
for(int i=1,j;i<=n;i=j+1)
{	
	j=min(n/(n/i),m/(m/i));
	ans+=1ll*(n/i)*(m/i)*(sum[j]-sum[i-1]);
}

$PS2：i=j+1不要写成i++$
$PS3:不要忘乘1ll!!!$

例题2：

求1<=i<=n, 1<=j<=m, gcd(i,j)为质数 的(i,j)对数

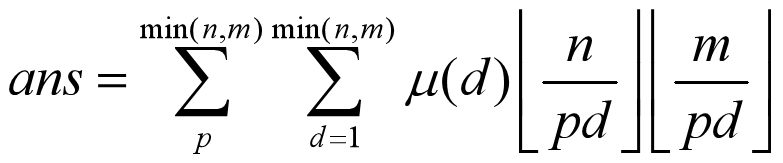
优化技巧二： 切换枚举次序

令上式的pd=T, 则有

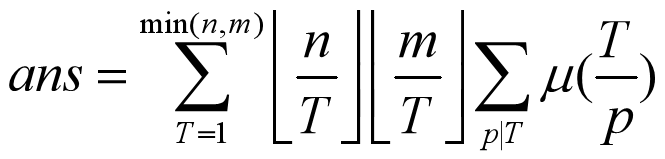
应用技巧一即可

例题3：

设 $d(x)$为 $x$的约数个数，给定N,M,T
求 $\sum_{i=1}^N\sum_{j=1}^Md(ij)$
N,M,T<=50000

题目解析见这里：约数个数和 (莫比乌斯反演)
于是算不上技巧但是很神奇的技巧三：

技巧三：替换条件框

$[(x,y)==1] &lt;=&gt;\sum_{k|(x,y)}μ(k)$

例题3 代码

#include<cstdio>
#include<algorithm>
#define maxn 50005
using namespace std;
int T,n,m,p[maxn],mu[maxn],sum[maxn],mx[maxn];//线性筛约数个数
bool v[maxn];
void Prime(int N)
{
	mu[1]=sum[1]=1;int cnt=0;
	for(int i=2;i<=N;i++)
	{
		if(!v[i]){
			p[++cnt]=i,mu[i]=-1;
			sum[i]=mx[i]=2;
		}
		for(int j=1,k;j<=cnt&&p[j]*i<=N;j++)
		{
			v[k=p[j]*i]=1;
			if(i%p[j]==0){
				mu[k]=0;
				mx[k]=mx[i]+1;
				sum[k]=sum[i]/mx[i]*mx[k];
				break;
			}
			mu[k]=-mu[i];
			mx[k]=2;
			sum[k]=sum[i]*2;
		}
	}
	for(int i=1;i<=N;i++) mu[i]+=mu[i-1],sum[i]+=sum[i-1];
}
int main()
{
	Prime(maxn-5);
	scanf("%d",&T);
	while(T--)
	{
		scanf("%d%d",&n,&m);if(n>m) swap(n,m);
		long long ans=0;
		for(int i=1,j;i<=n;i=j+1)
		{
			j=min(n/(n/i),m/(m/i));
			ans+=1ll*sum[n/i]*sum[m/i]*(mu[j]-mu[i-1]);
		}
		printf("%lld\n",ans);
	}
}