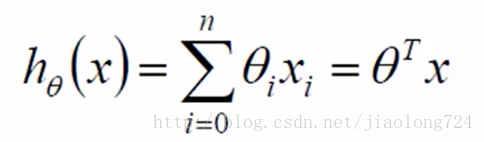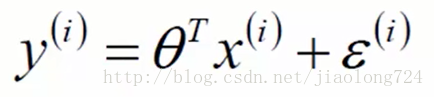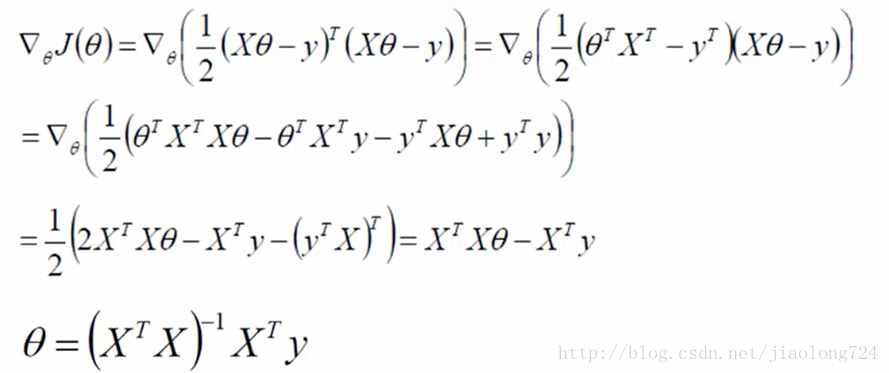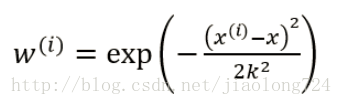前言
前面介绍了回归家族中的逻辑回归,本篇博客我们开始介绍线性回归算法相关的问题,正所谓不同的特征数据有不同的算法来对待,今天我们要研究的这个算法正好是具有线性特征的数据所具有的特征,与前面算法的一个典型特征是由于它输出为连续值,在处理这类问题时当然用线性回归算法是最好的,让我们进入正题了解这一算法的特性。
案例
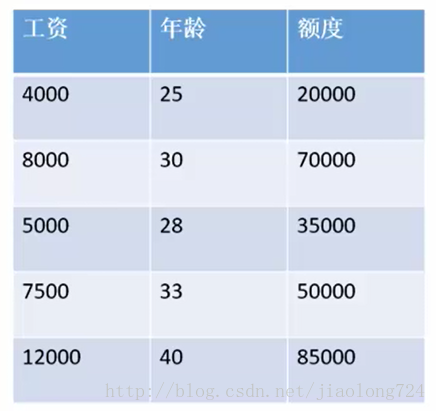
我们以一个预测一个人银行会给他带多少款的例子,银行在带给某一个人钱时并不是每个人带给的钱都一样,其中影响因素众多,比如你认识银行领导或有关系或有车房抵押那么你比别人借的钱也多,在这里我们假设只与两个因素有关,工资和年龄,如下图:
在得到上面样本数据后,我们的意图是通过已知的数据抽象、归纳也许其它一些方法得到一个模型可以预测后面其它人的贷款金额,来方便银行业务开展避免出现大的漏洞,在生成模型时 每个样本用x来表示,样本中每个特征用x1、x2表示,特征的影响程度用参数cte表示,即可得出二元一次方程如下:
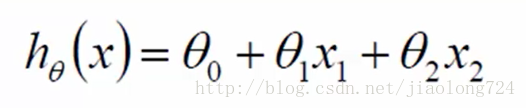
为了方便用数学中的表示方式,上面式子可以进一步化简,设x0=1,cte0*x0=cte0,并不影响结果,转化如下
上面的n表示n个特征相加,累加这里转化为了向量和逆矩阵相乘,表示为了矩阵方式 即对于一个样本的预测结果值,既然是预测结果那么值得可能性应该有三种大于真实值、等于真实值、小于真实值,这个真实值减去预测值即误差,也即真实值=预测值+误差 ,如下i表示样本的索引下标:
这里我们引入了误差的概念,假设各个样本互相独立且互相不影响,则误差服从高斯正太分布,公式如下:
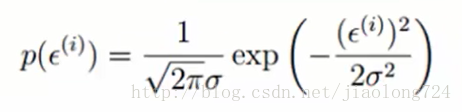
然后 误差=真实值-预测值 ,并利用最小二乘法求最大似然函数L ,推导公式如下:
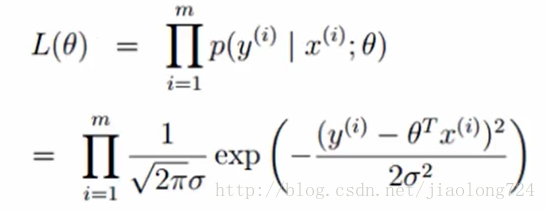
一般遇到连乘的式子,我们经常会用到取对数方式因子我们通过两边取对数方式继续分解公式,一到达到求使得函数L取的最大值的ct0值,如下:
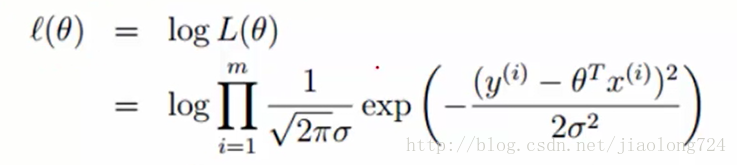
分解之后如下:
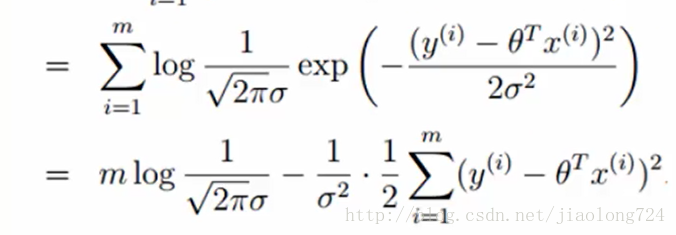
上面式子中,前面的部分是常数不会影响式子的极致,可以省略,如下:
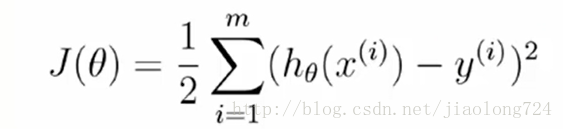
上面是化简之后的式子,需要继续求这个例子的极值,前面已经提及了h0(xi)表示预测值,yi表示真实值,这种累加符号可以转化为矩阵想成,进而对矩阵求导的思路求极值,如下
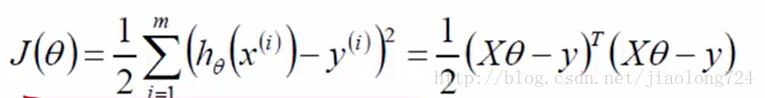
求导过程可以参考如下链接:求导公式
https://en.wikipedia.org/wiki/Matrix_calculus#Scalar-by-vector_identities
代码
如下代码是实现了上面最终推导出来的矩阵式子,其中大X表示样本矩阵,实现思路和式子如下:
def loadDataSet(filename):
'''
:param filename:路径文件
:return:训练样本数据集数组、训练分类标签数组
'''
# 特征个数索引
numFeat = len(open(filename).readline().split('\t'))-1
# 数组保存样本
dataMat = []
# 数组保存标签
labelMat = []
fr = open(filename)
# 循环每一个样本
for line in fr.readlines():
lineArr = []
curLine = line.strip().split('\t')
for i in range(numFeat):
lineArr.append(float(curLine[i]))
dataMat.append(lineArr)
labelMat.append(float(curLine[-1]))
return dataMat,labelMat
def standRegres(xArr,yArr):
'''
采用最小二乘法求最佳回归系数
:param xArr: 特征矩阵
:param yArr: 标签
:return:
'''
xMat = np.mat(xArr)
yMat = np.mat(yArr).T
xTx = xMat.T * xMat
# 判断矩阵是否可以求逆
if np.linalg.det(xTx) == 0.0:
print "this matrix is singular,bannot do inverse"
return
ws = xTx.I * (xMat.T * yMat)
return ws
def createGraph(xArr,yArr,ws):
xMat = np.mat(xArr)
yMat = np.mat(yArr)
# 预测值
yHat = xMat*ws
fig = plt.figure()
ax = fig.add_subplot(111)
# 绘制原始数据散点
ax.scatter(xMat[:,1].flatten().A[0],yMat.T[:,0].flatten().A[0])
xCopy= xMat.copy()
xCopy.sort(0)
yHat = xCopy * ws
ax.plot(xCopy[:,1],yHat)
# 比较相关系数
print "相关系数=%s" % np.corrcoef(yHat.T,yMat)
plt.show()
局部加权线性回归
线性回归经常会出现欠拟合现象,由于样本的规则并非全是直线,有时样本如果是曲线的预测出来将不准确,如下图样本为例说明:

为了解决这种样本现象问题,想出来一种策略,给待预测点的周围点添加权重,离待测点越近的点赋予权重越大,越远的点权重越小,这样预测出来的模型就会充分考虑到每个样本点附近点因素避免欠拟合问题产生,叫做局部加权回归
公式如下:
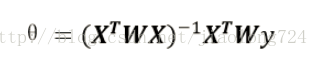
其中W称为核函数,这里使用的是高斯核 ,如下
代码实现
def lwlr(testPoint,xArr,yArr,k=1.0):
'''
:param testPoint: 测试点集
:param xArr: 特征坐标矩阵
:param yArr: 样本类别值
:param k:高斯核权重衰减系数
:return: 测试点对应的结果集 testPoint* ws
'''
# 对指定点进行局部加权回归
xMat = np.mat(xArr)
yMat = np.mat(yArr).T
m = np.shape(xMat)[0]
# 采用向量方式计算高斯核
weights = np.mat(np.eye((m)))
for j in range(m):
diffMat = testPoint - xMat[j,:]
weights[j,j] = np.exp(diffMat*diffMat.T/(-2.0*k**2))
xTx = xMat.T * (weights * xMat)
if np.linalg.det(xTx) == 0.0:
print "This matrix is singular ,cannot do inverse"
return
ws = xTx.I * (xMat.T * (weights * yMat))
return testPoint * ws
def lwlrTest(testArr,xArr,yArr,k=1.0):
'''
对指定点集进行局部加权回归
:param testArr:测试点集
:param xArr:特征矩阵
:param yArr:标签
:param k:高斯核衰减系数
:return:测试点集对应的结果集
'''
m = np.shape(testArr)[0]
yHat = np.zeros(m)
for i in range(m):
yHat[i] = lwlr(testArr[i],xArr,yArr,k)
return yHat在局部加权回归中,可以通过核函数中k值得大小来控制权重值的大小,由此来调节模型复杂度,避免产生过拟合或欠拟合问题出现。
在复杂的样本数据集中有时还会遇到样本个数小于特征数的情况,你们这种情况该如何处理呢,这时就用到了岭回归,遇到这种情况时为什么不能继续用线性或者局部加权呢,因为公式涉及到了求逆,矩阵求逆时会出错,至于为什么下面在讨论
岭回归
岭回归是在求解公式xTx后面加上 λI 使求逆部分可顺利求解,I是单位矩阵,对角线都为1看起来像一个岭,在岭回归里面一般需要数据标准化以及取不同的λ值需要多次测试和验证,具体实现请百度,还有其他的缩减系数的方法如lasso ,主要在于控制w和λ关系。
概念理解
- 方差(variance)
概率论统计学中方差用来表示随机变量的离散程度的变量,在数学中用于衡量期望的偏离程度,在实际中衡量偏离程度有实际价值,公式如下:
- 偏差
偏差又称为表观误差,是指个别测定值与测定的平均值之差,它可以用来衡量测定结果的精密度高低,在统计学中,偏差可以用于两个不同的概念,即有偏采样与有偏估计。一个有偏采样是对总样本集非平等采样,而一个有偏估计则是指高估或低估要估计的量。 - 误差
误差是测量值与真值之间的差值。用误差衡量测量结果的准确度,用偏差衡量测量结果的精密度;误差是以真实值为标准,偏差是以多次测量结果的平均值为标准。
误差与偏差的含义不同,必须加以区别。但是由于在一般情况下,真实值是不知道的(测量的目的就是为了测得真实值),因此处理实际问题时常常在尽量减小系统误差的前提下,把多次平行测量值当作真实值,把偏差当作误差。
总结
线性回归从线性角度提出了处理样本数据的理论方法,在实际问题中有很多应用场景,需要多加以思考和应用才能灵活应用,发生个人的理论还是知识都是一点点积累逐步向前发展而来,在像远方追求的同时,只有安排好时间,有一个明确的目标和时间管理才能到达始终。
题外思考
故事一则
有一对师徒,徒弟对老禅师说:“师傅,我太累,可也没见什么成就,是什么原呀?
老禅师沉思了片刻,说:“你把平常化缘的钵拿过来。小徒弟就把那个钵取来了,老禅师说:“好,把它放在这里吧,你再去给我拿几个核桃过来装满。小徒弟不知道傅的用意,捧了一堆核桃进来。这十来个核桃一放到碗里,整个碗就都装满了。
老禅师问小徒弟:“你还能拿更多的核桃往碗里放吗?拿不了了,这碗眼看已经满了,再放核核桃进去就该往下滚了。师傅说’确定碗已经满了是吗?你再捧些大米过
来。小徒弟又捧来了一些大米,他沿着核桃的缝隙把大米倒进碗里,竟然又放了很多大米进去,一直放到都开始往外掉了。小徒弟才停了下来,突然间好像有所悟:“哦,原来碗刚才还没有满。“那现在满了吗?“现在满了你再去取些水来。小徒弟又去拿水,他拿了一瓢水往碗里倒,在少半碗水倒进去之后,这次连缝隙都被填满了。老禅师问小徒弟:“这次满了吗?小徒弟看着碗满了,但却不敢回答,他不
知道师傅是不是还能放进去东西。老禅师笑着说:“你再去拿一勺盐过来。老禅师又把盐化在水里,水一点儿都没溢出去。小徒弟似有所悟。老禅师问他:’,你说这
说明了什么呢?
小和尚说:“我知道了,这说明了时间只要挤挤总是会有的。老禅师却笑着摇了摇头,说:“这并不是我想要告诉你的。接着老禅师又把碗里的那些东西倒回到了
盆里,腾出了一只空碗。老禅师缓缓地操作,边倒边说:“刚才我们先放的是核桃,现在我们倒着来,看看会怎么样?老禅师先放了一勺盐,再往里倒水,倒满之后,当再往碗里放大米的时候,水已经开始往外溢了,而当碗里装满了大米的时候,老禅师问小徒弟:“你看,现在碗里还能放得下核桃吗?
老禅师说:“如果你的生命是一只碗,当碗中全都是这些大米般细小的事情时,你的那些大核桃又怎么放得进去呢?小徒弟这次才彻底明白了。
如果您整日奔波,异常的忙碌,那么,您很有必要想一想:“我们怎样才能先将核桃装进生命当中呢?如果生命是一只碗,又该怎样区别核桃和大米呢?
如果每个人都清楚自己的核桃是什么,生活就简单轻松了。我们要把核桃先放进生命的碗里去,否则一辈子就会在大米、芝麻、水这些细小的事情当中,核桃就放不进去了。
生命是一只空碗,但是应该先放进去什么呢?什么才是你的核桃呢?
请大家思考自己的核桃大米各式什么,相信各有各的事情,如果想有所成就势必要区分哪些是自己生活中的核桃,哪些又是小米一类的事情,一个人如果想有所成就,有所事实,务必要将大的事情成为自己的主导,而不是每天为一些小米一样的事情茫茫碌碌,为生活所累,提高生活质量和生活追求。