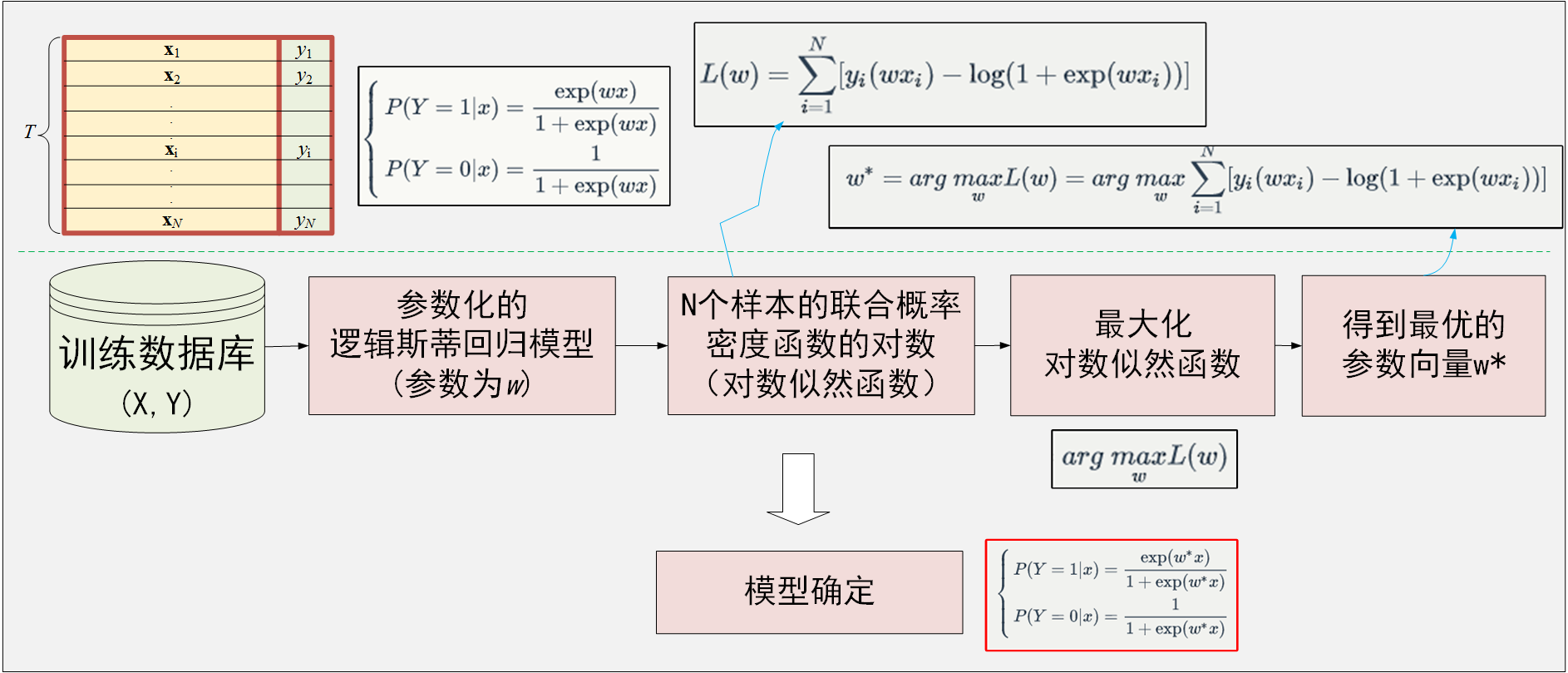
第6章 logistic regression与最大熵模型(1)·逻辑斯蒂回归模型
标签(空格分隔): 机器学习教程·李航统计学习方法
逻辑斯蒂:logistic
李航书中称之为:逻辑斯蒂回归模型
周志华书中称之为:对数几率回归模型
Andrew NG书中称之为:逻辑回归
……好吧!好多不同的名称,其实都是一种方法,晕了好久……
为了利用逻辑斯蒂分布去进行回归问题的分析,首先,必须知道什么是逻辑斯蒂分布,所以,本节主要讨论逻辑斯蒂分布,它是一个连续分布,与高斯分布非常像;
1 Logistic distribution
The Logistic distribution is a continuous probability density function that is symmetric
and uni-modal. It is similar in appearance to the Normal distribution and in practical
applications, the two distributions cannot be distinguished from one another.
1.1 一维逻辑斯蒂分布的数学定义
- 分布函数
F(x)=11+e−(x−μ)/σ
注1:也可以写成
F(x)=e(x−μ)/σe(x−μ)/σ+1
注2:分布函数(即概率累积函数)的导数
F′(x)=−(1+e−(x−μ)/σ)′(1+e−(x−μ)/σ)2=−(−1σ)e−(x−μ)/σ(1+e−(x−μ)/σ)2=1σe−(x−μ)/σ(1+e−(x−μ)/σ)2 - 概率密度函数
f(x)=1σ∗e−(x−μ)/σ(1+e−(x−μ)/σ)2
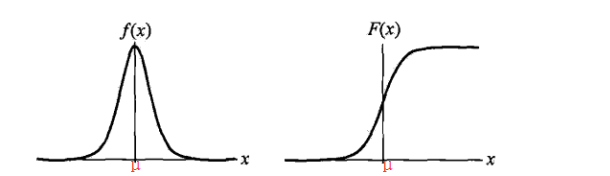
- logistic涉及两个参数
-
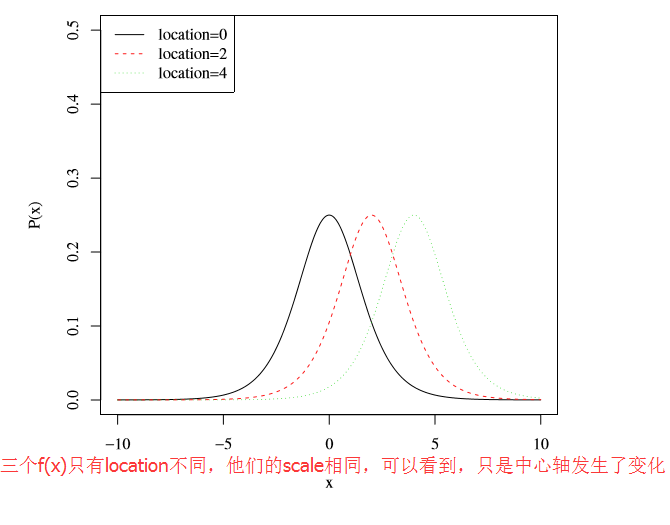
μ :location,控制分布函数的中心位置,或者说是概率密度函数对称轴的位置
-
σ :scale,该参数控制着f(x) 的宽和高;其值越大,f(x) 越矮越胖
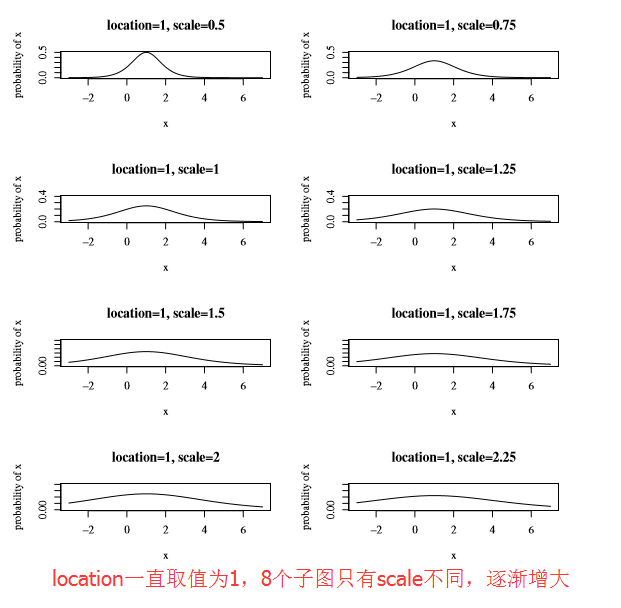
注:其实该参数σ 与正态分布的σ 含义相同,只不过相差了一个系数π23 (这个数字来自于logistic distribution的方差),
-
1.2 logistic分布的均值和方差
- 均值:
E(x)=μ - 方差:
Var(x)=13(πσ)2 - 考察高斯分布
N(μ,σ2) ,它的均值为μ ,方差为σ2 :
- 可以看到,logistic分布的方差
σ2π23 与高斯分布方差只是差了一个常数项π23 - 所以说,logistic分布与高斯分布非常相似
- 如下图所示,分别绘制出了参数为(0,1)的logistic分布和参数为(0,
π23 )的高斯分布的密度函数,此时,二者的方差取值相同(都为π23 ),可以看到,此时的logistic概率密度函数和高斯函数概率密度函数非常接近
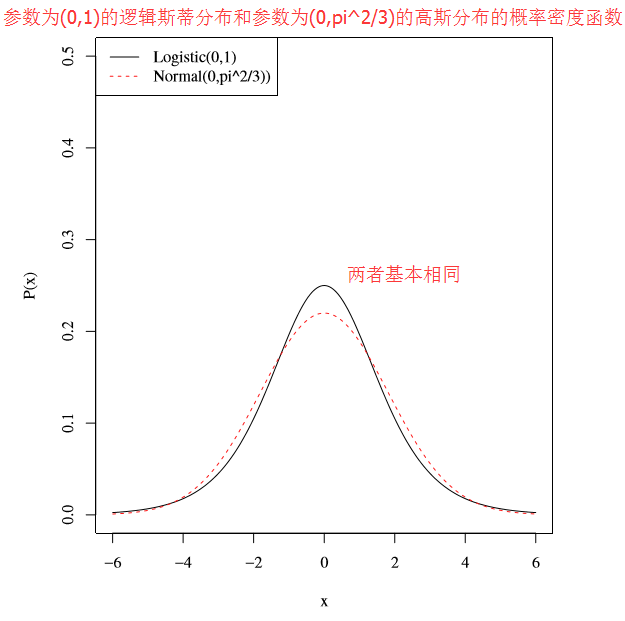
- 可以看到,logistic分布的方差
1.3 何时需要用到Logistic分布
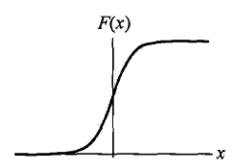
由于logistic分布的分布函数(S型)的良好的数学性质,使得它的概率密度函数具有对称性,从而,经常使用logistic分布区近似其他具有对称概率密度函数的分布
logistic分布的这种S-shapesd的分布,称为Logistic regression model,其用来对某个输入最可能的输出进行预测
logistic CDF(分布函数、cumulative distribution function)的S-shaped曲线,实际上可以描述了某一个事件发生的可能性
2. 二项逻辑斯蒂回归模型及其特点
2.1 二项逻辑斯蒂回归模型
- 上面讨论了逻辑斯蒂分布,接下来将该分布应用到机器学习的分类问题中!
- 假设我们要解决的问题为一个二分类问题,那么,可以利用逻辑斯蒂分布来对二分类模型建模,即对于一个样本x,它的类别要么为1,要么为0,我们设定它为1的概率为逻辑斯蒂分布中的概率分布形式,那么,它为0的概率也就是1-P(y=0);
- 这里的“二项”一词,与二项分布的意义相同(一次试验的结果要么为1要么为0),一个样本类别要么为1要么为0
二项逻辑斯蒂回归模型的应用场景:
两类分类问题,期Y∈{1,0}
另:样本x 具有n个特征,即x∈Rn 二项逻辑斯蒂回归模型具体形式:
⎧⎩⎨⎪⎪⎪⎪⎪⎪P(Y=1|x)=exp(w⋅x+b)1+exp(w⋅x+b)P(Y=0|x)=11+exp(w⋅x+b) - 注1:
P(Y=1|x)+P(Y=0|x)=1 - 注2:上面的二项逻辑斯蒂回归模型其实就是一个二项分布的形式,即一次试验的结果要么为1、要么为0,其中,结果为1的概率利用逻辑斯蒂分布给出
- 注1:
最终类别的判定:
对于给定的样本x ,利用二项逻辑斯蒂回归模型计算该样本类别为1和0的概率,然后,将样本x 分类到概率较大的那一类二项逻辑斯蒂回归模型的紧凑形式:对输入向量进行扩充,添加一个1,从而,可以将参数向量
w 和偏移量b 写在一起,仍记为w ,此时,逻辑回归模型为:
⎧⎩⎨⎪⎪⎪⎪⎪⎪P(Y=1|x)=exp(wx)1+exp(wx)P(Y=0|x)=11+exp(wx)
注:w⋅x+b=w1x1+⋯+wnxn+b=(w1,⋯,wn,b)T(x1,⋯,xn,1)=w∗x ,新的w∗ 仍记做w
2.2 二项逻辑斯蒂回归模型的特点
首先,给出“几率”的定义:某个事件发生的概率为
p ,那么,该事件的几率为p1−p (发生的概率与不发生的概率之比)接下来分析二项逻辑斯蒂模型中的第一项
P(Y=1|x)=exp(wx)1+exp(wx) - 经分析发现:
P(Y=1|x)1−P(Y=1|x)=ewx ,则有:log(P(Y=1|x)1−P(Y=1|x))=wx
其中,log(P(Y=1|x)1−P(Y=1|x)) 称为对数几率 - 也就是说,输出Y=1对应的对数几率是由输入x的线性函数表示的模型
wx
- 经分析发现:
- 从另外一个角度:对输入x的线性函数
wx 进行逻辑斯蒂函数计算,得到该样本属于Y=1的概率
3. 二项逻辑斯蒂回归模型参数的估计
经过前面分析可以看到,二项逻辑斯蒂回归模型具体形式为:
该模型具有一个位置的参数向量
- 对于某一个输入样本
x ,它的类别为y ,那么,它取得y 的概率到底为多大呢?根据逻辑斯蒂回归模型的定义,这个概率与y的具体取值有关:
⎧⎩⎨⎪⎪⎪⎪⎪⎪y=1时,p=exp(wx)1+exp(wx)⇒π(x)y=0时,p=11+exp(wx)⇒1−π(x) - 上式可以写为一个紧凑的形式,即
p=π(x)y⋅[1−π(x)]1−y - 即对于逻辑斯蒂回归模型而言,某个输入样本
x 对应的输出为y 的概率为p=π(x)y⋅[1−π(x)]1−y - 基于极大似然估计的思想:给定
N 个样本,最优的参数应该是使得这给定的N 个样本的联合概率密度∏Ni=1pi (即似然函数)取得最大的参数w^*,即
w∗=argmaxw∏i=1Npi=argmaxw∏i=1Nπ(xi)yi⋅[1−π(xi)]1−yi - 具体实现中,不直接最大化
N 个样本的似然函数,而是利用对数似然函数的最大化
w∗=argmaxwlog(∏i=1Npi)
其中,
L(w)=log(∏i=1Npi)=∑i=1Nlogpi=∑i=1Nlog(π(xi)yi⋅[1−π(xi)]1−yi)=∑i=1Nyilogπ(xi)+(1−yi)log[1−π(xi)]=∑i=1Nyilog(π(xi))−yilog(1−π(xi))+log(1−π(xi))=∑i=1Nyilog(π(xi)1−π(xi))+log(1−π(xi))
再将π(x) 代入,可以得到
L(w)=∑i=1N[yi(wxi)−log(1+exp(wxi))] - 最终
w∗=argmaxwL(w)=argmaxw∑i=1N[yi(wxi)−log(1+exp(wxi))] - 得到的最终模型即为
⎧⎩⎨⎪⎪⎪⎪⎪⎪P(Y=1|x)=exp(w∗x)1+exp(w∗x)P(Y=0|x)=11+exp(w∗x)
4 多项逻辑斯蒂回归
二项逻辑斯蒂回归模型用于且仅能用于2类分类问题,如果是多类分类问题,需要对二项逻辑斯蒂回归模型进行拓展,得到多项逻辑斯蒂回归模型
- 对于某一个输入样本
x ,它的输出类别的取值可能有多个(K个),此时,不能再用二项分布来描述这种分布了,而是需要利用多项式分布来描述类别的分布 - 取得每一个类别的概率还是以逻辑斯蒂分布的形式描述
- 即
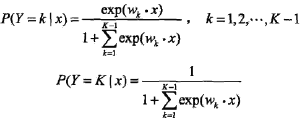
5 二项逻辑斯蒂回归和多项逻辑斯蒂回归
- 二项逻辑斯蒂回归:它可能的取值为二项分布(0-1)分布,取得每一个数值的概率可以利用逻辑斯蒂分布表示
| 可能的取值 | 1 | 0 |
|---|---|---|
| 概率 |
|
|
| 解释 | 逻辑斯蒂分布函数的形式 | 1- 逻辑斯蒂分布函数的形式 |
- 多项逻辑斯蒂回归:它可能的取值为多项式分布,取得每一个数值的概率可以利用逻辑斯蒂分布表示
| 可能的取值 | 1 | 2 | …. | K |
|---|---|---|---|---|
| 概率 |
|
|
…. |
|
| 解释 | 逻辑斯蒂分布函数的形式 | 逻辑斯蒂分布函数的形式 | …. | 1- 逻辑斯蒂分布函数的形 |
参考文献
[1] Logistic Distribution - Paul Johnson.PDF
or
[2] 统计学习方法·李航·6.1
[3] Introduction to Probability, Statistics, and Random Processes by Hossein Pishro-Nik