《算法导论》动态规划 -------python 钢条切割问题

1. 钢条切割问题：一段长为 n 的钢条和一个价格表 pi (i=1,2,3,4,...,n)，求切割方案，使得销售收益 Rn 最大。

长度 i	1	2	3	4	5	6	7	8	9	10
价格 pi	1	5	8	9	10	17	17	20	24	30

长度为 n 的钢条有 2^(n-1) 种切割方案（因为在距离钢条左端i(i=1,2,,3,...,n-1)处，我们总是可以选择切割或者不切割）

设一个最优切割方案将钢条切为 k （1≤k≤n）段，最优切割方案为：n = i1 + i2 + i3 +...+ ik

切割的长度分别为：i1、i2 、i3 、...、ik， 得到的最大收益：Rn = pi1 + pi2 + pi3 +...+ pik

2. 问题分析

首先可以将钢条分割为 i 和 n-i 两段，求这两段的最优收益 Ri 和 R(n-i) （每种方案的最优收益为两段的最优收益之和）。由于无法确定哪种方案（i 取何值时）会获得最优收益，我们必须考虑所有的i，选取其中收益最大者。若直接出售钢条会获得最大收益，可以选择不做任何切割。最优切割收益公式：Rn = max(pn,R1+Rn-1,R2+Rn-2,...,Rn-1+R1)。当完成首次切割后，我们可以将两段钢条（ i 和 n-i）看成两个独立的钢条切割问题实例，通过组合两个相关子问题的最优解，构成原问题的最优解。

一种相似但更为简单的递归求解方法：将长度为 n 的钢条分解为左边开始一段，以及剩余部分继续分解的结果。简化后的公式：Rn = max{1≤i≤n, (pi+Rn-i)}

3. 编程

方法1：自顶向下递归实现

缺点：输入规模大时，程序运行时间会变得相当长

原因：反复求解相同的子问题

#  自顶向下递归算法实现
#  R[n] = max{1≤i≤n, (pi+R[n-i])}          时间复杂度为：2^n(指数函数)
def CutRod(p, n):  # 函数返回：切割长度为 n 的钢条所得的最大收益
    if n == 0:
        return 0
    q = -1
    for i in range(1, n+1):
        q = max(q, p[i] + CutRod(p, n-i))
        '''
        tmp = p[i] + CutRod(p, n-i)
        if q < tmp:
            q = tmp
        '''
    return q
p=[0,1,5,8,9,10,17,17,20,24,30]   # 价格表，下标为对应的钢条长度，如当钢条长度为0时，p=0,即p[0]=0，p[2]=5
print("最大收益为：",CutRod(p,4))  #  最大收益为： 10

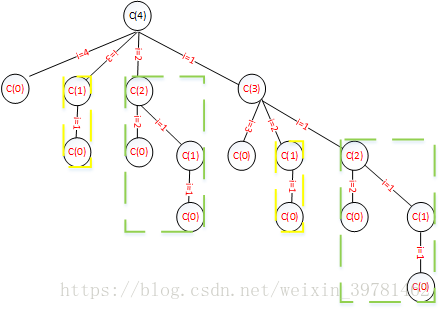
假如 n=4时，求解函数用C(4)表示，下图为 n=4 时函数的递归展开，其中被浅绿色和黄色虚线方框圈住的部分为重复的部分。其中共有2^n个结点，2^(n-1)叶节点，程序时间复杂度为2^n（指数时间复杂度）

方法2：带备忘录的自顶向下递归

特点：对每个子问题只求解一次，并将结果存储下来（随后再次遇到此问题的解，只需查找保存的结果，不必重新计算），用内存空间来节省计算时间。

# 带备忘录的自顶向下法 -- 每个子问题只求解一次，并将之存放在数组 r 中，以备用
def MemorizedCutRod(p, n):
    r=[-1]*(n+1)                          #  数组初始化
    def MemorizedCutRodAux(p, n, r):
        if r[n] >= 0:
            return r[n]
        q = -1
        if n == 0:
            q = 0
        else:
            for i in range(1, n + 1):
                q = max(q, p[i] + MemorizedCutRodAux(p, n - i, r))
        r[n] = q
        return q
    return MemorizedCutRodAux(p, n, r),r
print("最大收益为：",MemorizedCutRod(p, 5))  # 最大收益为： (13, [0, 1, 5, 8, 10, 13])

方法3：自底向上法（动态规划）

特点：任何子问题的求解都依赖于更小子问题的求解。对子问题规模进行排序，按由小到大的问题进行求解。当求解某个子问题时，他所依赖的更小的子问题都已求解完毕，结果已经保存。

优点：时间复杂度在三种方法中最好

# 自底向上
def BottomUpCutRod(p, n):
    r = [0]*(n+1)
    for i in range(1, n+1):
        if n == 0:
            return 0
        q =0
        for j in range(1, i+1):
            q = max(q, p[j]+r[i-j])
            r[i] = q
    return r[n],r
p=[0,1,5,8,9,10,17,17,20,24,30]
print(BottomUpCutRod(p, 10))   #  (30, [0, 1, 5, 8, 10, 13, 17, 18, 22, 25, 30])

《算法导论》动态规划 -------python 钢条切割问题

猜你喜欢