本人在学习《算法导论》的过程中,对于动态规划这部分的内容不是特别理解,于是决定做一下学习与解决记录,欢迎讨论交流。
0- 动态规划问题的一般步骤
1- 刻画一个最优解的结构特征
2- 递归定义最优解的值
3- 计算最优解的值,通常采用自底向上的方法
4- 利用计算出的信息构造一个最优解
1- 问题描述
Serling 公司购买长钢条,将其切割为锻钢条出售。切割工序本身没有成本支出。公司管理层希望知道最佳的切割方案。
假定我们知道Serling公司出售一段长度为i英寸的钢条的价格为pi(i = 1, 2,…,单位为美元)。钢条的长度均为整英寸。下表给出了一个价格表的样例。
| 长度i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 价格p(i) | 1 | 5 | 8 | 9 | 10 | 17 | 17 | 20 | 24 | 30 |
2-问题分析
钢条切割问题是这样的:给定一段长度为n英寸的钢条和一个价格表p(i)(i = 1, 2,…,n),求切割钢条方案,使得销售收益rn最大。注意如果长度为n英寸的钢条价格p(n)足够大,最优解可能是完全不需要切割。
考虑n=4的情况。下图给出了4英寸钢条的所有可能切割方案,包括根本不切割的方案。从下图可以看出,将一段长度为4英寸的钢条切割为两段各长为2英寸的钢条,将产生p(2)+p(2)=5+5=10的收益,为最优解。
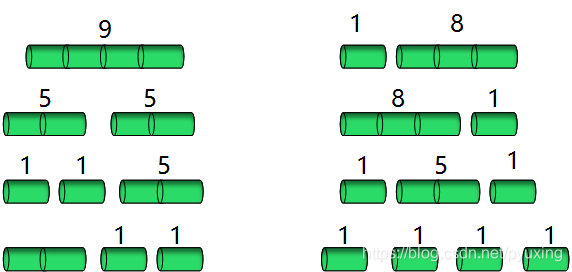
对于最优收益rn(n≥1)可以用更短的钢条的最优收益来描述:
第一个参数pn对应不切割,直接出售长度为n英寸的钢条的方案。其中n-1个参数对应另外n-1种方案:对每个i = 1, 2, …, n-1,首先将钢条切割为i和n-i的两段,接着求解这两段的最优切割收益ri和rn -i(每种方案的最优收益为两段的最优收益之和)。由于无法预知那种方案的将获得最佳收益,所以必须考虑所有可能的i,选取其中的收益最大者。如果直接出售圆钢条会获得最大收益,当然可以不做任何切割。
可以看出,通过组合两个子问题(完成首次切割之后,即将问题转化为求解两个独立的钢条切割问题实例)的最优解,并在所有可能得两段切割方案中选取组合收益最大者,构成原问题的最优解。
钢条问题是满足最优子结构的(optimal substructure) 性质的:问题的最优解由相关子问题的最优解组合而成,而且这些子问题可以独立求解。
3-自顶向下递归实现
简单的递归求解方法: 将钢条从左边切割下长度为i的一段,只对右边剩余的长度为n-i的一段继续进行切割(递归求解),对左边的一段则不再进行切割。问题的分解方式为:将长度为n的钢条分解为左边的开始一段,以及剩余部分继续分解的结果。这样,不做任何切割的方案可以描述为:第一段的长度为你n,收益为pn,剩余部分的长度为0,对应的收益r0=0。 于是可以得到如下公式:
原问题的最优解只包含一个相关子问题(右边剩余部分)的解。下面给出朴素递归算法的解:
#include <iostream>
#include <vector>
#include <limits.h>
#include <algorithm>
using namespace std;
vector<int> price{1, 5, 8, 9, 10, 17, 17, 20, 24, 30};//钢条对应的价格
int CutRod(vector<int> &price, int length){
if(length == 0) return 0;//如果钢条长度为0,直接返回
int maxvalue = INT_MIN;//因为钢条价格为正值,所以首先默认maxvalue为最小值
for(int i = 1; i <= length; ++i){
//取前一次迭代算得的maxvalue与本次迭代结果的最大值
//迭代:当前钢条段的价值 + 剩余右边钢条的价值
//(这里因为下标从0开始,所以有-1)
maxvalue = max(maxvalue, price[i - 1] + CutRod(price, length - i));
}
return maxvalue;
}
int main() {
int length = 0;
cin >> length;
cout << "maxvalue: " << CutRod(price,length)<<endl;
return 0;
}
以上利用纯迭代的方法效率很差,运行时间会呈爆炸性增长。可以取n = 4绘制递归调用树进行观察:

这棵递归调用树共有2n个结点, 其中有2n-1 个叶结点。
4-使用递归调用的方法求解钢条切割问题
动态规划有两种等价的实现方法:
1- 带备忘录的自顶向下法(top-down with memoization) :此方法仍然按照自然的递归形式编写,但过程会保存每个子问题的解。当需要一个子问题的解时,过程首先检查是否已经保存过此解。如果是,则直接返回保存的值,从而节省了计算时间;否则,按通常方式计算这个子问题。
2-自底向上法(bottom-up method):这种问题一般需要恰当定义子问题的“规模”的概念,使得任何子问题的求解都只依赖于“更小的”子问题的求解。因而我们可以将子问题按规模排序,按由小到大的顺序进行求解。当求解某个子问题时,它依赖的那些更小的子问题都已求解完毕,结果已经保存。每个子问题只需求解一次,当我们求解该问题时(第一次遇到),其所有的子问题均已求解完毕。
- 带备忘录的自顶向下法,备忘机制
#include <iostream>
#include <vector>
#include <limits.h>
#include <algorithm>
using namespace std;
vector<int> price{1, 5, 8, 9, 10, 17, 17, 20, 24, 30};//钢条对应的价格
int MemoCutRodAux(vector<int> &price,vector<int> &memoprice,int cutlength){
int maxvalue = INT_MIN;
if(memoprice[cutlength] >= 0){
return memoprice[cutlength];//入口进行检查,看所需值是否已知,如果是,则直接返回保存的值
}
if(cutlength == 0) { maxvalue = 0; }
else{
for(int j = 1; j <= cutlength; ++j){
maxvalue = max(maxvalue, price[j - 1] + MemoCutRodAux(price, memoprice, cutlength - j));
}
}
memoprice[cutlength] = maxvalue;
return memoprice[cutlength];
}
int MemoCutRod(vector<int> &price,int length){
vector<int> memoprice{};
for(int i = 0; i <= length; ++i){//特别注意的是,备忘录是包含长度为0的情况的,所以范围是[0,length]
memoprice.push_back(INT_MIN);//已知收益非负,所以可以这样处理“未知值”
}
return MemoCutRodAux(price,memoprice,length);
}
int main() {
int length = 0;
cin >> length;
cout << "MemoCutRod maxvalue: " << MemoCutRod(price,length)<<endl;
return 0;
}
- 自底向上方法:采用子问题的自然顺序,若i < j,则规模为i的子问题比规模为j的子问题“更小”,因此过程依次求解规模为j= 0, 1, …, n的子问题
#include <iostream>
#include <vector>
#include <limits.h>
#include <algorithm>
using namespace std;
vector<int> price{1, 5, 8, 9, 10, 17, 17, 20, 24, 30};//钢条对应的价格
int BottomUpCutRod(vector<int> &price, int length){
vector<int> value(length + 1);
value[0] = 0;//长度为0即没有收益
for(int j = 1; j <= length; ++j){
int maxvalue = INT_MIN;
for(int i = 1; i <= j; ++i){
maxvalue = max(maxvalue,price[i - 1] + value[j - i]);//直接访问存好的解,来获得j-i这一子问题的解,省去了递归调用
}
value[j] = maxvalue;//规模为j的子问题的解直接存入
}
return value[length];
}
int main() {
int length = 0;
cin >> length;
cout << "BottomUpCutRod maxvalue: " << BottomUpCutRod(price,length)<<endl;
return 0;
}
5-重构解
上面的解决方法中知识返回了切割问题的最优解的收益值,但并没有返回解本身(一个长度列表,给出切割后每段钢条的长度)。下面对算法进行扩展,以输出最优解的切割方案:
#include <iostream>
#include <vector>
#include <limits.h>
#include <algorithm>
using namespace std;
vector<int> price{1, 5, 8, 9, 10, 17, 17, 20, 24, 30};//钢条对应的价格
typedef struct {//结构体进行数据保存
vector<int> value{};
vector<int> cutlen{};
}stResult;
stResult ExtendedBottomUpCutRod(vector<int> &price, int length){
stResult stresult;
vector<int> valuetmp(length + 1);
vector<int> cutlentmp(length + 1);
stresult.value = valuetmp;
stresult.cutlen = cutlentmp;
stresult.value[0] = 0;
for(int j = 1; j <= length; ++j){
int maxvalue = INT_MIN;
for (int i = 1; i <= j; ++i){
if( maxvalue < price[ i -1] + stresult.value[j - i]){
maxvalue = price[ i -1] + stresult.value[j - i];
stresult.cutlen[j] = i;//保存最优切割方案
}
}
stresult.value[j] = maxvalue;
}
return stresult;
}
int main() {
int length = 0;
cin >> length;
stResult stresult = ExtendedBottomUpCutRod(price,length);
while(length > 0){
cout<<stresult.cutlen[length]<<" ";//输出最佳切割方案
length = length - stresult.cutlen[length];
}
return 0;
}
对上面的解决方案,ExtendedBottomUpCutRod(price,10)会返回如下的表格:
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| value[i] | 0 | 1 | 5 | 8 | 10 | 13 | 17 | 18 | 22 | 25 | 30 |
| cutlen[i] | 0 | 1 | 2 | 3 | 2 | 2 | 6 | 1 | 2 | 3 | 10 |
PS:公众号上线啦,技术干货分享,欢迎关注。
