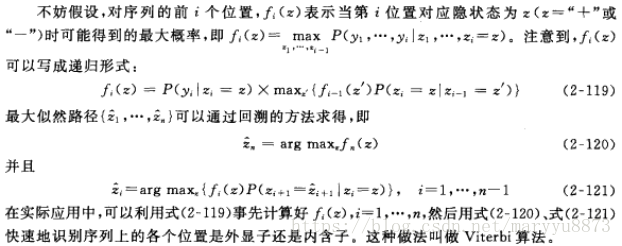浅尝马尔科夫模型

马尔科夫模型（Markov Model）又是一个我之前经常听到但从未弄明白的模型。下面我们试着来增进对它的理解。
本文将讨论在离散情况下使用马尔科夫模型的统计决策方法。
贝叶斯决策的基本思想是根据一定的概率模型得到样本属于某类的后验概率，然后根据后验概率的大小进行决策。
问题描述：基因组上CpG相对富集的区域被称作CpG岛，接下来我们要从给定的一定DNA序列，判断它是否来自CpG岛，这属于一个两分类问题。
DNA序列每个位置上的核苷酸都可以被当作一个有四种可能取值的离散随机变量 $x=\{A, T, G, C\}$。
在上述问题中我们要考虑连续位置上出现的CpG双核苷酸，可以用马尔科夫模型来表示这种相邻位置之间的依赖关系。如果第 $i$时刻上的取值依赖于且仅依赖于第 $i-1$时刻的取值，即 $P(x_i|x_{i-1},x_{i-2},...,x_1)=P(x_i|x_{i-1})$,则把这个串称作一个一阶马尔科夫链（模型）。
马尔可夫链可以用条件概率模型来描述。我们把在前一时刻某取值下当前时刻取值的条件概率称作转移概率(Transition Probability），记为 $a_{st}=P(x_i=t|x_{i-1}=s)$。
对一个长度为 $L$的序列，我们观察到这个序列的概率是： $P(x)=P(x_1,x_2,...,x_L)=P(x_1)\prod_{i=1}^na_{x_{i-1}x_i}$
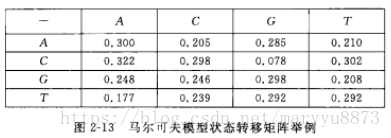
对于DNA序列来说，每一位置的取值有四种，我们把它们称作四种状态，转移概率就是一个 $4*4$的矩阵，称作转移概率矩阵或状态转移矩阵，如下图。

如果知道两类（CpG岛与非CpG岛）的状态转移矩阵，那么对于一个序列样本，我们就可以用上述公式分别计算每一类模型下观察到该特定序列的可能性或似然度 $P(x|w_i)$，用同样的类别似然比（或对数似然比）来进行类别判断。
那么怎样去确定马尔科夫状态转移矩阵（离散概率模型）呢？
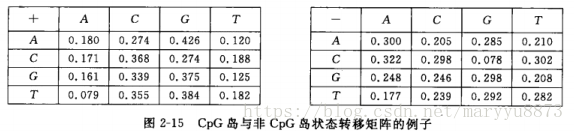
首先收集充分的、有代表性的一些CpG岛序列的片段和一些非CpG岛序列的片段，用它们构成两类训练样本。在每一类样本中，统计在所有位置上出现A、T、C、G的次数，再统计在每个A、T、C、G后面出现A、T、C、G次数，然后用 $a_{st}^+=\frac{c_{st}^+}{\sum_{t^`}c_{st^`}^+}$和 $a_{st}^-=\frac{c_{st}^-}{\sum_{t^`}c_{st^`}^-}$来分别估计两类的状态转移概率。以下给出了在某个数据集上估计的CpG岛与非CpG岛状态转移矩阵的一个例子。

对于任意一段待判别的DNA序列，可以根据状态转移矩阵计算它属于CpG岛的似然比，再通过与一定的阈值比较进行判别。
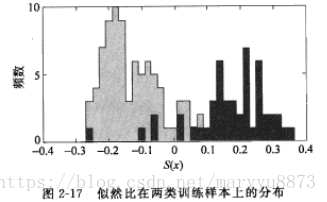
在实际应用中，人们经常通过统计所有训练样本的似然比取值的分布来确定阈值。选用不同的阈值来做决策就好导致不同的错误情况，人们可以从直方图上确定满意的阈值，或者通过变动不同阈值画出ROC曲线来决定阈值选择。

咦，马尔科夫模型的应用就是这么简单？

隐马尔可夫模型

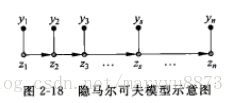
隐马尔可夫模型（hidden Markov model, HMM）是另一种常用的概率模型。在该模型中，观测是依据一定的概率由某些不可见的内部状态（隐状态）决定，而这些状态之间服从某种马尔科夫模型。以下为一个典型的HMM示意图：

其中 $y_i$是观测到的数据，它的取值根据条件概率 $f_i(y_i|z_i)$由隐状态 $z_i$决定，这一概率称作发射概率(emission probability)。同时，隐状态 $z_i$满足马尔科夫转移概率 $a_{st}=P(z_{i+1}=t|z_i=s)$

应用隐马尔可夫模型
当训练样本中的观测数据和相应的隐状态都已知时，可以根据上文给出的一般马尔科夫模型下状态转移矩阵的估计方法来估计发射概率 $f_i(y_i|z_i)$和转移概率 $a_{st}$。然而，与一般马尔科夫模型的决策过程不同，在未知数据上应用隐马尔可夫模型进行统计决策时，需要对各个观测数据点所对应的隐状态进行判断。
通过已经标注的训练样本，可以估计发射概率 $f_i(y_i|z_i)$和转移概率 $a_{st}$。对于待分析的序列 $\{y_1,...,y_n\}$，希望通过最大化概率（即似然度）P(y_1,…,y_n|z_1,…,z_n)来求得各个位置的隐状态 $\{\hat{z}_1,...,\hat{z}_n\}$，相应的解称为“最大似然路径”。
怎样求解呢？白话文版：从第一个位置开始，计算各类隐状态的最大概率，接下来依次计算在当前基础下接下来的每个位置的最大概率。

注：如无特殊说明，以上大部分内容为摘选自张学工所著《模式识别》。