随机过程:是随时间而随机变化的过程。又称为随机函数。
马尔科夫模型(VMM):它描述了一类重要的随机过程。
一个系统有有限个状态集S = {s1,s2,sN},随时间推移,该系统将同某一状态转移到另一状态。Q=(s1,s2,,,sN)为一随机变量序列,随机变量取值为状态集S中的一个状态,设时间t时状态为qt。
对系统的描述通常是给出当前时刻t的状态与其前面所有状态的关系:当前时刻 t 处于状态sj的概率取决于其在时间1,2,···,t-1时刻的状态,该概率为
P(qt = sj | qt-1 = si,qt-2 = sk ,···).
特定条件下,系统在当前时间t的状态只与t-1的状态相关,即:
P(qt = sj | qt-1 = si,qt-2 = sk ,···)= P(qt = sj | qt-1 = si),该系统构成一个离散的一阶马尔科夫链。
进一步,如果只考虑上式独立于时间t的随机过程(即与时间t的具体大小无关,亦即下面说到的状态转移矩阵不随时间变化):
P(qt = sj | qt-1 = si) = aij,1<= i,j <=N,该随机模型称为马尔可夫模型。其中状态转移概率必须满足:aij>= 0,ai1 + ai2 +...+ajN = 1 。
有N个状态的一阶马尔科夫过程有N2次状态转移,它们可以表示成一个状态转移矩阵。
马尔科夫模型可以视为一个随机的有限状态机。一个马尔科夫链的状态序列的概率可以通过状态转移矩阵上的状态转移概率计算。
隐马尔科夫模型(HMM):我们不知道模型所经过的状态序列(模型的状态转换过程是不可观察的,是隐蔽的),只知道状态的随机函数。
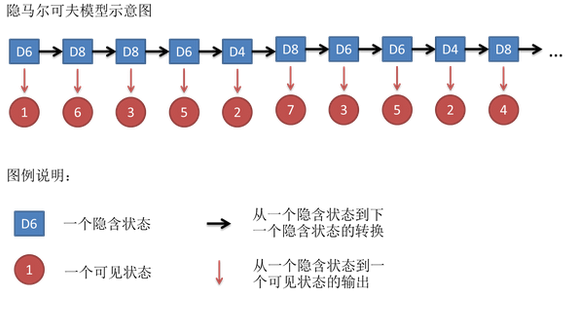
例:假定暗室中有N的口袋,每个口袋有M中不同的颜色的球。操作人员按照某一概率分布随机取一个初始口袋,从中根据不同颜色球的概率分布,随机的取出一个球,并向室外的人报告球的颜色。
然后根据口袋的概率分布选择另一个口袋,根据不同颜色球的概率分布从中随机的取出另一个球并报告颜色。重复这个过程。
该过程中,每个口袋对应HMM中的状态,从一个口袋装箱另一个口袋对应的是状态转移,从口袋中选取一个球并报告颜色对应于从一个状态中输出观察符号。
一个HMM由以下五个部分组成:
1)模型中状态的集合S,其数目N;
2)每个状态可能输出不同的符号集合K,其数目M;
3)状态转移概率矩阵A={aij}。
其中, aij = P(qt = sj | qt-1 = si) ,1<= i,j <=N,
aij>= 0,ai1 + ai2 +...+ajN = 1 。
4)从状态sj观察到符号vk的概率分布矩阵B ={bj(k)}。(观察符号的概率又称为发射概率)
其中,bj(k) = P(Ot = vk | qt = sj), 1<= j <=N 。(O = O1O2···OT,表示观察序列)
5)初始状态概率分布π = {πi}
一般一个HMM记为一个五元组μ = {S,K,A,B,π},有时简单记为三元组μ = (A,B,π)。
HMM三个基本问题:
1)估计问题:给定观察序列O = O1O2···OT和模型μ,如何快速的计算出给定模型μ情况下,观察序列O的概率,即P(O|μ)?
2)序列问题:给定观察序列O = O1O2···OT和模型μ,如何快速选择在一定意义下“最优“的状态序列Q = q1q2···qT,使得该状态序列“最好的解释”观察序列?
3)训练问题和参数估计问题:给定观察序列O = O1O2···OT,如何根据最大似然估计求模型的参数值?即如何调节模型μ的参数是的P(O|μ)最大?