隐马尔科夫模型模型：原理、实现

引入

为了更方便地理解隐马尔可夫模型，我们需要引入以下概念。

盒子模型与盒子问题（urn problem）

所谓盒子问题，就是将感兴趣的实体视为一系列的，带有颜色的球。之后，人们从盒子中取出一个或多个的球，再根据这些球，估算某些概率或概率分布。比如，估计某种颜色的球出现的概率。

所谓盒子模型，就是根据盒子问题引发而出的模型。最简单的盒子模型如下：
假设有一个盒子问题，盒子中包含两种颜色的球 $x$和 $y$，分别代表黑白，于是盒子模型有如下：

• 在置信水平 $\alpha$中从 $n$次抽样中，推断黑白颜色的球的比重。
• 在知道两种颜色的球的比重后，推断 $n$次抽样中，抽样序列出现的概率（如，抽取出一黑一白这样的序列）
• 如果 $n$次抽样中均遇到白球，那么在置信水平下，盒子中无黑色球的概率。

随机过程

随机过程可以定义为一系列于概率空间 $(\Omega ,{\mathcal {F}},P)$中的随机变量，其中 $\Omega$为采样空间， ${\mathcal {F}}$为事件空间，而 $P$为概率公理化定义。这些随机变量，都有一个索引，就像数组的下标一样。索引跟随机变量一样，其在一个度量空间 $(S,\Sigma )$中，其中 $S$为取值空间， $\Sigma$为度量空间，例如时间的时分秒、或者长度单位的连续空间，反正能够被统一的标准度量就行了。这些数学概念都比较较真，其实理解起来非常的通俗。大家可以略过。

简单来说，随机过程就是一个数组，数组中的每一个元素为随机变量，数组的索引可能不是0开始的整数序列。

用更加精确的定义，就是给定一个概率空间 $(\Omega ,{\mathcal {F}},P)$，和度量空间 $(S,\Sigma )$，然后随机过程就是一个随机变量的集合，集合中的每个元素都有索引：
${\displaystyle \{X(t):t\in T\}.}$
在历史定义中，都认为 $T$是时间序列。于是 $X(t)$就是某一个时刻 $t$的观察下，随机变量序列 $X$的取值。随机过程亦可以写成 ${\displaystyle \{X(t,\omega ):t\in T\}}$，表示随机序列 $X$的最终取值由两个变量决定，一是索引 $T$，二是抽样空间 $\omega\in\Omega$。

索引集

$T$为索引集。其通常为一个线性、一维的子集。比如自然数序列，于是通过这样的线性序列，就可以解释随机序列的实时性了。当然，索引集亦可以用笛卡尔平面，或多维平面表示，此时可以表征空间上的一个点。

状态空间

状态空间为随机变量的不同取值可能构成的空间。

采样函数

采样函数为随机过程的一种结果，其可以用如下表达：
${\displaystyle X(\cdot ,\omega ):T\rightarrow S}$

增量

随机过程的增量，可以视为随机过程通过两个采样函数后，其结果的差。如下：
${\displaystyle t_{1}\in [0,\infty )}{\displaystyle t_{1}\in [0,\infty )}$， ${\displaystyle t_{2}\in [0,\infty )}{\displaystyle t_{2}\in [0,\infty )}$，且 ${\displaystyle t_{1}\leq t_{2}}{\displaystyle t_{1}\leq t_{2}}$。于是，随机序列 $X$的增量为：
${\displaystyle X_{t_{2}}-X_{t_{1}}}$

马尔可夫链与马尔可夫过程

马尔可夫链是描述随机事件序列的随机模型。并且，每一个事件只取决于上一个事件的状态。其可以视为一个随机过程，因此也叫马尔可夫过程。如图所示：

以上是随机事件为2的马尔可夫过程，其中数字代表转换的概率。

隐马尔科夫模型定义

令 $X_n,Y_n$分别为离散时间的随机过程， $n\geq 1$。于是数对 $(X_n,Y_n)$就是一个隐马尔科夫模型，当且仅当：

• $X_n$为一个马尔可夫过程，且其不能被直接观察，是隐藏的
• ${\displaystyle \operatorname {\mathbf {P} } {\bigl (}Y_{n}\in A\ {\bigl |}\ X_{1}=x_{1},\ldots ,X_{n}=x_{n}{\bigr )}=\operatorname {\mathbf {P} } {\bigl (}Y_{n}\in A\ {\bigl |}\ X_{n}=x_{n}{\bigr )}}$
  其中， $X_n$被称为隐藏状态， ${\displaystyle \operatorname {\mathbf {P} } {\bigl (}Y_{n}\in A\ {\bigl |}\ X_{n}=x_{n}{\bigr )}}{\displaystyle \operatorname {\mathbf {P} } {\bigl (}Y_{n}\in A\ {\bigl |}\ X_{n}=x_{n}{\bigr )}}$为发射概率。

示例——帮助理解

精灵、盒子与球

假设在一个观察者不可见的房间中，有一个小精灵、若干个盒子、若干个不同标签的小球。假设盒子中包含的球都是已知的（对盒子有先验认识）。

小精灵根据某种规则，从任意一个盒子中，随机抽取出一个小球，并把他放到一个传送带中。外面的观察者通过传送带，观察到小精灵抽取出来的小球，但却不能观察到精灵是从哪个盒子抽取出来的。另外，小精灵抽取的规则，与其上一次抽取的盒子有关，但不仅仅是（即还夹杂着某些其他因素）。

于是，让我们假设盒子为 $X_n$，而小球为 $y_n$。如图所示，小球马尔可夫序列 $X_n$是不可见的，而 $y_n$小球是可见的。因此，对于这种序列，也称之为隐马尔科夫模型序列。假设小精灵从中抽取三个小球放到传送带中，但观测者仍旧无法看出小精灵的第三个小球是从哪个盒子抽取的。然而，却可以推断出，第三个小球来源于这些盒子的概率。

天气估计

假设有两个伙伴 A 和 B，A是个超级大宅男，B是一个受习惯支配的超级单调鬼。虽然 A 喜欢宅在家里，但是他要通过 B 知道今天的天气如何。于是，每天 A 就会打电话给 B，询问 B 今天做了什么？而如是回答也是 B 的习惯之一。

已知单调鬼 B 一天只喜欢做一件事，并且无外乎这三件中的一件：散步、购物和打扫卫生。并且，每天做哪件事，取决于今天的天气。于是，B今天做了哪件事，就是可以观察到的 y，而今天的天气，对 A 来说，就是观察不到的 X。

用 Python 描述：

states = ('Rainy', 'Sunny')   #假设天气只有晴雨天两种可能。
 
observations = ('walk', 'shop', 'clean')
 
start_probability = {'Rainy': 0.6, 'Sunny': 0.4}
 
transition_probability = {
   'Rainy' : {'Rainy': 0.7, 'Sunny': 0.3},
   'Sunny' : {'Rainy': 0.4, 'Sunny': 0.6},
   }
 
emission_probability = {
   'Rainy' : {'walk': 0.1, 'shop': 0.4, 'clean': 0.5},
   'Sunny' : {'walk': 0.6, 'shop': 0.3, 'clean': 0.1},
   }

表示成图像，如下所示：

其中，开始概率是 A 向 B 询问的第一天，根据他的统计得到的可能概率，或者说第一印象。因此，天气、B做的事情，就可以视为两个 随机过程，两者组成一个 隐马尔科夫模型。其中，天气为 隐马尔科夫过程。

原理描述

以下是隐马尔科夫模型的数学描述，先放上图：

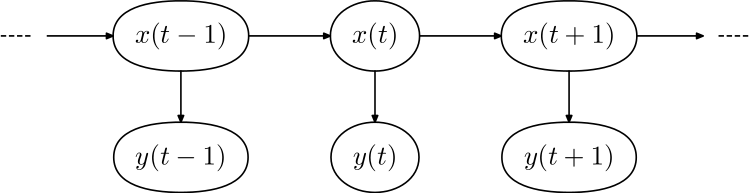
如上图所示， $x(t)$是随机变量，在时间 $t$的一个隐藏状态（不可见），比如 $x(t)\in\{ x1, x2, x3\}$。而随机变量 $y(t)$是观察变量（可见）在 $t$时的取值，比如 $y(t)\in\{ y1, y2, y3, y4 \}$。而箭头表示条件依赖。

其中， $t$时刻的随机变量 $x$，仅条件依赖于 $t-1$时刻的 $x$。同样的， $t$时刻的随机变量 $y$，仅条件依赖于 $t$时刻的 $x$。这种属性称为马尔可夫属性。

$x$的状态空间是离散的，而 $y$可以是离散的（服从范畴分布），或连续的（服从正态分布）。隐马尔科夫模型的参数有二：一是转移参数，其表示隐藏状态之间状态转换的概率，决定着 $x(t-1)$到 $x(t)$的转变。二是发射参数，其表示某个隐藏状态下，输出各个观测（y）的概率。

另外，对于转移参数，设隐藏状态 $x$的取值可能为N个。则转移参数共 $N^2$个。由于一个状态，转移到其他状态的概率和为1，故所需要求解的转移参数有 $N^2-N$个。

• 设观测变量 $y$属于离散取值，且可能取值为M个，则发射参数共 $MN$个。同样，由于概率和为1，故所需要求解的发射参数共 $N(M-1)$个。
• 若 $y$属于连续性变量，则可以用正态分布拟合它。设输出 $y$为一个向量，向量的长度为M。于是，所需要求解的正态分布的参数为M个均值、以及 ${\frac {M(M+1)}{2}}$个参数的协方差。因此，所需要求解的发射参数就是 $N\left(M+{\frac {M(M+1)}{2}}\right)={\frac {NM(M+3)}{2}}=O(NM^{2})$个。

推断问题

了解以上概念后，隐马尔科夫模型有什么用呢？

估算观测序列出现的概率

给定观测序列： $Y=y(0),y(1),\dots ,y(L-1)$，求出其概率 $P(Y)=\sum _{X}P(Y\mid X)P(X)$，其中累加遍历所有的 $X=x(0),x(1),\dots ,x(L-1)$。

计算隐藏变量的概率

即根据观测序列 $y(1),\dots ,y(t)$，计算变量（一个或多个） $x$

过滤问题

计算 $P(x(t)\ |\ y(1),\dots ,y(t))$，而 $x(t-1),x(t-2),\dots,x(0)$均未知。通常采用前向算法计算出。

平滑问题

平滑问题与过滤类似，其不是计算终端隐藏变量，而是计算序列中间的隐藏变量。即 $P(x(k)\ |\ y(1),\dots ,y(t))$其中 ${\displaystyle k<t}$

最可能解释问题

最可能即使计算的是隐藏变量序列的出现的联合概率。一般用在诸如序列标注的问题上。比如给定一些词汇，然后判断每个词汇的词性。

如上所示，已知观测序列如上。如是可以获得几个候选序列：
5 3 2 5 3 2
4 3 2 5 3 2
3 1 2 5 3 2
于是，我们可以从这些序列的联合概率中，找到最优可能的序列。这类问题一般可以用维特比算法解决。

维特比算法

维特比算法是一种动态规划算法，其从第一步开始，逐步计算。

$\sigma_t(i)$表示第 $i$号状态的时候，找到发射序列出现的联合概率的最大值。

$\sigma_{t+1}(i)=\sigma_t(j)a_{ji}b_{iq_{t+1}}$ 表示i个状态下，观测到对应的状态 $q_{t1}$的概率。

下面看个例子来深入理解这个公式。

模型训练

模型训练的过程，其实就是根据数据集（序列数据），来学习隐马尔科夫模型的参数
若训练数据中包含观测序列和隐藏序列，直接利用大数定理的结论**“频率的极限是概率”**，直接给出HMM的参数估计；

$|S_i|$ : $S_i$的个数，表示状态i的总个数。
$\sum|S_i|$：表示所有时间点上的状态个数。
如下图所示：

若训练数据中只有观测序列，则HMM的学习问题需要使用EM算法，属于非监督算法；此时一般使用Baum-Welch算法。
此时要设置一个风险函数 $L$，极大化L函数，分别可以求得π、a、b的值。这里不再介绍。

实现

综上，隐马尔科夫模型（以下称为HMM）用于解决下面三个问题：

• 根据模型参数和观测序列，找出最优可能的隐藏序列
• 根据模型参数以及观测数据，计算likelihood（概率）
• 根据观测数据，计算模型参数（训练）

搭建一个 HMM 并产生数据集

搭建y属于正态分布的HMM

import numpy as np
from hmmlearn import hmm
np.random.seed(42)

model = hmm.GaussianHMM(n_components=3, covariance_type="full")    #隐藏变量的取值总数为3个，y服从正态分布
model.startprob_ = np.array([0.6, 0.3, 0.1])    #初始概率
model.transmat_ = np.array([[0.7, 0.2, 0.1],     #转移参数
                             [0.3, 0.5, 0.2],
                            [0.3, 0.3, 0.4]])
model.means_ = np.array([[0.0, 0.0], [3.0, -3.0], [5.0, 10.0]])    #发射参数
model.covars_ = np.tile(np.identity(2), (3, 1, 1))
Y,X = model.sample(100)    #其中X为隐藏序列、Y为标注序列

运行上述代码，生成的数据集如下：
Y：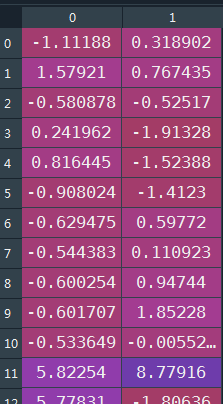
X：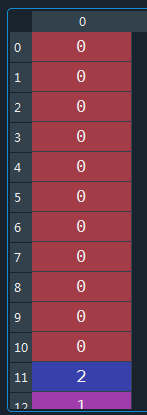

定义一个HMM，y属于离散变量的情况

status = ['盒子1', '盒子2', '盒子3']
obs = ['白球', '黑球']
n_status = len(status)
m_obs = len(obs)
start_probability = np.array([0.2, 0.5, 0.3])
transition_probability = np.array([
    [0.5, 0.4, 0.1],
    [0.2, 0.2, 0.6],
    [0.2, 0.5, 0.3]
])
emission_probalitity = np.array([
    [0.4, 0.6],
    [0.8, 0.2],
    [0.5, 0.5]
])
model = hmm.MultinomialHMM(n_components=n_status)
model.startprob_ = start_probability
model.transmat_ = transition_probability
model.emissionprob_ = emission_probalitity

se = np.array([[0, 1, 0, 0, 1]]).T    #定义一个 y 的例子，求出 X。
logprob, box_index = model.decode(se, algorithm='viterbi')
print("颜色:", end="")
print(" ".join(map(lambda t: obs[t], [0, 1, 0, 0, 1])))
print("盒子:", end="")
print(" ".join(map(lambda t: status[t], box_index)))
print("概率值:", end="")
print(np.exp(logprob)) # 这个是因为在hmmlearn底层将概率进行了对数化，防止出现乘积为0的情况

输出结果如下：

颜色:白球 黑球 白球 白球 黑球
盒子:盒子2 盒子3 盒子2 盒子2 盒子3
概率值:0.002304      （这个输出的是联合概率，是不是很小？但很遗憾，这已经是所有可能中概率最大的了）

训练一个 y 为离散的 HMM

states = ['盒子1', '盒子2', '盒子3']    #隐藏状态
obs = ['白球', '黑球']   #观测变量
n_states = len(states)
m_obs = len(obs)

model2 = hmm.MultinomialHMM(n_components=n_states, n_iter=20, tol=0.001)
X2 = np.array([
    [0, 1, 0, 0, 1],
    [0, 0, 0, 1, 1],
    [1, 1, 0, 1, 0],
    [0, 1, 0, 1, 1],
    [0, 0, 0, 1, 0]
])
model2.fit(X2)
print("输出根据数据训练出来的π")
print(model2.startprob_)
print("输出根据数据训练出来的A")
print(model2.transmat_)
print("输出根据数据训练出来的B")
print(model2.emissionprob_)