概率模型（三）：隐马尔科夫模型HMM

HMM，隐马尔科夫模型（Hidden Markov Model），是比较经典的机器学习模型，非常适合于输入是"序列"的问题的建模，包括"文本序列"、“时间序列”、"行为序列"等等，广泛的应用在语言识别，自然语言处理，模式识别等领域。

马尔科夫假设

实际问题当中，为了对观察到的序列数据进行建模分析，我们常常做这样一个假设，也就是假设当前的观察到的目标的状态仅仅与目标的前N个状态相关，这个假设被称为马尔科夫假设。

首先我们用 $V$ 表示观察到的状态的集合，即：

$V=\{v_1,v_2,...,v_M\}$

其中， $M$ 表示观察状态的数量。

比如在考虑天气问题的时候，假设每天的天气状态分为三种,即 $V = \{Sun,Cloud,Rain\}$ , 在预测未来天气问题的时候，我们完全可以假设未来某天的天气情况至于它之前的N天的天气情况相关。

符合马尔科夫假设的过程，我们称为一个马尔科夫过程。在一个马尔科夫过程中，如果当前状态仅依赖于前n个状态的话，这个过程被称为n阶马尔科夫模型。

其中最简单的一种N阶马尔科夫模型，就是当 $n=1$ 的时候，被称为一阶马尔科夫模型。也就是系统在t时刻的状态仅与时刻t-1处的状态有关，这个性质被称为无后效性，公式表达如下：

$p(o_t=v_j|o_{t-1}=v_i,o_{t-2}=v_k,...)=p(o_t=v_j|o_{t-1}=v_i)$

其中 $O=\{o_i\}$ 表示时间 $i$ 时观察到的模型状态。

对于一个马尔科夫模型，如果状态的转移概率与时间无关，则称之为齐次马尔科夫模型。例如，一阶齐次马尔科夫过程满足下列方程：

$p(o_t=v_j|o_{t-1}=v_i) = p(o_k=v_j|o_{k-1}=v_i)$

再次以天气为例，只不过这次我们加上一个限制条件，假设我们无法直接观察室外的天气情况，只能观察室内湿度情况，如此我们该如何建模这个问题呢？显然传统的马尔科夫模型就不行了，这时候我们就需要隐马尔科夫模型了。

对于隐马尔科夫模型，除了上面定义的观察状态集合 $V$ 之外，还存在一个隐藏状态集合 $Q$ :

$Q=\{q_1,q_2,...,q_N\}$

其中 $N$ 表示隐藏的状态数。

另外，HMM还假设任意时刻观察状态仅仅依赖于当前的隐藏状态，即：

$b_j(k)=P(o_t=v_k|i_t=q_j)$

这样隐藏状态到观察状态的概率构成了混淆矩阵(confuse matrix) $B$ .

具体到我们的天气问题来说，也就有：

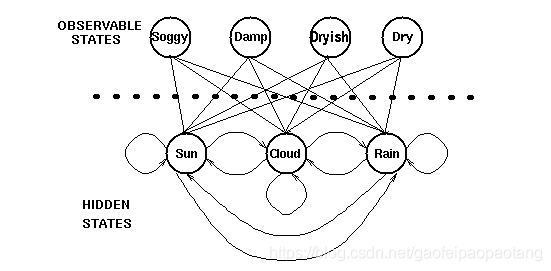
$V=\{Soggy,Damp,Dryish,Dry\}$

$Q=\{Sun,Cloud,Rain\}$

并且隐藏状态之间转化是满足马尔科夫假设，观察状态仅仅依赖于当前的隐藏状态：

在这里插入图片描述

HMM模型相关的问题有三大类：

1.计算观察序列的概率：已知模型参数，计算某一给定的可观察状态序列的概率，在给定模型 $\lambda$ 的情况下，计算 $P(O|\lambda)，O=\{o_1,o_2,...,o_T\}$ 。

2.求解隐藏状态序列: 给定模型参数 $\lambda$ 和观察序列 $O$ ,求概率最大的隐藏状态序列。

3.模型参数训练：根据观察到的序列集 $O$ 找到一个最有可能的HMM模型参数。