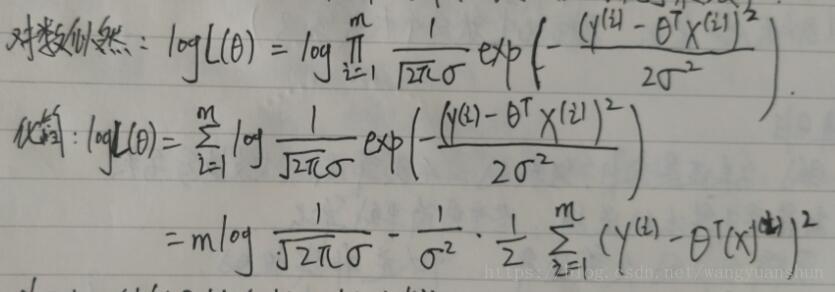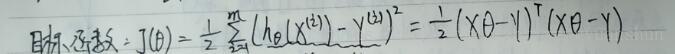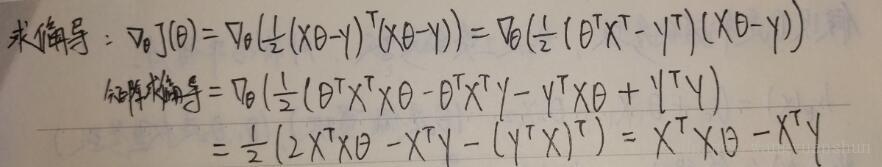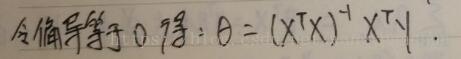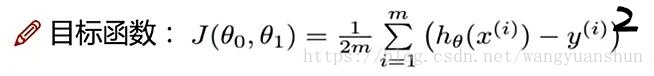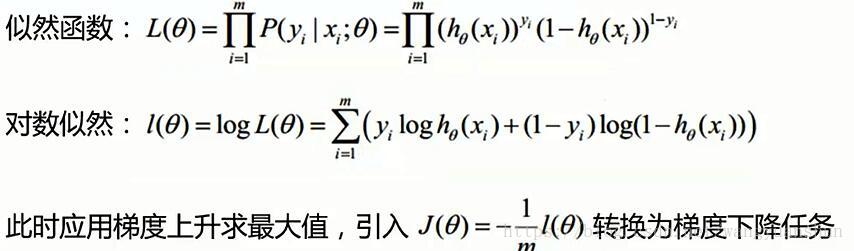线性回归算法
线性回归算法是机器学习中最基本的一个算法，但是该算法的思想、原理相当重要。本文将详细从原理上讲解线性回归算法
从一个例子引入：想象一下，假如我要去银行贷款，银行会问我两个问题，一是工资、二是年龄。根据我的回答，银行将计算出能贷多少给我。
目标：预测银行会贷给我多少钱（贷款额度），标签；是一个具体的值，属于回归问题。
数据：工资和年龄这两个特征
考虑：工资和年龄都会最终影响到贷款额度，那么工资和年龄对贷款额度的影响权重是多少？
如下表：
| x0 | 工资 x1 | 年龄 x2 | 贷款额度 y |
| 1 | 4000 | 25 | 20000 |
| 1 | 8000 | 30 | 70000 |
| 1 | 5000 | 28 | 35000 |
| 1 | 7500 | 33 | 50000 |
| 1 | 12000 | 40 | 85000 |
此表有5个样本（5行），特征x1表示工资，特征x2表示年龄，预测贷款额度y（具体数据），特征x0为方便矩阵计算而插入的数据（可以这样理解，1x任何数=任何数，只是起到占位的功能）
通俗的解释就是输入x1、x2（工资、年龄），输出银行的贷款额度y。即画出一条"线，面"来拟合我们的数据点。如下图：
如何拟合出这样一条最合适的“线，面”呢？上图中，红色点为真实值，每一个红色点到面的距离为一个误差，线段的长短表示误差的绝对值，面上或面下的红色点分别表示了误差的正负。 数学推导来了！直接上图片吧
备注：偏置项参数对结果的影响小于权重参数对结果的影响。对第三行化简得到的式子解释一下，有多少个特征x有多少个参数theta
误差，这是一个非常核心的概念，贯穿整个机器学习的过程
1000个样本就有1000个误差，10000个样本就有一万个误差，误差是独立并且有相同分布，并且都服从均值为0的高斯分布，由误差组成的矩阵为实对称矩阵，实对称矩阵的平方=该矩阵的转置x该矩阵本身。这是概率论的知识。
独立：张三和李四一起来贷款，他俩没有任何关系（独立的两个样本）。
同分布：他俩都来的是我们假定的这家银行（贷款金额计算规则一样）。
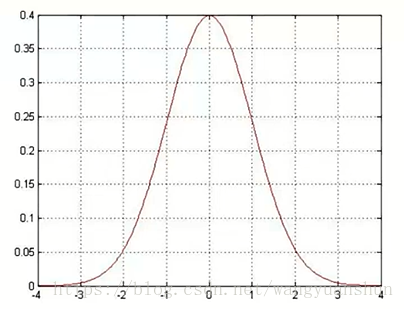
高斯分布：银行可能会多给，也可能会少给，但绝大多数情况下这个浮动不会太大，极小情况下浮动会比较大，符合正常情况。高斯分布大概长成这样：
接着上面的数学推导
似然函数：通俗讲，假设我去赌场赌博，可是我不知道我今天能不能赢钱（不知道今天赌场服从什么规则），于是我堵在赌场门口，出来一个人问一个人，总共问了10个人，有9个人都说赢钱了，1个人输了。这时我就能认为，只要我进去赌钱，90%的概率能够赢钱，赌场的规则对于每个样本是一样的。似然函数就是通过样本估计参数的值，也就是参数估计，通过观察一批样本就可以推导出赌场服从theta参数的规则。
得到如下的似然函数：
似然函数解释：什么样的参数跟我们的数据组合后恰好是真实值（样本估计参数）。
对数似然函数：计算机处理加法效率高于乘法。乘积的对数=对数的和，取对数并化简得到如下图所示：
似然函数是越大越好，对数似然函数也是越大越好，要想让对数似然越大，只需让目标函数J(Θ)越小，即：
最小二乘法相当重要，全称为最小化误差的平方和，使得拟合对象无限接近真实对象。
这里解释一个很重要的问题，为什么是平方的问题。
答：上面的推导是通过求解极大似然函数而得到了平方，下面从几何的角度直观的解释这个问题。假设有一条直线y=ax+b，要在直线上找到一个点，使得该点到定点（x0,y0）的距离最短。
1、如果用绝对值得方法寻找，也就是取min(|y-y0|+|x-x0|)，由于绝对值最小为0，所以最小的情况就是x=x0或者y=y0处，如下图所示：
2、如果采用平方和的方法寻找，就是取点到直线的垂直距离，也就是数学中最常见的数学的概念。如下图所示：
因此，相比于绝对值的方法，取平方的方法可以得到更短的距离，使得拟合函数更接近真实值。这是从范数的角度回答了这个问题，绝对值对应的范数是1，平方（最小二乘法）对应的范数是2。完美的解释了最小二乘法为什么能应用到线性回归中，知其然也知其所以然。
面试必问：1、为什么要引入似然函数？
2、为什么要对似然函数进行对数变换？
3、为什么要让目标函数越小越好？
4、为什么范数是2不是1？
接下来就是对目标函数J(Θ)的求解，什么样的Θ能使目标函数最小，解Θ。
接下来涉及到矩阵的求偏导公式，简单的有四个，如下：
Y = A * X --> DY/DX = A'
Y = X * A --> DY/DX = A
Y = A' * X * B --> DY/DX = A * B'
Y = A' * X' * B --> DY/DX = B * A'
按照公式带入求解就可得到如下图：
根据高数知识，要求最小值，只需令偏导数等于零（方程两端乘以对应的逆矩阵），即可解出Θ，如下图，矩阵X,Y已知，可得出Θ向量。
现在我们把Θ解出来得到一个三行一列的列向量(具体数据我也没带入计算)，解出了两个权重参数和一个偏置项参数
接下来谈谈这样做的不足：
1、这与机器学习本身有矛盾，机器学习应该是一个逐步求解优化的过程，而不是一下得到精确答案的过程（当然上面的解法没有错，只是线性回归是数学上的一个巧合，刚好可以解出最精确的答案，不需要一步一步迭代求解）。
2、由结果可以看出，前提得要求(X的转置乘以X)可逆，否则无法解出结果。
既然有不足（或者局限性），就需要改进，采用梯度下降的策略将很好的解决这个问题。如下
梯度下降
引入：当我们得到一个目标函数后，如何进行求解？
直接求解？（并不一定可行，线性回归可以当做是一个特例，有一定局限性）
常规套路：机器学习的套路就是交给机器一堆数据，然后告诉它沿着什么样的学习方式是对的（目标函数），让它朝着这个方向去做。
如何优化：一口吃不成个胖子，我们要静悄悄的一步步地完成迭代过程（每次优化一点点，积累起来就是大成绩了）。
现在的目标函数是（除以了样本个数m）：
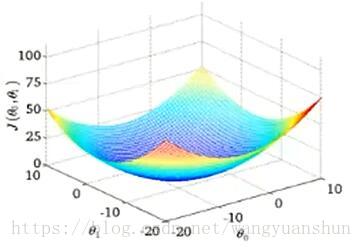
目标函数函数图像如图：
现在的目的就是寻找上图的最低点，也就是我们目标函数的终点（什么样的参数能使目标函数达到极值点）
（梯度下降）下山分几步走呢？（更新参数）
1、找到当前最合适的方向。
2、走一小步，步子走大了该“跌倒”了。
3、按照方向与步伐去更新我们的参数。
梯度下降的三种策略：批量梯度下降、随机梯度下降、小批量梯度下降。优劣如下图：
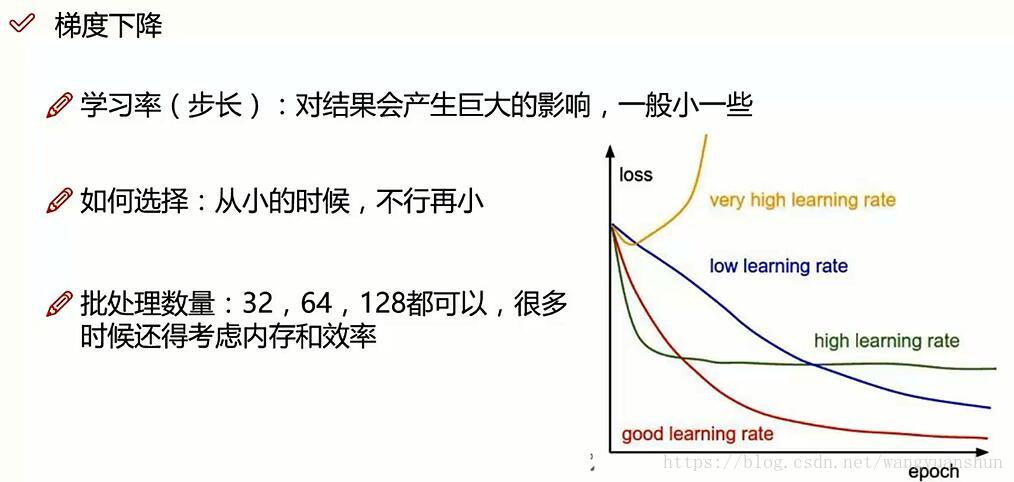
梯度下降学习率对结果的影响，如下图：
学习率初始化策略：先用0.01，不行再小，学习率可以随着迭代次数的增加而变小。
批处理数量初始化策略：一般用2的倍数，可以先用64，多大的处理量能最大满足你在时间上的容忍程度，批处理数量越大，耗时越久；同时稳定程度也越高。
逻辑回归（Logistic regression）
首先明确，逻辑回归是分类任务，是最经典、最牛x的二分类算法，也支持多分类任务。
机器学习中，分类算法的选择：先用逻辑回归，再用复杂的，能用简单的还是尽量用简单的算法，简单高效就行。
逻辑回归的决策边界：可以是非线性的。
提到逻辑回归，当然不得不讲到Sigmoid函数，如下图：
上图已经很好地解释了Sigmoid函数。
将线性回归的输入数据带入到Sigmoid函数中得到预测函数如图：
对于二分类任务，如图：
接下来和之前一样的套路，就是取似然函数，再取对数似然，此时的对数似然函数是梯度上升问题，一般都会转化为梯度下降问题。就是要想求对数似然函数的最大值，需要求目标函数的最小值（目标函数=（-1/m）*对数似然函数），如下图：
然后对目标函数J(Θ)求偏导，注意是对每一个Θj求偏导，有多少个特征就有多少个Θj。推导过程如下图，建议拿笔亲自推导一下：
综上，以上就是我对线性回归算法、逻辑回归算法的理解，希望对你有所帮助，机器学习小白，有误之处，万望谅解，喜欢博主就关注一波吧，会持续更新相关内容！