大意是两名玩家对于一个给定的日期进行变换操作,一次操作可以将其变为下一天,也可以变为下个月的同一天(若存在),达到2011年11月4日的玩家获胜,问两名玩家皆采取最优策略,先手是否必胜。
这题大概思路就是先预处理出从1900年到2001年每个月的天数,然后打表求出每一天的sg函数,最后直接调用即可。
#include<iostream>
using namespace std;
#define For(i,a,b) for(int i=a;i<=b;i++)
#define _For(i,a,b) for(int i=a;i>=b;i--)
int sg[110][15][35],mon[110][15];
int q[]={0,31,28,31,30,31,30,31,31,30,31,30,31},t;
void init(){
int tmp;
For(i,1900,2001){
For(j,1,12){
mon[i-1900][j]=q[j];
}
if(i%400==0||i%4==0&&i%100==0)
mon[i-1900][2]=29;
}
mon[2001-1900][12]=0;
mon[2001-1900][11]=3;
tmp=sg[2001-1900][11][4]=0;
_For(i,2001,1900){
_For(j,12,1){
_For(k,mon[i-1900][j],1){
if(j<12&&k<=mon[i-1900][j+1]){
// cout<<tmp<<endl;
For(l,0,2){
if(tmp!=l&&sg[i-1900][j+1][k]!=l){
sg[i-1900][j][k]=l;
break;
}
}
}
else if(j==12){
For(l,0,2){
if(tmp!=l&&sg[i-1900+1][1][k]!=l){
sg[i-1900][j][k]=l;
break;
}
}
}
else{
if(tmp==0)
sg[i-1900][j][k]=1;
else
sg[i-1900][j][k]=0;
}
tmp=sg[i-1900][j][k];
}
}
}
}
int main(){
init();
cin>>t;
int y,m,d;
while(t--){
cin>>y>>m>>d;
if(sg[y-1900][m][d]==0){
cout<<"NO\n";
}
else
cout<<"YES\n";
}
return 0;
}大意是两名玩家对于两个数字进行变换操作,每次操作只能将较大的数字减去较小数字的正整数倍且结果为非负数,当某个玩家可以使较小的数字达到0时游戏停止,该玩家获胜,问两名玩家皆采取最优策略,最终谁会获胜。
假设maxx是较大的数字,minn是较小的数字,可以想到:
minn=0时是先手必败态;
maxx%minn==0时是先手必胜态;
maxx>2*minn时是先手必胜态:若(maxx%minn,minn)是先手必败态,显然(maxx,minn)可以通过一次操作达到(maxx%minn,minn),所以是先手必胜态,若(maxx%minn,minn)是先手必胜态,则(maxx,minn)可以通过一次操作达到(maxx%minn+minn,minn),显然(maxx%minn+minn,minn)只能达到(maxx%minn,minn),所以(maxx%minn+minn,minn)是先手必败态,所以(maxx,minn)是先手必胜态;
maxx<2*minn时,则只能往下计算直到出现上述三种情况才能确定是必胜还是必败。
#include<iostream>
using namespace std;
int n,m;
bool dfs(int maxx,int minn){
if(minn==0){
return false;
}
if(maxx%minn==0||maxx>=2*minn){
return true;
}
return !dfs(minn,maxx-minn);
}
int main(){
while(cin>>n>>m){
if(n==0&&m==0)
break;
if(dfs(max(n,m),min(n,m))){
cout<<"Stan wins\n";
}
else
cout<<"Ollie wins\n";
}
return 0;
}C - Play a game
大意是两名玩家在一个n*n的棋盘上移动棋子,棋子的起始位置是角落,每次移动只能到相邻的没有经过的格子,问谁能获胜。
很容易就能看出规律,显然n为奇数时先手必败,偶数时必胜,链接是kuangbin大神的博客,思路比较清晰。
#include<iostream>
using namespace std;
int main(){
int n;
while(cin>>n,n){
if(n%2)
cout<<"ailyanlu\n";
else
cout<<8600<<endl;
}
return 0;
}大意是一堆石子有n个,每次操作可以取走其中不超过m个石子,两人轮流进行操作,最先取光的人获胜,给定n,m问是先手胜还是后手胜。
大致的做法是求出sg函数,事实上sg函数关于m的规律还是挺好找的,sg(n)==0当且仅当n%(m+1)==0。
#include<iostream>
using namespace std;
int t,m;
int main(){
int n;
cin>>t;
while(t--){
cin>>n>>m;
if(n%(m+1)!=0){
cout<<"first\n";
}
else
cout<<"second\n";
}
return 0;
}E - Good Luck in CET-4 Everybody!
题目大意是给定n张牌,两个玩家轮流抓牌,每个人只能抓2的幂次张牌,先抓完牌的获胜。
n的范围不大,操作数也不多,打表求sg函数即可。
#include<iostream>
using namespace std;
int n,sg[1005],f[11];
bool flag[20];
void init(){
sg[0]=0;
f[0]=1;
for(int i=1;i<=10;i++)
f[i]=f[i-1]*2;
for(int i=1;i<=1000;i++){
for(int j=0;f[j]<=i;j++){
flag[sg[i-f[j]]]=true;
}
for(int j=0;j<20;j++){
if(!flag[j]){
sg[i]=j;
break;
}
}
for(int j=0;j<20;j++)
flag[j]=false;
}
}
int main(){
init();
while(cin>>n){
if(sg[n]==0){
cout<<"Cici\n";
}
else
cout<<"Kiki\n";
}
return 0;
}1堆石子有n个,两人轮流取.先取者第1次可以取任意多个,但不能全部取完.以后每次取的石子数不能超过上次取子数的2倍。取完者胜.先取者负输出"Second win".先取者胜输出"First win".
可以找规律,但是本人最开始暴力打前几个数的sg函数表打错了,导致wa了好几发,最后手算十几项猜是满足斐波那契数列的才是必败态,AC了。
模型介绍见世界冠军的博客:点击打开链接
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=a;i<=b;i++)
#define INF 0x3f3f3f3f
#define N 1005
#define db double;
int n,m,t,ans;
template<class T>
inline bool scan_d(T &ret){
char c;
int sgn;
if(c==getchar(),c==EOF) return 0;
while(c!='-'&&(c<'0'||c>'9')) c=getchar();
sgn=(c=='-')?-1:1;
ret=(c=='-')?0:(c-'0');
while(c==getchar(),c>='0'&&c<='9') ret=ret*10+c-'0';
ret*=sgn;
return 1;
}
map<ll,bool> mp;
void init(){
ll f[60];
f[0]=2,f[1]=3;
for(int i=2;i<60;i++){
f[i]=f[i-1]+f[i-2];
}
for(int i=0;i<60;i++){
mp[f[i]]=true;
}
}
int main(){
init();
while(~scanf("%d",&n),n){
if(mp.find(n)!=mp.end()){
cout<<"Second win\n";
}
else{
cout<<"First win\n";
}
}
return 0;
}G - 邂逅明下
大意是给定n,p,q分别代表硬币个数及每次操作至少取p枚硬币,至多取q枚硬币,当硬币数不足p时必须取完,最后一次取硬币的人算输,问先手是否有必胜策略。
很容易得出:
n<=p时,先手必败;
p<n<=q+p时,先手总能通过一次操作使得n'<=p,因此先手必胜;
p+q<n<=2*p+q时,先手无论如何操作,n'必然落在(p,q+p]区间,所以先手必败;
2*p+q<n<=2*(p+q)...
可见先手必胜与必败是交替出现的,且规律为(n-1)%(q+p)<p时,先手必败,否则先手必胜。
#include<cstdio>
#include<iostream>
using namespace std;
int n,p,q;
int main(){
while(~scanf("%d %d %d",&n,&p,&q)){
if((n-1)%(p+q)<p){
cout<<"LOST\n";
}
else
cout<<"WIN\n";
}
return 0;
}大意是对于n堆石子,两名玩家轮流取石子,可以取某一堆任意数量的石子,也可以把某一堆石子分成两堆石子,取走最后的石子的玩家获胜,问谁能获胜。
起初将smaller看成simillar,就想错了,因为平分后的状态相当于取完了这堆石子,就和原始的组合Nim博弈一样了,然后wa了...最后看对题意后找规律发现,sg(4*k-1)=4*k,sg(4*k)=4*k-1,其余情况sg(x)=x,因此只需判断下石子的数量si是否为前面那两种特殊情况,对所有堆的石子数的sg函数取异或即可。
#include<iostream>
#include<cstdio>
using namespace std;
#define ll long long
int t,n,a[1000005];//第一次看错题以为分成simillar,原来是smaller。
int main(){
cin>>t;
while(t--){
cin>>n;
long long ans=0;
for(int i=0;i<n;i++){
scanf("%d",&a[i]);
if(a[i]%4==3)
a[i]++;
else if(a[i]%4==0)
a[i]--;
ans^=a[i];
}
if(ans==0){
cout<<"Bob\n";
}
else
cout<<"Alice\n";
}
return 0;
}还是两个人玩游戏,一堆箱子编号从1到n,每次操作只能选取满足编号B<A&&(A+B)%3==0&&(A+B)%2==1且A非空的两个箱子,然后从A中往B中转移任意数量的卡片,无法操作的人输掉游戏。
这题说实话我没想到什么方法...最终没忍住看了kuangbin大神的博客,居然联想到二分图orz。
大概就是可以把箱子分为左边集合和右边集合。(下面一段话转自kuangbin大神博客,这是链接)
1.如果可以从A拿卡片到B,连一条从A到B的边。把所有box编号x满足((x%3==0&&x%2==1) || x%3==1)这个条件的放左边,其他放右边,不难发现
a) 只有从左边到右边的边或从右到左的边。
b) 所有不能拿卡片出去的box都在左边。
2. 证明左边的box并不影响结果。假设当前从右边的局势来看属于输家的人为了
摆脱这种局面,从左边的某盒子A拿了n张卡片到B,因为B肯定有出去的边,对手
会从B再取走那n张卡片到左边,局面没有变化
3. 于是这就相当于所有右边的box在nim游戏。
#include<iostream>
#include<cstdio>
using namespace std;
int t,n,a;
int main(){
cin>>t;
int cas=0;
while(t--){
cin>>n;
int ans=0;
for(int i=1;i<=n;i++){
scanf("%d",&a);
if(i%3==1||(i%3==0&&i%2==1))
continue;
ans^=a;
}
cout<<"Case "<<(++cas)<<": ";
if(ans==0)
cout<<"Bob\n";
else
cout<<"Alice\n";
}
return 0;
}J - Daizhenyang's Coin
大意是一堆硬币,一部分朝上,一部分朝下,每次操作可以翻转1、2或3枚硬币且必须保证每次翻转的硬币中最右边的那枚是朝上的,现给出n以及n个位置,代表朝上的硬币的位置,需要注意同一个位置可能出现两次,如果对于给定的局面先手必胜则输出No,否则输出Yes。
首先要知道,翻硬币游戏整个局面的SG值,就是该局面中所有朝上位置的SG值的异或。
因此可以先找规律求每个位置朝上时的SG值,可以得到:
位置:0 1 2 3 4 5 6 7 8...
SG值:1 2 4 7 8 11 13 14 16...
可以发现对于位置x,SG值要么是2x,要么是2x+1。更神奇的是,所有SG值的二进制形式1的个数都是奇数!
因此,我们先去重,然后对于朝上的每个位置求出SG值并异或即可。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=a;i<=b;i++)
#define INF 0x3f3f3f3f
#define N 1005
#define db double;
int n,m;
map<int,bool> mp;
int sg(int x){
int res=2*x,s=0;
while(res){
if(res&1) s++;
res>>=1;
}
return (s%2==1?2*x:2*x+1);
}
int main(){
while(cin>>n){
int ans=0;
For(i,1,n){
cin>>m;
mp[m]=true;
}
if(((int)mp.size())%2==1){
//这里用到一个结论,所有位置SG值异或后为0的充要条件是偶数个数且位置异或为0
cout<<"No\n";
mp.clear();//这里忘记清理mapWA了好多发
continue;
}
map<int,bool>::iterator it=mp.begin();
for(;it!=mp.end();it++){
//ans^=sg(it->first);//当然也可以不用结论,而是直接通过判断所有SG值异或后是否为0
ans^=it->first;
}
if(ans==0){
cout<<"Yes\n";
}
else
cout<<"No\n";
mp.clear();
}
return 0;
}K - Alice's Game
大意是给n个长宽分别为xi*yi的矩形,Alice(先手)每次只能对其中一个xi>=2的矩形横着切,即把xi*yi变为a*yi和b*yi两个矩形(a+b=xi),Bob每次只能对其中一个yi>=2的矩形竖着切,即把xi*yi变为 xi*a和xi*b两个矩形(a+b=yi),先不能再切的人失败,问谁胜谁负。
因为我是按专题的过题人数由多至少顺序写的题,因此这题可以说是我目前碰到的最难的一道题了。因为是多个矩形,由此前累积的经验我很自然的想到sg函数异或....这题似乎行不通?
卡了两天,依然没找到SG函数的规律,无奈只好网上找题解了,看到一个说是贪心,然后又思考了很久,只有一点大致的思路,可能不是很详尽, 主要靠规律。。。
我们假设有这么一个值g(x,y)代表Alice比Bob可以多动几刀,若为负则说明Bob可动刀数多。
首先很容易考虑到对于(n,1)的矩形,不论先后都是Alice可以切n/2-1刀而Bob切不了,而对于(1,m)的矩形,不论先后都是Alice切不了而Bob可以切m/2-1刀,即g(x,1)=x/2-1,g(1,y)=-(y/2-1);
然后发现还有一部分特殊的矩形,谁先切谁输,比如(1,1),(2,2),(3,3)...我们多试几个,大概可以发现,这种矩形是以2的整数幂为界限,即对于所有同属于某一[2^k,2^(k+1)-1]区间内的数两两组合(允许相同)形成的所有矩形都是这种特殊的矩形。而这种矩形都是先切者必输的,因此显然,把所有的这种矩形放到一边不考虑不会影响胜负(对于游戏过程中某次操作切出来的这种矩形一样也不考虑)。
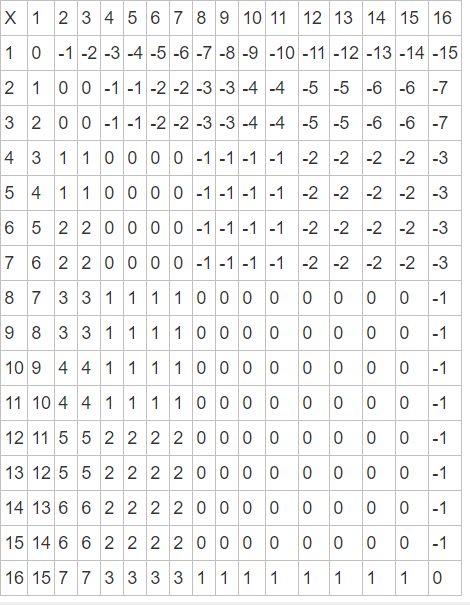
最后也是最核心的,我们该如何推出除了上述两种矩形之外其他矩形的g值。对于(x,y),假设Alice先切这个矩形,将之分为(x',y)和(x'',y)且两个矩形都不是特殊的矩形,那么g(x,y)=g(x',y)+g(x'',y)+1。假设Bob先切,将之分为(x,y')和(x,y'')且均不是特殊矩形,那么g(x,y)=g(x,y')+g(x,y'')-1,同样平分y时最优。那么先手怎么切g(x,y)值对他来说会最优呢?由上面两个式子找规律令g(x,y)最符合要求即可。
下面是(x,y)矩形对应的g(x,y),为了方便处理,我们令特殊矩形的g值为0,因为不影响结果。
从上图可以看出规律,对于任意(x,y)(x>=2,y>=2)都有g(x,y)==g(x/2,y/2),因此我们可以递归直到x==1或y==1时即可求出结果。
#include<iostream>
using namespace std;
#define ll long long
int t,n,xi,yi;
int solve(int x,int y){
if(x==1)
return 1-y;
if(y==1)
return x-1;
return solve(x/2,y/2);
}
int main(){
cin>>t;
int cas=0;
while(t--){
cin>>n;
ll ans=0;
for(int i=0;i<n;i++){
cin>>xi>>yi;
if(xi!=yi)
ans+=solve(xi,yi);
}
cout<<"Case "<<(++cas)<<": ";
if(ans<=0){
cout<<"Bob";
}
else
cout<<"Alice";
cout<<"\n";
}
return 0;
}L - No Gambling
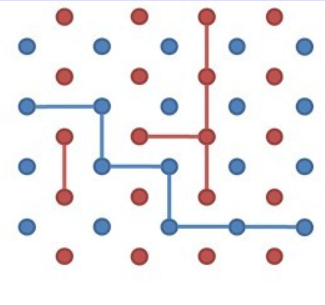
大意是给出一个数字n,然后两名玩家在一个图上(如下图,n=4)进行连线操作,先手连蓝色的,后手连红色的,要求每个点只能连相邻(上下左右)的同种颜色的点且两种颜色的线不能交叉,先手需要从蓝点的最左边一直 连到最右边,后手需要从红点的最上边一直连到最下边,问先手和后手谁胜。(第二张图是一种可能的连法,先手胜)

可以先小数据手画猜规律,我只画了2、3、4就猜出了规律。。。不论n为多少,先手必胜!然后就AC了。。。大致理性分析一 下,就是因为图是对称的,先手有优势...本来想去找大神们的博客看看严密的推理过程,暂时没有找到= =。
#include<bits/stdc++.h>
using namespace std;
int n;
int main(){
while(cin>>n,n!=-1){
cout<<"I bet on Oregon Maple~\n";
}
return 0;
}大意是n个硬币排成一圈,每次只能取1-k个连续位置的硬币,取完的那个人获胜,问先手和后手谁胜。
写这题的时候突然想到V8学长暑期集训时和某个同学玩的一个游戏,算是这题的简化版——硬币不是排成一圈,而是排成一列。先说说简化版吧,可以想到:
若n'<=k,那么势必第一次就可以被先手取完,先手必胜;
否则,当n'为奇数时,先手取中间那一个,然后剩下的局面就是左右对称的,先手只需与后手对称取即可赢,先手必胜;当n'为偶数时,先手取中间对称的偶数个,依然使得两边对称,先手必胜(若此时先手无法做到取偶数个,即k=1,则先手必败)。
那么现在来考虑这道题,事实上无论先手如何取,第一次取硬币后就转化成了简化版!
假设先手第一次取了x个(1<=x<=k),那么就转化为简化版的n'=n-x的局面,只不过后手成了简化版先手,很容易就能求出结果。
#include<bits/stdc++.h>
using namespace std;
int n,m,t;
int main(){
cin>>t;
int cas=0;
while(t--){
cin>>n>>m;
cout<<"Case "<<(++cas)<<": ";
if(m==1){
if(n&1) cout<<"first";
else cout<<"second";
}
else{
if(n<=m){
cout<<"first";
}
else
cout<<"second";
}
cout<<"\n";
}
return 0;
}
大意是两个人进行捐款,规则是:
1、最初的捐款箱是空的;
2、两人轮流捐款,每次捐款额必须为正整数,并且每人每次捐款最多不超过m元(1<=m<=10)。
3、最先使得总捐款额达到或者超过n元(0<n<10000)的一方为胜者,则其可以亲赴灾区服务。
先手必胜输出Grass,否则输出Rabbit。
我们可以分析一下,若n<=m,先手必胜,若n==m+1,无论先手怎么捐款下一次都会落到n<=m,因此先手必败,若m+1<n<=2*m+1,先手可以使下一次变成n==m+1,因此先手必胜......可以发现只有当n%(m+1)==0时先手必败。
其实这就是有n个石子,每次可以取不超过m个的Nim游戏,和前面的D题一毛一样。。。。
#include<iostream>
using namespace std;
int n,m;
int main(){
int t;
cin>>t;
while(t--){
scanf("%d %d",&n,&m);
if(n%(m+1)==0){
cout<<"Rabbit\n";
}
else
cout<<"Grass\n";
}
return 0;
}O - Public Sale
可以理解为求N题的先手必胜的第一次的合理的取法。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=a;i<=b;i++)
#define INF 0x3f3f3f3f
#define N 1005
#define db double;
int n,m,t,ans;
int main(){
while(cin>>n>>m){
if(n%(m+1)==0){
cout<<"none";
}
else{
if(n<=m){
For(i,n,m){
cout<<i;
if(i!=m)
cout<<" ";
}
}
else{
cout<<n%(m+1);
}
}
cout<<"\n";
}
return 0;
}P - Being a Good Boy in Spring Festival
这题算是Q题的简化版,堆数范围小一点,把输出可能的取法改为可能的取法的数目即可。
#include<iostream>
#include<cstdio>
using namespace std;
int m,a[105];
int main(){
while(cin>>m,m){
int ans=0,aans=0;
for(int i=0;i<m;i++){
scanf("%d",&a[i]);
ans^=a[i];
}
if(ans==0){
cout<<ans;
}
else{
int k=ans,s=0;
while(k){
s++;
k>>=1;
}
int tmp,num;
for(int i=0;i<m;i++){
tmp=a[i];
num=0;
while(tmp){
num++;
tmp>>=1;
}
if(num>=s&&a[i]>(a[i]^ans)){
aans++;
}
}
cout<<aans;
}
cout<<"\n";
}
return 0;
}m堆石子,两人轮流取。只能在1堆中取.取完者胜.先取者负输出No。先取者胜输出Yes,然后输出怎样取子。例如5堆 5,7,8,9,10先取者胜,先取者第1次取时可以从有8个的那一堆取走7个剩下1个,也可以从有9个的中那一堆取走9个剩下0个,也可以从有10个的中那一堆取走7个剩下3个。
m堆石子的Nim游戏,不过我们还需要知道如果当前是先手必胜态的话,通过如何操作可以变为一个先手必败态。
假设某个局面为先手必胜态,且a1^a2^...^am=k(k不为0),对于所有二进制位数大于等于k的二进制位数的ai(易知至少有一个这样的i),如果ai^k<ai,则说明有一种合法的移动可以使得ai变为ai^k,输出所有可能的方案即可,
#include<iostream>
#include<cstdio>
using namespace std;
int m,a[200005];
int main(){
while(cin>>m,m){
int ans=0;
for(int i=0;i<m;i++){
scanf("%d",&a[i]);
ans^=a[i];
}
if(ans==0){
cout<<"No\n";
}
else{
cout<<"Yes\n";
int k=ans,s=0;
while(k){
s++;
k>>=1;
}
int tmp,num;
for(int i=0;i<m;i++){
tmp=a[i];
num=0;
while(tmp){
num++;
tmp>>=1;
}
if(num>=s&&a[i]>(a[i]^ans)){//起初我并没有加上a[i]>(a[i]^ans),但还是AC了,写这博客分析的时候觉得不对,m=2,两堆分别为4 7就把自己叉掉了
cout<<a[i]<<" "<<(a[i]^ans)<<"\n";
}
}
}
}
return 0;
}有两堆石子,数量任意,可以不同。游戏开始由两个人轮流取石子。游戏规定,每次有两种不同的取法,一是可以在任意的一堆中取走任意多的石子;二是可以在两堆中同时取走相同数量的石子。最后把石子全部取完者为胜者。现在给出初始的两堆石子的数目,如果轮到你先取,假设双方都采取最好的策略,问最后你是胜者还是败者。
这是威佐夫博奕的模板题,自己推了挺久才推出了一个大概的规律——假设两堆石子数分别为a和b,对于a和b的每一个差值都有且只有一组特定的值可以使得先手必败,且除了(0,0)外,每个自然数都只出现在其中一组中——但是想不到如何实现。。。
搜了题解后发现居然和黄金分割比有关系...假设a小于等于b,k=b-a,当且仅当a==(int)((sqrt(5)+1)/2.0*k)时为先手必败态。
#include<iostream>
#include<cmath>
using namespace std;
int n,m;
double p=(sqrt(5)+1)/2.0;
int main(){
while(cin>>n>>m){
int a=min(n,m),b=max(n,m),k=b-a;
if(a==(int)(p*k)){
cout<<"0\n";
}
else
cout<<1<<"\n";
}
return 0;
}某些博客上讲的方法是,因为a=(int)((sqrt(5)+1)/2.0*k),所以可通过k=(int)(a*(sqrt(5)-1)/2.0),然后当b==a+k||b==a+k+1时即为先手必败态。我最开始是按这个写的,AC了,但是事实上,究竟是b==a+k还是b==a+k+1我并没有判断,那么势必会导致一部分本来不是先手必败态的被误判成了先手必败态!(比如4 6就能叉掉我下面的AC代码,4 6时应该是先手必胜,4 7才是先手必败。。。)
#include<iostream>
#include<cmath>
using namespace std;
int n,m;
int main(){
while(cin>>n>>m){
int a=min(n,m),b=max(n,m),k=a*(sqrt(5)-1)/2;
if(b==a+k||b==a+k+1){
cout<<"0\n";
}
else
cout<<1<<"\n";
}
return 0;
}实际上第二种方法应该是这样的:
因为a=(int)((sqrt(5)+1)/2.0*k),所以可先计算k=(int)(a*(sqrt(5)-1)/2.0),若a、b为先手必败态,则a只可能为a[k]或a[k+1]。判断a==(int)((sqrt(5)+1)/2.0*k)是否成立,是的话,a=a[k],判断b==a[k]+k是否成立,是的话先手必败态,否则先手必胜态;否则a=a[k+1],判断b==a[k+1]+k+1是否成立,是的话先手必败态,否则先手必胜态。
把我上面的代码稍微修改就是正解了。。。
#include<iostream>
#include<cmath>
using namespace std;
int n,m;
int main(){
while(cin>>n>>m){
int a=min(n,m),b=max(n,m),k=a*(sqrt(5)-1)/2;
if(a==(int)(k*(sqrt(5)+1)/2.0)&&b==a+k||a==(int)((k+1)*(sqrt(5)+1)/2.0)&&b==a+k+1){
cout<<"0\n";
}
else
cout<<1<<"\n";
}
return 0;
}有两堆石子,数量任意,可以不同。游戏开始由两个人轮流取石子。游戏规定,每次有两种不同的取法,一是可以在任意的一堆中取走任意多的石子;二是可以在两堆中同时取走相同数量的石子。最后把石子全部取完者为胜者。现在给出初始的两堆石子的数目,如果轮到你先取,假设双方都采取最好的策略,问最后你是胜者还是败者。如果你胜,你第1次怎样取子?
类似于取m堆石子游戏,那题是Nim游戏先手必胜态到先手必败态可能的取法,这题就是需要威佐夫博奕的先手必胜态到先手必败态可能的取法。
假设原来的先手必胜局面两堆石子分别为a,b(a<=b),那么到达先手必败态(a',b')的可能操作有:
1. a、b取相同个数石子后到达。即到达后a、b差值不变,因此我们可以通过已知的k算出这种情况下a'、b'分别是多少,然后判断a、b是否大于等于a'、b',是的话这就是一种合理的取法。
2. a不变,只对b取子,这里有两种可能,取完后达到的先手必败态a'==a或者b'==a,假设是前者,可以通过前一题的第二种方法算出k值,求出b'的值,然后判断是否能达到该状态,能的话是一种合理的取法;如果是后者,同样可以通过前一题的第二种方法求出a',然后判断该状态是否可达。(由威佐夫博弈先手必败态组合的规律,显然对于一个确定的a(a>=0),该数值要么是某个状态的a',要么是某个状态的b',不可能都是!)
3. b不变,只对a取子,因为a<=b,所以取子后a只可能为a',b=b'。通过前一题第二种方法计算出a',看该状态是否可达。
不过写这题的时候有点冒傻气,写得又长又丑。。。(居然用二分法来找k我也是个人才,虽然这一过程也不过是log级别的。。。还有用map来判哪种取法先输出,其实我先判第一种情况,可以的话先输出就完了。。。)
#include<iostream>
#include<cmath>
#include<map>
using namespace std;
int a,b;
double p=(sqrt(5)+1)/2.0;
struct node{
int x,y,r;
friend bool operator<(node a,node b){
return a.r<b.r;
}
}qaq;
map<node,bool> m;
int main(){
while(cin>>a>>b,a||b){
int k=b-a,r=0;
int a1=(int)(p*k);
if(a==a1){
cout<<"0\n";
}
else{
cout<<1<<"\n";
if(a>a1){//差值不变
qaq.x=a1,qaq.y=a1+k,qaq.r=r++;
m[qaq]=true;
}
int k1=a*(sqrt(5)-1)/2.0,k2=k1+1,a2=p*k1,a3=k2*p,b1=a+k1,b2=a+k2,a4;
//a不变,可能做a,也可能做b
int l=0,r=1000000000,mid,nowk=-1,tmp;
while(l<=r){
mid=(l+r)>>1;
tmp=(int)(p*mid)+mid;
if(a>tmp){
l=mid+1;
}
else if(a==tmp){
nowk=mid;
break;
}
else{
r=mid-1;
}
}
if(nowk!=-1){
a4=a-nowk;
qaq.x=a4,qaq.y=a,qaq.r=r++;
m[qaq]=true;
}
if(b>b2){
if(a==a3){
qaq.x=a,qaq.y=b2,qaq.r=r++;
m[qaq]=true;
}
else if(a==a2){
qaq.x=a,qaq.y=b1,qaq.r=r++;
m[qaq]=true;
}
}
else if(b==b2){
if(a==a1){
qaq.x=a,qaq.y=b2,qaq.r=r++;
m[qaq]=true;
}
}
l=0,r=1000000000,nowk=-1;
while(l<=r){
mid=(l+r)>>1;
tmp=(int)(p*mid)+mid;
if(b>tmp){
l=mid+1;
}
else if(b==tmp){
nowk=mid;
break;
}
else{
r=mid-1;
}
}
if(nowk!=-1){
a4=b-nowk;
if(a>a4){
qaq.x=a4,qaq.y=b,qaq.r=r++;
m[qaq]=true;
}
}
}
map<node,bool>::iterator it=m.begin();
for(;it!=m.end();it++){
cout<<(it->first.x)<<" "<<(it->first.y)<<"\n";
}
m.clear();
}
return 0;
}T - A Multiplication Game
大意是初始p为1,每次可以对其进行乘以2到9的操作,先达到p>=n的获胜,问对于给定的n采用最优策略先手和后手谁胜。
分析一下:
对于2<=n<=9,显然先手必胜;对于10<=n<=18,同样显然先手必败;而对于19<=n<=162,先手必胜...
我们可以反着来思考,把原题当作是对n进行除以2到9且向上取整的操作。
然后考虑取法的边界2和9,显然先手必胜和必败的临界值是由它们决定的(这个地方和2018西安邀请赛的D有点像,可惜当时完全不会博弈...),假设某个区间[l,r]的值全是先手必败态,那么区间[2*l-1,9*r]的值就是先手必胜态,因为都可以通过一次操作落入[l,r]区间。
#include<iostream>
using namespace std;
#define ll long long
ll n;
ll f[40];
void init(){
f[0]=9;
for(int i=1;i<40;i++){
if(i%2==1)
f[i]=f[i-1]*2;
else
f[i]=f[i-1]*9;
}
}
int main(){
init();
int pos;
while(cin>>n){
for(int i=0;i<40;i++){
if(n<=f[i]){
pos=i;
break;
}
}
if(pos%2==0){
cout<<"Stan";
}
else
cout<<"Ollie";
cout<<" wins.\n";
}
return 0;
}剩下的再慢慢补。。。。。。