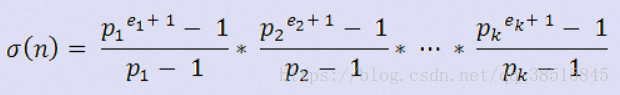这道题我很久以前写过一篇博客,这里就不再讨论,做法就是欧拉函数打表然后二分查找(据说暴力查找也行?)即可。
B - Prime Independence
这题表示目前还不会,看题解似乎与二分图有关。。。知识盲区,估计挺久以后才有时间补
C - Aladdin and the Flying Carpet
题意大致是对给定的a、b,求满足x*y==a&&x>=b&&y>=b&&x<y的(x,y)的个数。
我的解法是先线性筛打1e6的素数表,当b>sqrt(a)||b*b==a时显然没有满足条件的(x,y),ans=0;而当b<=sqrt(a)时,利用素数表把a分解质因数,再对质因数暴搜寻找符合条件的值,每找到一 个满足x>=sqrt(b)&&x*x!=a&&x<=sqrt(a)的x就ans++,因为x*y==a,所以y一定大于sqrt(a),也就大于b。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define N 1000002
int t,ans;
ll a,b;
bool notprime[N];
int prime[100005],cnt;
void init(){
notprime[1]=true;
for(int i=2;i<N;i++){
if(!notprime[i])
prime[cnt++]=i;
for(int j=0;j<cnt&&i*prime[j]<N;j++){
notprime[i*prime[j]]=true;
if(i%prime[j]==0)
break;
}
}
}
int pcnt,e[105];
ll p[105];
void fenjie(ll x){//把x分解为p[0]^e[0] * p[1]^e[1] * ... * p[pcnt-1]^e[pcnt-1]
pcnt=0;
memset(e,0,sizeof(e));
for(int i=0;i<cnt&&prime[i]<=x;i++){
if(x%prime[i]==0){
p[pcnt]=prime[i];
while(x%prime[i]==0)
x/=prime[i],e[pcnt]++;
pcnt++;
}
}
if(x>1){
p[pcnt]=x,e[pcnt++]++;
}
}
void dfs(int now,ll s){//通过分解的质因数枚举x的因子,不懂的可能需要了解一下算术基本定理
if(s>sqrt(a))//若当前枚举的因子s已经大于sqrt(a),显然之后所有情况也不符合条件,剪掉
return;
if(now==pcnt){//枚举完所有素因子的个数后,判断s是否符合条件
if(s>=b&&(s*s)!=a)
ans++;
return;
}
for(int i=0;i<=e[now];i++){//枚举因子s中素因子p[now]的个数
if(i==0)
s*=1;
else
s*=p[now];
dfs(now+1,s);
}
}
int main(){
init();
cin>>t;
int cas=0;
while(t--){
scanf("%lld %lld",&a,&b);
ans=0;
if(b<=(int)sqrt(a)){
fenjie(a);
dfs(0,1);
}
cout<<"Case "<<++cas<<": ";
cout<<ans<<"\n";
}
return 0;
}题意大致是定义了一个sigma(n)(如下图),对给定的n,需要求从i从1到n所有的sigma(i)中偶数的个数。
首先我们可以把这个式子化一下,变成sigma(n)=(p1-1)*(p1^e1+p1^(e1-1)+...+1)/(p1-1)*...*(pk-1)*(pk^ek+pk^(ek-1)+...+1)/(pk-1),约去分母,即为sigma(n)=(p1^e1+p1^(e1-1)+...+1)*...*(pk^ek+pk^(ek-1)+...+1)。
从这个式子可以发现,当n含有的除了2以外的素因子的幂次只要有一个为奇数时sigma(n)就为偶数。
为什么呢?首先,除了2以外的素因子都是奇数,奇数的任意次幂均为奇数,奇数的0次幂,假设奇数的k次幂到0次幂的和为奇数,则奇数的k+1次幂到0次幂的和为 (奇数)+(奇数的k+1次幂),显然是偶数,即奇数的奇数次幂到0次幂的和为偶数。而偶数乘以任何数都是偶数,因此满足上述条件的sigma(n)为偶数。
然后逆向思考一下,什么情况下sigma(n)不为偶数?自然就是除了2以外的素因子的幂次全部都是偶数的时候啦!这不就是平方数嘛!当然,我们还需要考虑一下素因子2,因为它是个偶数,所以导致除了考虑平方数以外还需要考虑它们的2倍(不需要考虑4倍是因为 (平方数)*4也是平方数,避免重复计数)!因此,对于给定的n,1到n中sigma(i)为偶数的个数有n-sqrt(n)-sqrt(n/2)。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=a;i<=b;i++)
#define INF 0x3f3f3f3f
#define N 1005
#define db double;
int t;
ll n,ans;
int main(){
cin>>t;
int cas=0;
while(t--){
cin>>n;
ans=0;
ans+=(ll)sqrt(n),ans+=(ll)sqrt(n/2),ans=n-ans;
cout<<"Case "<<(++cas)<<": "<<ans<<endl;
}
return 0;
}题目大意是对于给定的n和k,求出n^k的最高的三位数字和最低的三位数字。这题似乎和我写过的xdoj1029 数一的逆袭有点像。
首先,求低三位很简单嘛,就是((n%1000)^k)%1000,直接上快速幂。
那么,求高三位该怎么办呢?高精度暴力乘法?肯定超时。这时候我们想到了利用浮点数。假设x=n^k,y=log10(n^k)=klog10(n),令y1=(int)y,y2=y-y1,可知x=10^(y1+y2)=(10^y1)*(10^y2),10^y1只有x的最高位是1,其他位全是0,即每一位的数值是什么由10^y2确定,且10^y2的值为1.多,因此我们只需要求出(int)((10^y2)*100)即为高三位的值。
#include<iostream>
#include<cmath>
#include<string>
#include<algorithm>
using namespace std;
int t,n,k;
string aans;
#define db double
void qpow(int x,int y,int p){
aans.clear();
int ans=1;
while(y){
if(y&1) ans=ans*x%p;
y>>=1;
x=x*x%p;
}
int tt=ans;
while(ans){
aans+=(ans%10+'0');
ans/=10;
}
if(tt==0)//需要注意的是末三位的输出格式,需用前导0补齐三位,这里我写的比较麻烦且无脑
aans+="0";
if(tt<10){
aans+="00";
}
else if(tt<100){
aans+="0";
}
reverse(aans.begin(),aans.end());
}
int main(){
cin>>t;
for(int cas=1;cas<=t;cas++){
cin>>n>>k;
cout<<"Case "<<cas<<": ";
db ans=k*log10(n);
qpow(n%1000,k,1000);
cout<<(int)(pow(10,ans-(int)ans)*100)<<" "<<aans<<endl;
}
return 0;
}题目与哥德巴赫猜想有关,还记得之前宁夏邀请赛网赛的时候写一道哥德巴赫猜想的题因为溢出T成了傻逼。
题意:对给定的n,求满足a<=b&&a+b==n的素数(a,b)的对数。
受网赛那题的影响,还有空间大小计算失误,以为1e7素数表打不了,开始居然写了个miller_rabbin素数测试,成功的T了。。。然后再次计算了空间大小,转为素数筛,对每个n枚举素数a,通过bool数组O(1)判b即可。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=a;i<=b;i++)
#define INF 0x3f3f3f3f
#define N 10000004
#define db double;
int n,t,cnt,prime[800005],y,ans;//这里一个小技巧,先本地数组开大一点,打完表看究竟有多少个,再将数组尽量开小,直接1e7会爆空间
bool notprime[N+1];
void init(){
notprime[1]=true;
For(i,2,N){
if(!notprime[i]) prime[cnt++]=i;
for(int j=0;j<cnt&&prime[j]*i<=N;j++){
notprime[prime[j]*i]=true;
if(i%prime[j]==0){
break;
}
}
}
}
int main(){
init();
int cas=0;
cin>>t;
while(t--){
ans=0;
cin>>n;
for(int j=0;prime[j]<=n/2;j++){
y=n-prime[j];
if(notprime[y]==0) ans++;
}
cout<<"Case "<<(++cas)<<": "<<ans<<"\n";
}
return 0;
}大意:定义H(n)=sigma(n/i)(i从1到n),对给定的n求H(n)。
我们可以把i以sqrt(n)为分界进行考虑,对于小于等于sqrt(n)的i,n/i的值各不相同,需要一个个枚举i来得到n/i的值;
对于大于等于sqrt(n)的i,n/i的个数为n/(n/i)-n/(n/i+1),因为很多都是相同的,所以没必要一个个枚举i,可以通过枚举n/i的值解决,因为i大于等于sqrt(n),所以n/i小于等于sqrt(n)。注意当n/i==i时会重复计数,需要特判。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=a;i<=b;i++)
#define INF 0x3f3f3f3f
#define N 50005
#define db double;
int n,t,p[N],cnt,y;
ll ans=0;
template<class T>
inline bool scan_d(T &ret){
char c;
int sgn;
if(c=getchar(),c==EOF) return 0;
while(c!='-'&&(c<'0'||c>'9')) c=getchar();
sgn=(c=='-')?-1:1;
ret=(c=='-')?0:(c-'0');
while(c=getchar(),c>='0'&&c<='9') ret=ret*10+c-'0';
ret*=sgn;
return 1;
}
int main(){
scan_d(t);
For(cas,1,t){
scan_d(n);
int sn=sqrt(n);
ans=0;
for(int i=1;i<=sn;i++){
ans+=(n/i-n/(i+1))*1ll*i+n/i;
if(n/i==i)
ans-=i;
}
printf("Case %d: %lld\n",cas,ans);
}
return 0;
}H - Pairs Forming LCM
题意:对于给定的n,求有多少对(i,j)(i从1到n,j从1到n,i<=j),满足i和j的最小公倍数为n。
这题主要用到算术基本定理。将n分解质因数,可知,i和j的最小公倍数为n,则i和j只能含有n所含有的质因子,且i和j中至少有一个数该质因子的幂次为n中该质因子的幂次。
假设n分解为p1^e1 * p2^e2 * ... * pk^ek,先抛开i<=j这个条件,总情况数为(2*e1+1)*(2*e2+1)*...*(2*ek+1)——对于每个质因子, 先选定i或j其中一个为e次幂,另一个则可以从0到e次幂,因此为2*(e+1),又因为两个都是e的情况计算了两次,所以减1,再把所有素因子的情况乘起来。
再考虑i<=j,因为i<j和i>j是完全对称的,i==j只有i=j=n一种情况,那么只需要去掉对称的一半情况数即可。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=a;i<=b;i++)
#define INF 0x3f3f3f3f
#define N 10000005
#define db double
int t;
ll n,ans;
template<class T>
inline bool scan_d(T &ret){
char c;
int sgn;
if(c=getchar(),c==EOF) return 0;
while(c!='-'&&(c<'0'||c>'9')) c=getchar();
sgn=(c=='-')?-1:1;
ret=(c=='-')?0:(c-'0');
while(c=getchar(),c>='0'&&c<='9') ret=ret*10+c-'0';
ret*=sgn;
return 1;
}
bool notprime[N];
int cnt,prime[1000005];
void init(){
notprime[1]=true;
For(i,2,10000001){
if(!notprime[i]) prime[cnt++]=i;
for(int j=0;j<cnt&&prime[j]*i<=10000001;j++){
notprime[prime[j]*i]=true;
if(i%prime[j]==0)
break;
}
}
}
int p[205],e[205],pcnt;
void fenjie(ll x){
pcnt=0,ans=1;
memset(e,0,sizeof(e));
for(int i=0;i<cnt&&prime[i]<=x;i++){
if(x%prime[i]==0){
p[pcnt]=prime[i];
while(x%prime[i]==0){
e[pcnt]++;
x/=prime[i];
}
ans*=(2*e[pcnt++]+1);
}
}
if(x>1){
p[pcnt]=x,e[pcnt]++;
ans*=(2*e[pcnt++]+1);
}
cout<<(ans-1)/2+1<<"\n";
}
int main(){
init();
scan_d(t);
For(cas,1,t){
scan_d(n);
cout<<"Case "<<cas<<": ";
fenjie(n);
}
return 0;
}题意:对给定n求Hn。
这题想了挺久的,总感觉除了暴力没啥好方法,但是数组又开不下。。。这可咋整。
还好灵光一闪,想到了分区间打表(以前从来没见过这玩意, 所以自己琢磨了很久才想到)。方法就是将很大的数据量分为多个区间,比如本题至多1e8,可分为1e6个区间,每个区间也就是100个数,只需要存下每个区间的第一个数,查询的时候就能在100次以内推出答案。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=a;i<=b;i++)
#define INF 0x3f3f3f3f
#define N 1000005
#define db double
int n,m,t,mm;
db ans;
template<class T>
inline bool scan_d(T &ret){
char c;
int sgn;
if(c=getchar(),c==EOF) return 0;
while(c!='-'&&(c<'0'||c>'9')) c=getchar();
sgn=(c=='-')?-1:1;
ret=(c=='-')?0:(c-'0');
while(c=getchar(),c>='0'&&c<='9') ret=ret*10+c-'0';
ret*=sgn;
return 1;
}
db f[N];
void init(){
int tt;
for(int i=1;i<=100000000;i++){
if(i%100==1){
tt=i/100+1;
f[tt]=f[tt-1];
}
f[tt]+=1.0/i;
}
}
int main(){
init();
scan_d(t);
For(cas,1,t){
scan_d(n);
m=n/100;
mm=n-100*m;
ans=f[m];
For(i,n-mm+1,n){
ans+=1.0/i;
}
printf("Case %d: %.10f\n",cas,ans);
}
return 0;
}题意:对于给定x,x=y^k,求k的最大值。
算术基本定理分解质因数。。。对所有质因数的幂次求gcd即可。需要注意的是x为负数的情况,可以先去掉负号,与正数一样 处理,这时候若gcd为偶数,则需将gcd除2直到gcd为奇数为止。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define ll long long
#define N 100005
ll t,n,prime[N],cnt,ans;
bool notprime[N];
void init(){
notprime[1]=true;
for(int i=2;i<N;i++){
if(!notprime[i]) prime[cnt++]=i;
for(int j=0;j<cnt&&prime[j]*i<N;j++){
notprime[prime[j]*i]=true;
if(i%prime[j]==0)
break;
}
}
}
ll p[205],e[205],pcnt;
void fenjie(ll x){
memset(e,0,sizeof(e));
pcnt=0;
for(int i=0;i<cnt&&prime[i]<=x;i++){
if(x%prime[i]==0){
p[pcnt]=prime[i];
while(x%prime[i]==0){
x/=prime[i];
e[pcnt]++;
}
pcnt++;
}
}
if(x>1)
p[pcnt]=x,e[pcnt++]++;
}
int main(){
init();
cin>>t;
for(int cas=1;cas<=t;cas++){
cin>>n;
bool flag=0;
if(n<0)
flag=1,n=-n;
fenjie(n);
ans=0;
for(int i=0;i<pcnt;i++){
ans=__gcd(ans,e[i]);
}
if(!flag||ans%2==1)//x是偶数或者gcd是奇数均可直接输出
printf("Case %d: %lld\n",cas,ans);
else{//x是奇数
while(ans%2==0) ans/=2;//若gcd是偶数,则需除2到是奇数为止
printf("Case %d: %lld\n",cas,ans);
}
}
return 0;
}题意:一个很大很大的数,除以一个int型的数,问是否可整除。
思路:通过字符串一位一位转化成数字同时对要除的数取模即可。//我脑子抽了直接上java大数了
import java.util.*;//没错,这是java代码,虽然C艹写这题也很简单,但是我懒的再写一遍了
import java.math.*;
public class Main
{
public static void main(String[] args)
{
Scanner input = new Scanner(System.in);
int t=input.nextInt();
for(int cas=1;cas<=t;cas++){
BigInteger a=input.nextBigInteger();
BigInteger b=input.nextBigInteger();
if(b.compareTo(BigInteger.valueOf(0))<0){
b=b.multiply(BigInteger.valueOf(-1));
a.multiply(BigInteger.valueOf(-1));
}
int ans=a.mod(b).intValue();
if(ans==0){
System.out.println("Case "+cas+": divisible");
}
else
System.out.println("Case "+cas+": not divisible");
}
}
}题意挺好懂,但是还挺难描述的,就不多说了。
这种题一看就是找计算式的,大致一推规律,就可以发现公式sigma(Ai)*k*n^(k-1)%mod,k比较大,上快速幂。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=a;i<=b;i++)
#define INF 0x3f3f3f3f
#define N 1005
#define db double
int n,k,mod,t,ans,s;
template<class T>
inline bool scan_d(T &ret){
char c;
int sgn;
if(c=getchar(),c==EOF) return 0;
while(c!='-'&&(c<'0'||c>'9')) c=getchar();
sgn=(c=='-')?-1:1;
ret=(c=='-')?0:(c-'0');
while(c=getchar(),c>='0'&&c<='9') ret=ret*10+c-'0';
ret*=sgn;
return 1;
}
int qpow(int a,int b){
int res=1;
a%=mod;
while(b){
if(b&1) res=(res*a)%mod;
b>>=1;
a=a*a%mod;
}
return res;
}
int main(){
scan_d(t);
For(cas,1,t){
s=0;
scan_d(n),scan_d(k),scan_d(mod);
For(i,1,n){
scan_d(ans);
ans%=mod;
s=(s+ans)%mod;
}
printf("Case %d: %d\n",cas,qpow(n,k-1)*(k%mod)%mod*s%mod);
}
return 0;
}题意:求a到b区间内素数的个数。
思路:区间素数筛。先预处理素数筛打出素数表,注意必须包括所有可能的sqrt(b),然后通过1到sqrt(b)区间的素数筛去a到b区间的非素数,再遍历数组对素数进行计数。(因为a、b数值太大,数组开不下,需要整体偏移a,即0到b-1)
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
using namespace std;
#define N 100005
#define ll long long
int t,a,b,prime[10005],cnt,ans;
bool noprime[N],notprime[N];
void init(){
notprime[1]=1;
for(int i=2;i<N;i++){
if(!notprime[i]) prime[cnt++]=i;
for(int j=0;j<cnt&&prime[j]*i<N;j++){
notprime[prime[j]*i]=1;
if(i%prime[j]==0)
break;
}
}
}
int main(){
init();
cin>>t;
for(int cas=1;cas<=t;cas++){
cin>>a>>b;
ans=0;
memset(noprime,false,sizeof(noprime));
int qaq=sqrt(b);
for(int i=0;i<cnt&&prime[i]<=qaq;i++){
ll tt=max(2ll,(a-1ll+prime[i])/prime[i]);
for(ll j=tt;prime[i]*j<=b;j++){
noprime[prime[i]*j-a]=true;
}
}
for(int i=0;i<=b-a;i++){
if(!noprime[i])
ans++;
}
if(a==1)
ans--;
printf("Case %d: %d\n",cas,ans);
}
return 0;
}这题xdoj上有类似的xdoj1019 自然数的秘密,我也恰好写过博客点我点我,也就不再多提了。思路就是二分,需要注意无解时会死循环,要想办法判断一下。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=a;i<=b;i++)
#define INF 0x3f3f3f3f
#define N 1005
#define db double
int n,l,r,mid,t,ans,now,f[20],num,cnt;
template<class T>
inline bool scan_d(T &ret){
char c;
int sgn;
if(c=getchar(),c==EOF) return 0;
while(c!='-'&&(c<'0'||c>'9')) c=getchar();
sgn=(c=='-')?-1:1;
ret=(c=='-')?0:(c-'0');
while(c=getchar(),c>='0'&&c<='9') ret=ret*10+c-'0';
ret*=sgn;
return 1;
}
void init(){
f[0]=1;
for(int i=1;f[i-1]<=1e8;i++){
f[i]=f[i-1]*5;
cnt=i;
}
}
int NOF(int x){//num of five
int s=0;
for(int i=1;i<=cnt;i++){
if(f[i]<=x)
s+=x/f[i];
}
return s;
}
int main(){
init();
scan_d(t);
For(cas,1,t){
scan_d(n);
l=5,r=5*n,now=-1,num=0;
while(l<=r){
mid=(l+r)>>1;
num=NOF(mid);
if(num==n){
now=mid;
r=mid-1;
}
else if(l==r){
break;
}
if(num<n){
l=mid+1;
}
else
r=mid-1;
}
printf("Case %d: ",cas);
if(now==-1){
cout<<"impossible\n";
}
else
cout<<now<<"\n";
}
return 0;
}这道题在这套题里过的人数不算少。。。但可能这题的想法恰好是我想不到的,觉得比其他一些过的人少点的还难,挺好的一道题。
题意:转化一下,可以理解为对于给定的n,求x从1到n的G[x]的和,其中G[x]定义为gcd(x,i)(i从1到x-1)的和。
首先,这题与欧拉函数有关。考虑当gcd(n,i)=j时,则有gcd(n/j,i/j)=1,所以gcd(n,i)=j的个数就是gcd(n/j,i/j)=1的个数,而gcd(n/j,i/j)=1的个数自然就是phi[n/j]。
因此一个朴素的想法是打出欧拉函数表,然后打出G[n]表,再求一个前缀和,最后O(1)查询即可。
令G[n]为n对应的所有gcd(n,i)(1<=i<n)的,G[n]打表时如果根号n枚举每个n的所有因子,然后求出G[n]的值,O(nsqrt(n)),n=4e6,这样显然是会超时的。。。所以我们需要枚举所有可能的因子的值i,然后内层循环枚举该因子的倍数n,G[n]+=i*phi[n/i]。打出G[n]的表后再求出前缀和即可。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=a;i<=b;i++)
#define INF 0x3f3f3f3f
#define N 4000000
#define db double
ll gcd[N+5],phi[N+5];
int n;
template<class T>
inline bool scan_d(T &ret){
char c;
int sgn;
if(c=getchar(),c==EOF) return 0;
while(c!='-'&&(c<'0'||c>'9')) c=getchar();
sgn=(c=='-')?-1:1;
ret=(c=='-')?0:(c-'0');
while(c=getchar(),c>='0'&&c<='9') ret=ret*10+c-'0';
ret*=sgn;
return 1;
}
void init(){
For(i,1,N) phi[i]=i;
for(int i=2;i<=N;i+=2) phi[i]/=2;
for(int i=3;i<=N;i+=2){
if(phi[i]==i){
for(int j=i;j<=N;j+=i)
phi[j]=phi[j]/i*(i-1);
}
}
}
void init1(){
For(i,1,(N+1)/2){
for(int j=2*i;j<=N;j+=i){
gcd[j]+=i*phi[j/i];
}
}
For(i,3,N){
gcd[i]+=gcd[i-1];
}
}
int main(){
init();
init1();
while(scan_d(n),n){
cout<<gcd[n]<<"\n";
}
return 0;
}没看题。。。以后再说
同P
题意:给定u,v,m,n,L,求(m-n)*x=v-u (%L),即求(m-n)*x-L*y=v-u。这里我们可以通过扩展欧几里得解同余方程。
但是我第一次写的因为取模的问题写出了一个bug(居然也AC了),当然后来发现了。。。
第一遍写的:
#include<iostream>
#include<algorithm>
#include<cstdlib>
#include<cstdio>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=a;i<=b;i++)
#define INF 0x3f3f3f3f
#define N 1005
#define db double
ll n,m,x0,y0,L,ans,gc;
template<class T>
inline bool scan_d(T &ret){
char c;
int sgn;
if(c=getchar(),c==EOF) return 0;
while(c!='-'&&(c<'0'||c>'9')) c=getchar();
sgn=(c=='-')?-1:1;
ret=(c=='-')?0:(c-'0');
while(c=getchar(),c>='0'&&c<='9') ret=ret*10+c-'0';
ret*=sgn;
return 1;
}
ll exgcd(ll a,ll b,ll &x,ll &y){
if(b==0){
x=1,y=0;return a;
}
ll d=exgcd(b,a%b,x,y);
int t=x;x=y,y=t-a/b*y;
return d;
}
ll solve(ll a,ll b,ll n,ll gc){
ll x,y,k=b/gc;
exgcd(a,n,x,y);
return (k*x%(L/gc)+L/gc)%(L/gc);//这个地方有点小问题,13 645 31 23 1000会输出-46而不是79
}
int main(){
cin>>x0>>y0>>m>>n>>L;
L=-L;
if(m==n||(y0-x0)%(gc=__gcd(m-n,L)))
cout<<"Impossible\n",exit(0);
ans=solve(m-n,y0-x0,L,gc);
cout<<ans<<endl;
return 0;
}第二遍取模时进行了处理,当L/gc为负数时,为保证结果是正数,需要加应该是-L/gc。
#include<iostream>
#include<algorithm>
#include<cstdlib>
#include<cstdio>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=a;i<=b;i++)
#define INF 0x3f3f3f3f
#define N 1005
#define db double
ll n,m,x0,y0,L,ans,gc;
template<class T>
inline bool scan_d(T &ret){
char c;
int sgn;
if(c=getchar(),c==EOF) return 0;
while(c!='-'&&(c<'0'||c>'9')) c=getchar();
sgn=(c=='-')?-1:1;
ret=(c=='-')?0:(c-'0');
while(c=getchar(),c>='0'&&c<='9') ret=ret*10+c-'0';
ret*=sgn;
return 1;
}
ll exgcd(ll a,ll b,ll &x,ll &y){
if(b==0){
x=1,y=0;return a;
}
ll d=exgcd(b,a%b,x,y);
int t=x;x=y,y=t-a/b*y;
return d;
}
ll solve(ll a,ll b,ll n,ll gc){
ll x,y,k=b/gc;
exgcd(a,n,x,y);
if(L/gc>0)
return (k*x%(L/gc)+(L/gc))%(L/gc);
else
return ((k*x)%(L/gc)+(-L/gc))%(L/gc);
}
int main(){
cin>>x0>>y0>>m>>n>>L;
L=-L;
if(m==n||(y0-x0)%(gc=__gcd(m-n,L)))
cout<<"Impossible\n",exit(0);
ans=solve(m-n,y0-x0,L,gc);
cout<<ans<<endl;
return 0;
}题意:已知A,B,C,k,解C*x=B-A (% 2^k)同余方程。
和前一题青蛙的约会有点类似,因此可以扩展欧几里得来求解。
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=a;i<=b;i++)
ll f[40],a,b,c,gc,t,ans;
int k;
void init(){//预先存的负值,方便之后使用
f[0]=-1;
For(i,1,32){
f[i]=f[i-1]*2;
}
}
void exgcd(ll a,ll b,ll &x,ll &y){
if(b==0) x=1,y=0;
else
exgcd(b,a%b,x,y),t=x,x=y,y=t-a/b*y;
}
ll solve(ll a,ll b,ll c){
ll x,y,k=c/gc,tt1=b/gc,tt=b/gc;
exgcd(a,b,x,y);
if(tt<0)
tt1=-tt;
return (k*x%tt+tt1)%tt;
}
int main(){
init();
while(cin>>a>>b>>c>>k,a||b||c||k){
//c*x=b-a(%2^k) c*x-f[k]*y=b-a
gc=__gcd(c,f[k]);
if((b-a)%gc!=0){
cout<<"FOREVER\n";
}
else{
ans=solve(c,f[k],b-a);
cout<<ans<<endl;
}
}
return 0;
} 题意:用斐波那契数列表示数x,若x=f[2]+f[0],则x可以表示为101。用没有相邻的1的斐波那契表示法表示数x和y,并对它们的和同样用没有相邻的1的斐波那契表示法表示。
这题算是贪心?可以想到一个结论,假设某个数从它所能包含的最大的斐波那契数开始表示,那么一定没有相邻的1。为什么呢?假设该数的某个表示含有两个相邻的1——即f[j]和f[j-1],那么这两位一定可以用f[j+1]来表示,我们的贪心使其变为了1位;若有f[j]、f[j-1]、f[j-2],则显然会变为f[j+1]、f[j-2],不再相邻。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=a;i<=b;i++)
#define INF 0x3f3f3f3f
#define N 105
#define db double
ll f[N],tt;
char ac[N],bc[N];
void init(){
f[0]=1,f[1]=2;
For(i,2,40) f[i]=f[i-1]+f[i-2];
}
struct node{
char cnum[N];
ll num,ws;
int kg;
}a,b,c;
void cal(node &aa){
aa.ws=strlen(aa.cnum)-1,aa.num=0;
for(int i=aa.ws;i>=0;i--){
aa.num+=(aa.cnum[i]-'0')*f[aa.ws-i];
}
}
void incal(node &aa){
tt=aa.num,aa.ws=-1;
for(int i=40;i>=0;i--){
if(tt>=f[i]){
tt-=f[i],aa.cnum[++aa.ws]='1';
}
else if(aa.ws>=0||i==0)
aa.cnum[++aa.ws]='0';
}
aa.cnum[aa.ws+1]='\0';
}
void print(node aa){
For(i,1,aa.kg) cout<<" ";
cout<<aa.cnum<<"\n";
}
int main(){
init();
while(cin>>a.cnum>>b.cnum){//按fib数列由大至小分解出来的1一定两两不相邻
//因为若某个数分解后出现俩个相邻的1,则这两位加起来可以由更大的一位表示!
cal(a),cal(b),c.num=a.num+b.num;
incal(c),incal(a),incal(b);
c.kg=2,a.kg=c.ws-a.ws+2,b.kg=c.ws-b.ws+1;
print(a),cout<<"+",print(b);
For(i,1,c.kg) cout<<" ";
For(i,1,c.ws+1) cout<<"-";
cout<<"\n";
print(c);
cout<<"\n";
}
return 0;
}题意:判断一个数是不是素数。数范围很小,个数也不多,根号n的复杂度暴力判断或者预处理素数筛都行。
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int n;
bool f(int t){
if(t==1||t==2)
return false;
for(int i=2;i<=sqrt(t);i++){
if(t%i==0)
return false;
}
return true;
}
int main(){
int d=1;
while(scanf("%d",&n)){
if(n<=0)
break;
if(f(n)){
cout<<d<<": yes\n";
}
else
cout<<d<<": no\n";
d++;
}
return 0;
}题意:对给定的一堆数字求两两之间最大的gcd值。
不得不说,这输入真是毒瘤。。。因为不清楚每组数据究竟有多少个数,先以字符串形式读入一行,再处理成对应的数。
因为数据量不大,直接两两求gcdO(n^2)暴力即可。
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
int a[110];
int gcd(int l,int b){
return b==0?l:gcd(b,l%b);
}
int main(){
int n;
char c;
cin>>n;
getchar();
while(n--){
memset(a,0,sizeof(a));
int num=0,flag=0;
while(scanf("%c",&c)){
if(c=='\n'){
if(flag==0)
num++;
break;
}
if(c>='0'&&c<='9'){
a[num]=a[num]*10+c-'0';
flag=0;
}
else if(c==' '&&flag==0){
flag=1;
num++;
}
}
int ans=0;
for(int i=0;i<num-1;i++){
for(int j=i+1;j<num;j++){
ans=max(ans,gcd(a[i],a[j]));
}
}
cout<<ans<<endl;
}
return 0;
}题意:求[a,b]区间内i*i+i+41为素数所占的比例,保留两位小数。
方法很简单,因为数据量不大,直接预处理出素数个数的前缀和,然后算一下就好。然而!!!这里一个大问题,精度。。。求dalao告知为啥最后要加点东西才能过。。。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=a;i<=b;i++)
#define INF 0x3f3f3f3f
#define N 1005
#define db double
int a,b,tt,tat,ans;
template<class T>
inline bool scan_d(T &ret){
char c;
int sgn;
if(c=getchar(),c==EOF) return 0;
while(c!='-'&&(c<'0'||c>'9')) c=getchar();
sgn=(c=='-')?-1:1;
ret=(c=='-')?0:(c-'0');
while(c=getchar(),c>='0'&&c<='9') ret=ret*10+c-'0';
ret*=sgn;
return 1;
}
bool flag;
int sum[10005];
void init(){
sum[0]=1;
For(i,1,10000){
if(i<40){
sum[i]=sum[i-1]+1;
continue;
}
tt=i*i+i+41,tat=sqrt(tt),flag=1;
For(j,2,tat){
if(tt%j==0){
flag=0;
break;
}
}
sum[i]=sum[i-1]+flag;
}
}
int main(){
init();
while(cin>>a>>b){
db fz=sum[b]-(a==0?0:sum[a-1]),fm=(b-a+1);
printf("%.2lf\n",fz/fm*100+1e-5);//+1e-5,1e-6,1e-8,1e-10,1e-12都行,1e-4不行,其他没试
}
return 0;
}题意:求法里数列的个数。法里数列定义啥的看原题。
很容易想到,第n项新增的法里数列的个数是与n互质的数的个数,也就是欧拉函数phi[n],预处理前缀和即可。
#include<iostream>
#include<cstdio>
using namespace std;
#define ll long long
#define For(i,a,b) for(int i=a;i<=b;i++)
#define INF 0x3f3f3f3f
#define N 1000000
#define db double
int n,m,t,ans,phi[N+5];
ll f[N+5];
template<class T>
inline bool scan_d(T &ret){
char c;
int sgn;
if(c=getchar(),c==EOF) return 0;
while(c!='-'&&(c<'0'||c>'9')) c=getchar();
sgn=(c=='-')?-1:1;
ret=(c=='-')?0:(c-'0');
while(c=getchar(),c>='0'&&c<='9') ret=ret*10+c-'0';
ret*=sgn;
return 1;
}
void getphi(){
For(i,1,N) phi[i]=i;
for(int i=2;i<=N;i+=2) phi[i]/=2;
for(int i=3;i<=N;i+=2){
if(phi[i]==i){
for(int j=i;j<=N;j+=i){
phi[j]=phi[j]/i*(i-1);
}
}
}
}
void getf(){
f[2]=1;
For(i,3,N){
f[i]=f[i-1]+phi[i];
}
}
int main(){
getphi();
getf();
while(scan_d(n),n){
cout<<f[n]<<endl;
}
return 0;
}题意:按大小顺序输出1到(2^64)-1的所有"super power number",其中"super power number"的定义是能表示成x^y和m^n,其中x>0&&m>0&&y>1&&n>1。
由算术基本定理,可以想到,将num分解质因数后,若所有幂次的gcd不为质数,则gcd至少含有两个非1因子,即num至少可表示x^y和m^n两种形式,其中gcd%y==0&&gcd%n==0。
上述情况即为满足条件的数,那么我们可以开始构造,先特判加上1,枚举底数i从2到sqrt(sqrt(2^64 -1))也就是65535——因为至少4次幂才满足条件——循环内部再枚举每个底数的幂次numi和幂数j,如果numi是非质数就把j存起来,即为一个满足条件的数,注意2^64-1恰好是unsigned long long所能表示的最大数值,因此要防止溢出。枚举完毕后再排个序即可。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
#define For(i,a,b) for(int i=a;i<=b;i++)
#define INF 0x3f3f3f3f
#define N 4000000
#define db double
int cnt,prime[100];
bool np[100];
void Prime(){
np[1]=1;
For(i,2,90){
if(!np[i]) prime[cnt++]=i;
for(int j=0;j<cnt&&prime[j]*i<=90;j++){
np[prime[j]*i]=1;
if(i%prime[j]==0) break;
}
}
}
map<ull,bool> mp;
void init(){
ull maxnum=1;
For(i,1,63){
maxnum*=2;
}
maxnum+=(maxnum-1);
mp.insert(make_pair(1,true));
int tt=65535;
ull tt1,j,numi;
For(i,2,tt){
j=i*1ull*i*i*i,numi=4;
while(1){
if(numi>=4&&np[numi]) mp[j]=true;
if(j<=maxnum/i) j*=i,numi++;//此处防止溢出,不可能等到j大于2^64-1再判断,因此要提前一点判断。
else break;
}
}
}
int main(){
Prime();
init();
map<ull,bool>::iterator it=mp.begin();
for(;it!=mp.end();it++){
cout<<it->first<<"\n";
}
return 0;
}其余三题估计短时间内不会补