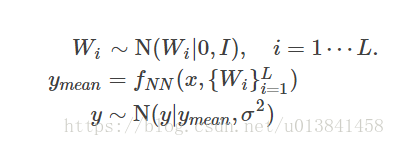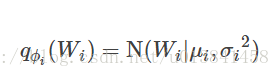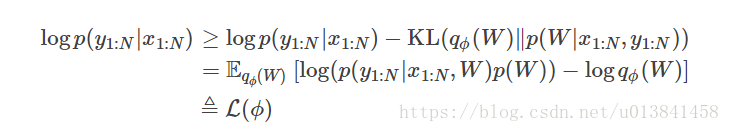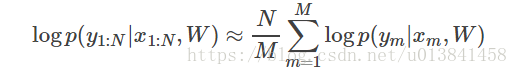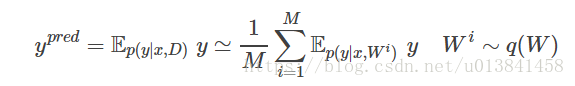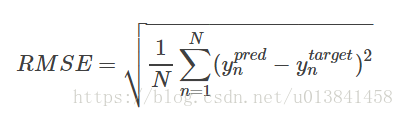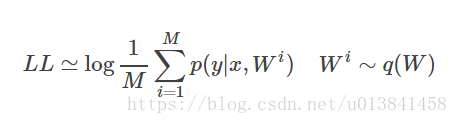Bayesian Neural Networks for Regression解析

地址：https://zhusuan.readthedocs.io/en/latest/tutorials/bayesian_nn.html

本教程假设读者已经熟悉了ZhuSuan的基本概念。

近年来神经网络在拟合复杂变换方面具有强大的能力，成功应用于语音识别，图像分类和机器翻译等。然而，神经网络的典型训练需要大量标记数据来控制过度拟合的风险。 当涉及现实世界的回归任务时，问题变得更加困难。 这些任务通常需要使用较小的训练数据，这些数据的高频特性常常使神经网络更容易陷入过度拟合中。

解决该问题的原理方法是贝叶斯神经网络（BayesianNN）。 在BayesianNN中，先前的分布被放在神经网络的权重上以考虑建模不确定性。 通过对权重进行贝叶斯推断，可以学习既适合训练数据又知道自己对测试数据的预测的不确定性的预测器。 在本教程中，我们将展示如何在ZhuSuan中实现BayesianNN。 本教程的完整脚本位于examples / bayesian_neural_nets / bayesian_nn.py中。

我们使用名为Boston housing的回归数据集。 这具有N = 506个数据点，D = 13维。 用于建模多元回归的BayesianNN的转发过程如下：

该转发过程以输入特征（x）开始，然后x通过具有L层的深度神经网络（fNN）转发，其在每层（Wi）中的参数满足分解的多元标准正态分布。 通过这种复杂的转发过程，模型可以学习输入（x）和输出（y）之间的复杂关系。 最后，将一些噪声添加到输出中以获得模型的易处理可能性，这通常是回归问题中的高斯噪声。 贝叶斯神经网络的图形模型表示如下。

 

Build the Model

在转发过程之后，首先我们需要标准的正态分布来生成权重（{Wi} Li = 1）。 对于具有n_in输入单位和n_out输出单位的图层，权重的形状为[n_out，n_in + 1]（偏差的另一列）。 如我们的图形模型所示，权重的潜在变量对于所有数据都是全局的。 所以我们只需要它们的一个副本，也就是说，我们需要一个形状为[1，n_out，n_in + 1]的Normal StochasticTensor：

with zs.BayesianNet(observed=observed) as model:
    ws = []
    for i, (n_in, n_out) in enumerate(zip(layer_sizes[:-1],
                                          layer_sizes[1:])):
        w_mu = tf.zeros([1, n_out, n_in + 1])
        ws.append(
            zs.Normal('w' + str(i), w_mu, std=1.,
                      n_samples=n_particles, group_ndims=2))

 要将每个图层中的权重作为一个整体处理并评估它们的概率，group_ndims设置为2.如果您不熟悉此属性，请参阅Distribution和StochasticTensor。

然后我们编写神经网络的前馈过程，通过它建立输出y和输入x之间的连接：

with zs.BayesianNet(observed=observed) as model:
    ...
    # forward
    ly_x = tf.expand_dims(
        tf.tile(tf.expand_dims(x, 0), [n_particles, 1, 1]), 3)
    for i in range(len(ws)):
        w = tf.tile(ws[i], [1, tf.shape(x)[0], 1, 1])
        ly_x = tf.concat(
            [ly_x, tf.ones([n_particles, tf.shape(x)[0], 1, 1])], 2)
        ly_x = tf.matmul(w, ly_x) / \
            tf.sqrt(tf.to_float(tf.shape(ly_x)[2]))
        if i < len(ws) - 1:
            ly_x = tf.nn.relu(ly_x)

接下来，我们在评估概率时添加观察分布（噪声）以获得易处理的可能性：

with zs.BayesianNet(observed=observed) as model:
    ...
    y_mean = tf.squeeze(ly_x, [2, 3])
    y_logstd = tf.get_variable(
        'y_logstd', shape=[],
        initializer=tf.constant_initializer(0.))
    y = zs.Normal('y', y_mean, logstd=y_logstd)

组合并添加模型重用，构建BayesianNN的代码是：

import tensorflow as tf
import zhusuan as zs

@zs.reuse('model')
def bayesianNN(observed, x, n_x, layer_sizes, n_particles):
    with zs.BayesianNet(observed=observed) as model:
        ws = []
        for i, (n_in, n_out) in enumerate(zip(layer_sizes[:-1],
                                              layer_sizes[1:])):
            w_mu = tf.zeros([1, n_out, n_in + 1])
            ws.append(
                zs.Normal('w' + str(i), w_mu, std=1.,
                          n_samples=n_particles, group_ndims=2))

        # forward
        ly_x = tf.expand_dims(
            tf.tile(tf.expand_dims(x, 0), [n_particles, 1, 1]), 3)
        for i in range(len(ws)):
            w = tf.tile(ws[i], [1, tf.shape(x)[0], 1, 1])
            ly_x = tf.concat(
                [ly_x, tf.ones([n_particles, tf.shape(x)[0], 1, 1])], 2)
            ly_x = tf.matmul(w, ly_x) / \
                tf.sqrt(tf.to_float(tf.shape(ly_x)[2]))
            if i < len(ws) - 1:
                ly_x = tf.nn.relu(ly_x)

        y_mean = tf.squeeze(ly_x, [2, 3])
        y_logstd = tf.get_variable(
            'y_logstd', shape=[],
            initializer=tf.constant_initializer(0.))
        y = zs.Normal('y', y_mean, logstd=y_logstd)

    return model, y_mean

Inference

构建模型后，下一步是推断后验分布或给定训练数据的权重的不确定性。

 

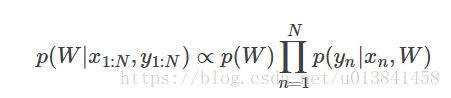
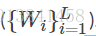
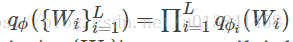
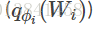
由于归一化常数是难以处理的，我们无法直接计算网络参数的后验分布。 为了解决这个问题，我们使用变分推理，即使用变分分布来逼近真实的后验。 我们可以指定的最简单的变分后验是分解的（也称为平均场）正态分布由其均值和对数标准差参数化。

def mean_field_variational(layer_sizes, n_particles):
    with zs.BayesianNet() as variational:
        ws = []
        for i, (n_in, n_out) in enumerate(zip(layer_sizes[:-1],
                                              layer_sizes[1:])):
            w_mean = tf.get_variable(
                'w_mean_' + str(i), shape=[1, n_out, n_in + 1],
                initializer=tf.constant_initializer(0.))
            w_logstd = tf.get_variable(
                'w_logstd_' + str(i), shape=[1, n_out, n_in + 1],
                initializer=tf.constant_initializer(0.))
            ws.append(
                zs.Normal('w' + str(i), w_mean, logstd=w_logstd,
                          n_samples=n_particles, group_ndims=2))
    return variational

在变分推断中，使qφ（W）近似为p（W | x1：N，y1：N）。 我们需要最大化边际对数概率的下限（logp（y | x））：

当且仅当qφ（W）= p（W | x1：N，y1：N）时，下限等于边际对数似然，对于i在1 ... L，当它们之间的Kullback-Leibler发散时为零。

这个下界通常称为证据下界（ELBO）。 请注意，我们需要评估的唯一概率是联合可能性和变分后验的概率。 对数条件可能性是

计算整个数据集的日志条件似然非常耗时。 在实践中，我们对小批量数据进行子采样以近似条件似然

这里{（xm，ym）} m = 1：M是包括来自训练集{（xn，yn）} n = 1：N的M个随机样本的子集。 M称为批量大小。 通过将批量大小设置得相对较小，我们可以有效地计算上述公式。 此外，使用迷你批次带来额外的好处。 由于优化算法的一般问题是参数可能陷入局部最小值。 使用小批量带来随机性，这增加了算法跳出局部最小值的机会。

note：与VAE等其他一些模型不同，贝叶斯NN的潜在变量{Wi} Li = 1对于所有数据都是全局的，因此我们没有明确地对变量后验中的每个数据进行W条件。

我们通过随机梯度下降来优化这个下界。 正如我们在VAE教程中所做的那样，使用随机梯度变分贝叶斯（SGVB）估计器。 这部分的代码是：

n_particles = tf.placeholder(tf.int32, shape=[], name='n_particles')
x = tf.placeholder(tf.float32, shape=[None, n_x])
y = tf.placeholder(tf.float32, shape=[None])
layer_sizes = [n_x] + n_hiddens + [1]
w_names = ['w' + str(i) for i in range(len(layer_sizes) - 1)]

def log_joint(observed):
    model, _ = bayesianNN(observed, x, n_x, layer_sizes, n_particles)
    log_pws = model.local_log_prob(w_names)
    log_py_xw = model.local_log_prob('y')
    return tf.add_n(log_pws) + log_py_xw * N

variational = mean_field_variational(layer_sizes, n_particles)
qw_outputs = variational.query(w_names, outputs=True,
                               local_log_prob=True)
latent = dict(zip(w_names, qw_outputs))
lower_bound = zs.variational.elbo(
    log_joint, observed={'y': y}, latent=latent, axis=0)
cost = tf.reduce_mean(lower_bound.sgvb())
lower_bound = tf.reduce_mean(lower_bound)

optimizer = tf.train.AdamOptimizer(learning_rate=0.01)
infer_op = optimizer.minimize(cost)

 Evaluation

我们上面所做的是定义模型并推断参数。 这样做的主要目的是预测新数据。 给定其输入特征（x）和我们的训练数据（D）的新数据（y）的概率分布是

 

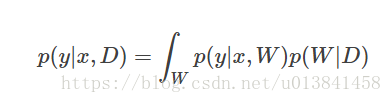
因为我们已经通过变分后验q（W）学习了p（W | D）的近似，我们可以将它代入方程

尽管上述积分仍然难以处理，但蒙特卡罗估计可用于通过从变分后验中采样来获得无偏估计

我们可以选择这种预测分布的均值作为我们对新数据的预测

首先，我们需要将数据占位符和采样的潜在参数传递给BayesianNN模型

# prediction: rmse & log likelihood
observed = dict((w_name, latent[w_name][0]) for w_name in w_names)
observed.update({'y': y})
model, y_mean = bayesianNN(observed, x, n_x, layer_sizes,
                           n_particles)

预测均值由y_mean给出。 为了了解其性能，我们希望计算一些定量测量，包括均方根误差（RMSE）和对数似然。

RMSE定义为预测均方误差的平方根，较小的RMSE意味着更好的预测准确度：

对数似然（LL）定义为似然函数的自然对数，较大的LL表示学习模型更好地拟合测试数据：

这也可以通过蒙特卡罗估计来计算 

需要注意的是，由于我们通常将数据标准化以使它们在开始时具有单位方差（检查完整的脚本示例/ bayesian_neural_nets / bayesian_nn.py），我们需要在我们的评估公式中计算其效果。 RMSE与幅度成正比，因此最终的RMSE应乘以标准偏差。 对于对数似然，需要将其减去日志项。 总之，评估代码是：

# prediction: rmse & log likelihood
observed = dict((w_name, latent[w_name][0]) for w_name in w_names)
observed.update({'y': y})
model, y_mean = bayesianNN(observed, x, n_x, layer_sizes,
                           n_particles)
y_pred = tf.reduce_mean(y_mean, 0)
rmse = tf.sqrt(tf.reduce_mean((y_pred - y) ** 2)) * std_y_train
log_py_xw = model.local_log_prob('y')
log_likelihood = tf.reduce_mean(zs.log_mean_exp(log_py_xw, 0)) - \
    tf.log(std_y_train)

 Run Gradient Descent

再次，一切运行良好之前。 现在添加以下代码以运行训练循环并查看贝叶斯神经网络如何执行：

# Run the inference
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for epoch in range(1, epochs + 1):
        lbs = []
        for t in range(iters):
            x_batch = x_train[t * batch_size:(t + 1) * batch_size]
            y_batch = y_train[t * batch_size:(t + 1) * batch_size]
            _, lb = sess.run(
                [infer_op, lower_bound],
                feed_dict={n_particles: lb_samples,
                           x: x_batch, y: y_batch})
            lbs.append(lb)
        print('Epoch {}: Lower bound = {}'
              .format(epoch, np.mean(lbs)))

        if epoch % test_freq == 0:
            test_lb, test_rmse, test_ll = sess.run(
                [lower_bound, rmse, log_likelihood],
                feed_dict={n_particles: ll_samples,
                           x: x_test, y: y_test})
            print('>> TEST')
            print('>> lower bound = {}, rmse = {}, log_likelihood '
                  '= {}'.format(test_lb, test_rmse, test_ll))