05 Neural Networks

Neural Networks

The ‘one learning algorithm’ hypothesis

1. Neuron-rewiring experiments

Model Representation

Define

1. Sigmoid(logistic) activation function
2. bias unit
3. input layer
4. output layer
5. hidden layer
6. \(a_i^{(j)}\) : ‘activation’ of unit \(i\) in layer \(j\)
7. \(\theta^{(j)}\): matrix of weights controlling function mapping from layer \(j\) to layer \(j + 1\).

Calculate

\[a^{(j)} = g(z^{(j)})\]
\[g(x) = \frac{1}{1 + e^{-x}}\]
\[z^{(j + 1)} = \Theta^{(j)}a^{(j)}\]
\[h_\theta(x) = a^{(j + 1)} = g(z^{(j + 1)})\]

Cost Function

\[
J(\Theta) = - \frac{1}{m} \sum_{i=1}^m \sum_{k=1}^K \left[y^{(i)}_k \log ((h_\Theta (x^{(i)}))_k) + (1 - y^{(i)}_k)\log (1 - (h_\Theta(x^{(i)}))_k)\right] + \]

\[\frac{\lambda}{2m}\sum_{l=1}^{L-1} \sum_{i=1}^{s_l} \sum_{j=1}^{s_{l+1}} ( \Theta_{j,i}^{(l)})^2
\]

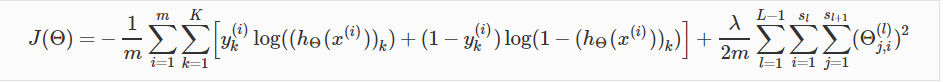
Back-propagation Algorithm

Algorithm

1. Hypothesis we have calculated all the \(a^{(l)}\) and \(z^{(l)}\)
2. set \(\Delta^{(l)}_{i, j} := 0\) for all (l, i, j)
3. using \(y^{(t)}\), compute \(\delta^{L} = a^{(L)} - y^{(t)}\), where \(y^{(t)}_{k}(i) \in {0, 1}\) indicates whether the current training example belongs to class k{\(y^{(t)}_{k}(k) = 1\)}, or if it belongs to a different class = 0;
4. For the hidden layer \(l = L - 1\) down to 2, set
   \[
   \delta^{(l)} = (\Theta^{(l)})^T\delta^{(l + 1)} .* g’(z^{(l)})
   \]
5. remember remove \(\delta_0^{(l)}\) by. delta(2:end)
   \[
   \Delta^{(l)} = \Delta^{(l)} + \delta^{(l + 1)}(a^{(l)})^T
   \]
6. gradient
   \[
   \frac{\partial}{\partial\Theta^{(l)}_{i,j}}J(\Theta) = D^{(l)}_{i,j} = \frac{1}{m}\Delta^{(l)}_{i,j} +
   \begin{cases} \frac{\lambda}{m}\Theta^{(l)}_{i, j}, & \text {if j $\geq$ 1} \\ 0, & \text{if j = 0} \end{cases}
   \]

Gradient Checking

1. \[
   \frac{d}{d\Theta}J(\Theta) \approx \frac{J(\Theta + \epsilon) - J(\Theta - \epsilon)}{2\epsilon}
   \]
2. A small value for \(\epsilon\) such as \(\epsilon = 10^{-4}\)
3. check that gradApprox \(\approx\) deltalVector

4.

epsilon = 1e-4;
for i = 1 : n
    thetaPlus = theta;
    thetaPlus(i) += epsilon;
    thetaMinus = theta;
    thetaMinus(i) -= epsilon;
    gradApprox(i) = (J(thetaPlus) - J(thetaMinus)) / (2 * epsilon);
end;

Rolling and Unrolling

Random Initialization

Theta = rand(n, m)) * (2 * INIT_EPSILON) - INIT_EPSILON;

1. initialize \( \Theta^{(l)}_{ij} \in [-\epsilon, \epsilon] \)
2. else if we initializing all theta weights to zero, all nodes will update to the same value repeatedly when we back_propagate.
3. One effective strategy for choosing \(\epsilon_{init}\) is to base the number of units in the network. A good choice of \(\epsilon_{init}\) is \(\epsilon_{init} = \frac{\sqrt{6}}{\sqrt{L_{in} + L_{out}}} \)

Training a Neural Network

1. Randomly initialize weights

    Theta = rand(n, m) * (2 * epsilon) - epsilon;

1. Implement forward propagation to get \(h_\Theta(x^{(i)})\) for any \(x^{(i)}\)
2. Implement code to compute cost function \(J(\Theta)\)

3. Implement back-prop to compute partial derivatives \( \frac{d(J\Theta)}{d\Theta_{jk}^{(l)}} \)

   • \( g’(z) = \frac{d}{dz}g(z) = g(z)(1 - g(z))\)
   • \( sigmoid(z) = g(z) = \frac{1}{1 + e^{-z}}\)

4. Use gradient checking to compare \( \frac{d(J\Theta)}{d\Theta_{jk}^{(l)}} \) computed using back-propagation vs. using numerical estimate of gradient of \(J(\Theta)\)
   Then disable gradient checking code

5. Use gradient descent or advanced optimization method with back-propagation to try to minimize \(J(\Theta)\) as a function of parameters \(\Theta\)