LCA（Lobe Component Analysis）：叶成分分析

前面提到的CCIPCA可以算作翁巨扬教授提出的第一个心智发育框架IHDR的核心算法，而LCA则是他现阶段提出的where-what-network框架的核心算法，也即是他提到的发育网络的“基因”组成。

CCIPCA对应于PCA（主成分分析）算法，是PCA算法的增强版，使得计算算法在计算判别空间的特征向量时，covariance-free，且学习过程为在线增量式的学习。CCILCA则对应于ICA（独立成分分析），是ICA算法的增强版。这里说明一下，主成分分析与独立成分分析的最大不同之处在于：PCA得到的特征向量是彼此之间相互正交的，也即是正交分解，ICA得到的特征向量则不必两两间正交，实际上，特征向量也不必满足严格正交关系。

1、叶成分

假设有C个神经元，LCA将样本空间 $\chi$ 划分为C个互相不重叠的区域，也即是叶区域：

$\chi =R_{1}\bigcup R_{2}\bigcup ...\bigcup R_{C}...........................(1)$

其中，叶区域之间两两不相交，每一个叶区域采用一个单位特征向量 $v_{i}$ 表示，这些特征向量不需要彼此之间正交或线性独立，他们就形成了一个叶特征子空间 $S$ ：

$S = span\left \{ v_{1} , v_{2}, ..., v_{C}\right \}............................(2)$

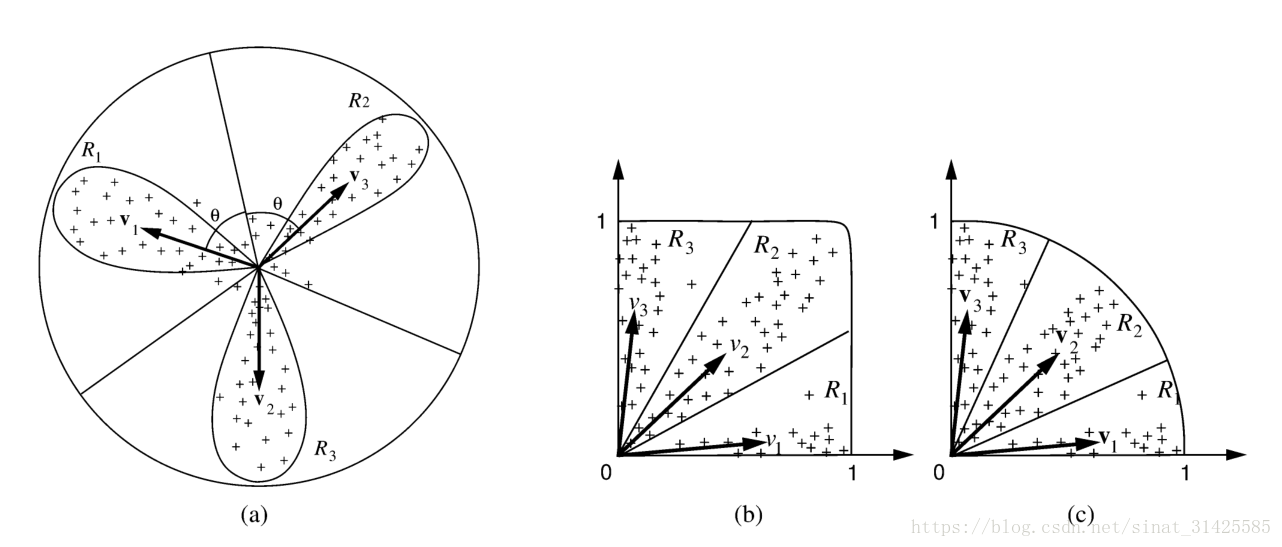
如果样本X的分布为一个方差为1的高斯分布，样本将在所有方向都存在相同密度。通常，样本的分布不是高斯分布，概率密度集中在某一个方向，每一个主要的聚集方向，称之为一个lobe，如图1所示。

图1 叶成分（摘自文献Dually Optimal Neuronal Layers: Lobe Component Analysis）

2、叶成分对应最优的空间表示

首先，假定所有的C个叶区域 $\left \{ R_{1},R_{2}, ... ,R_{C} \right \}$ 都已经给定，来推导最优表征；然后，我们对叶区域进行更新，对叶区域进行调整。

假设一个样本输入X属于叶区域 $R_{i}$ ，我们希望使用 $R_{i}$ 对应的特征向量 $v_{i}$ 来表示，即 $X\approx\alpha v_{i}$ ，使得近似误差 $E\left \| X-\alpha v_{i} \right \|^{2}$ 最小，这个时候，最优解为： $\alpha =X\cdot v_{i}$ ，这个时候 $X\approx \left ( X\cdot v_{i} \right )v_{i}$ 。

那么，对于C个叶区域而言，全局的最小近似误差为：

$R_{j}=\left \{ X| j = argmin(X-\left ( X\cdot v_{i} \right )v_{i}) \right \},i=1,2,...,C..........................(3)$

反过来，如果我们已知样本输入X属于叶区域 $R_{i}$ ，那么采用怎样的特征向量 $v_{i}$ 来最优地表征该叶区域，表征X的平方近似误差为：

$\left \|X- \left ( X\cdot v_{i} \right )v_{i} \right \|^{2}=\left (X- \left ( X\cdot v_{i} \right )v_{i} \right )^{T}\left (X- \left ( X\cdot v_{i} \right )v_{i} \right )$

$=X^{T}X-v_{i}^{T}Xv_{i}^{T}X-X^{T}(X\cdot v_{i})v_{i} + (X\cdot v_{i})v_{i}^{T} (X\cdot v_{i})v_{i}$

$= X^{T}X-X^{T} v_{i}v_{i}^{T}X-X^{T}(X^{T} v_{i})v_{i} + (X^{T} v_{i})v_{i}^{T} (X^{T}v_{i})v_{i}$

$= X^{T}X-X^{T} v_{i}v_{i}^{T}X-X^{T}X^{T} v_{i}v_{i} + X^{T} v_{i}v_{i}^{T} X^{T}v_{i}v_{i}$

$= X^{T}X-X^{T} v_{i}v_{i}^{T}X-X^{T}X^{T} v_{i}v_{i} + X^{T} X^{T}v_{i}v_{i}$

$= X^{T}X-(v_{i}^{T}X)^{T}(v_{i}^{T}X) =X^{T}X-(X^{T}v_{i})^{T}(X^{T}v_{i})$

最后一步能交换的原因为 $X^{T}v_{i}=v_{i}^{T}X$ 表示一个标量，那么，对于叶区域 $R_{i}$ 近似误差的期望值为：

$E\left \|X- \left ( X\cdot v_{i} \right )v_{i} \right \|^{2} =E[X^{T}X]-v_{i}^{T}E[X^{T}X]v_{i}=trace(\sum_{x}) - v_{i}^{T}\sum_{x}v_{i}........(4)$

注意，第一个分量为常量，如果要最小化近似误差的期望值，需要最大化第二个部分，从主成分分析的角度来看，即 $v_{i}$ 取值为协方差矩阵最大特征值对应特征向量，有：

$\lambda v_{i}=\sum_{x}v_{i}.....................(5)$

两边乘以 $v_{i}^{T}$ ，有：

$\lambda= v_{i}^{T} \sum_{x}v_{i}=E(X\cdot v_{i})^{2}..........(6)$

从上面分析可得，当样本X表示的方向与所处叶区域 $R_{i}$ 对应方向越相近时，对应全局的近似误差越小。空间最优对应于表征误差最小。更直观一些的表述就是，如果我先用前C个样本初始化C个叶区域对应特征向量，第C+1个样本到来时，我就在前C个特征向量中选取与当前样本方向最一致的特征向量来表征该样本，这样就可以使得当前步骤对应全局最小近似误差，然后，如果我们能保障每一步都是全局最小近似误差，就可以达到整体的最小表征误差。

3、时间最优：LCA对应最优的学习步长

为了处理长期记忆和快速自适应规则，我们需要对问题的解进行增量式地优化，受生物突触学习的启发，假设对于LCA而言，神经内部的观测量(neuronal internal observation (NIO))定义为响应权重的输入：

$u(t) =\frac{x(t)\cdot v(t-1)}{\left \| v(t-1) \right \|}x(t).............................(7)$

突触权重向量 $v(t)$ 是对一系列的观测量 $U(t)=\left \{ u_{1} ,u_{2},...,u_{n}\right \}$ 评估得到的。假设在第t个时刻，NIO的学习率为 $\eta _{t}$ ，那么我们如何来自动的设定学习率 $\left \{ \eta _{1},\eta _{2},...,\eta _{n} \right \}$ ，使得在每一个时刻对于神经权重向量 $\hat{v}(t)$ 的评估值误差最小，这意味着，在每一个时刻t更新，使得：

$minimum-error(t)=\left \| \hat{v}(U(t))-v^{*} \right \|^{2}..........................(8)$

由公式(5)有：

$\lambda v_{i}=\frac{1}{n}\sum_{t=1}^{n}x(t)x(t)^{T}v_{i}=\frac{1}{n}\sum_{t=1}^{n}(x(t)\cdot v_{i})x(t)...............................(9)$

如果假定 $v_{i}$ 的模长为 $\lambda$ ，两边同时除以 $v_{i}$ 的模长有：

$v_{i}=\frac{1}{n}\sum_{t=1}^{n}x(t)x(t)^{T}v_{i}=\frac{1}{n}\sum_{t=1}^{n}(\frac{x(t)\cdot v_{i}}{||v_{i}||})x(t)..........................(10)$

从统计学的有效性角度来讲，对于同一个观测量集合而言，评估误差越小，评估值越有效。一般情况下，对于很多分布（高斯分布，指数分布）而言，最大似然估计的均值为样本的均值，而当评估值等于均值时，对应MLE最大，因此 $v_{i}$ 取评估值得均值，可以达到统计学意义上的有效。

式(10)对应于增量式评估的过程，但是这是一个batch处理版本，其对应的增量式版本为：

$v(t)=\frac{t-1}{t}v(t-1)+\frac{1}{t}u(t).......................................(11)$

式(11)表明，为了得到当前时刻评估最优，我们要同时设置学习率1/t，及残差率(t-1)/t，学习率 1/t保障了最优的"step size"，这也即是LCA的第二个最优——步长大小最优。

4、LCA算法流程

1、序列初始化：使用前C个输入样本数据，初始化C个cells，并初始化cell的更新年龄为1

$v_{i}(0)=x_{i},i=1,2,...,C$

$n_{i}=1,i=1,2,...,C$

2、学习和更新： $j=C+1,C+2,...$

1) 计算神经元响应：

$y_{i}=\frac{x(t)v_{i}(t-1)}{||v_{i}(t-1))||},i=1,2,...,C$

其中， $x(t)$ 表示第t个时刻对应样本，对应于第j个样本。

2) 不同特征之间侧抑制和稀疏编码：

按照神经元响应的大小顺序，选取前top-k个神经元进行激活，采用这种非迭代的排序机制替换掉了重复的迭代过程，进而保证了计算的有效性。然后使用线性函数对响应进行缩放，保证响应在0，1之间：

${y}'_{i}=(y_{i}-y_{k+1})/(y_{1}-y_{k+1})$

3) 最优Hebbian学习：

使用时间可塑性设计，更新竞争优胜的前top-k个神经元

$v_{j}(t)=\omega _{1}v(t-1)+\omega _{2}y_{j}x(t)$

$\omega _{1}$ 对应残差率， $\omega _{2}$ 对应于学习率：

$\omega _{1}=\frac{n_{j}-1-\mu (n_{j})}{n_{j}},\omega _{2}=\frac{1+\mu (n_{j})}{n_{j}}$

$\mu (n_{j})$ 对应于遗忘函数。

4) 侧兴奋：这个对应于MILN中 Topographic这个概念

5) 长短期记忆：只更新优胜的top-k个神经元，其余的神经元即对应于长期记忆，更新的top-k个神经元对应于短期记忆。

这里可以看到，CCIPCA与CCILCA最大的不同之处在于，CCIPCA目的在于提取样本集数据对应最判别的前K个特征，实现对数据的降维，CCILCA目的在于寻找样本集中中C个样本分布密度最大的方向（相当于方向上的聚类），对应C个叶区域，进而将样本与样本进行区分。同时在更新步骤中，当输入一个样本时，CCIPCA使用这个样本数据对所有的判别特征进行更新，CCILCA则只对与当前样本最匹配的前top-k个特征向量进行更新。

未完待续~~~~~~~

参考文献：

Bell A J, Sejnowski T J. The "independent components" of natural scenes are edge filters.[J]. Vision Research, 1997, 37(23):3327-38.

Weng J, Luciw M. Dually Optimal Neuronal Layers: Lobe Component Analysis[J]. IEEE Transactions on Autonomous Mental Development, 2009, 1(1):68-85.

LCA（Lobe Component Analysis）：叶成分分析

猜你喜欢