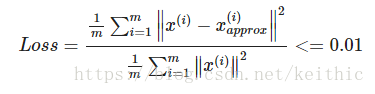主成分分析（降维）

数据量太大时往往会有相关性较高的维度，给建模计算带来不必要的开支。

算法步骤：

输入：n维样本集 $D=(x^{(1)}, x^{(2)},...,x^{(m)})$ ，要降维到的维数n'.

　　　　输出：降维后的样本集D'

　　　　1) 对所有的样本进行中心化： $x^{(i)} = x^{(i)} - \frac{1}{m}\sum\limits_{j=1}^{m} x^{(j)}$

　　　　2) 计算样本的协方差矩阵 $XX^T$

　　　　3) 对矩阵 $XX^T$ 进行特征值分解

　　　　4）取出最大的n'个特征值对应的特征向量 $(w_1,w_2,...,w_{n'}),$ 将所有的特征向量标准化后，组成特征向量矩阵W。

　　　　5）对样本集中的每一个样本 $x^{(i)}$ ,转化为新的样本 $z^{(i)}=W^Tx^{(i)}$

　　　　6) 得到输出样本集 $D' =(z^{(1)}, z^{(2)},...,z^{(m)})$

推导：

PCA思想：

将高维数据投影至低维空间，从而减少获得源数据的主要特征。
获得低维转换的方法：在低维空间里方差最大。

有mXn维数据 $(x^{(1)}, x^{(2)},...,x^{(m)})$ ，对其去中心化， $\sum\limits_{i=1}^{m}x^{(i)}=0$ 。设新坐标系正交基为 $\{w_1,w_2,...,w_n\},$ $||w||_2=1, w_i^Tw_j=0$ 。

则有新坐标系的样本 $W^TX$ ，样本点 $x^{(i)}$ 在n'维坐标系中的投影为： $z^{(i)} = (z_1^{(i)}, z_2^{(i)},...,z_{n'}^{(i)})$ .其中， $z_j^{(i)} = w_j^Tx^{(i)}$ 。在新坐标系中的投影方差为 $W^Tx^{(i)}x^{(i)T}W$ 。

要使所有的样本的投影方差和最大，也就是最大化 $\sum\limits_{i=1}^{m}W^Tx^{(i)}x^{(i)T}W,$ 即：

$\underbrace{arg\;max}_{W}\;tr( W^TXX^TW) \;\;s.t. W^TW=I$

利用拉格朗日函数可以得到

$J(W) = tr( W^TXX^TW) + \lambda(W^TW-I)$

对W求导有 $XX^TW+\lambda W=0$ , 整理下即为：

$XX^TW=\lambda W$

而上式即是一个方阵的特征分解公式： $A \nu = \lambda \nu$ ;

其中，XX^T是方阵，W是特征向量，\lambda 是特征值。

于是上面求解的问题转化为求协方差矩阵的特征值和特征向量。（特征向量即是新坐标系正交基，特征值指示的是变化程度，特征值大表示变换后离散程度高，方差大）因此，获取特征值和特征向量后，取特征值按大小排列取n'个，其对应的特征向量组成矩阵W，于是新坐标 $z^{(i)}=W^Tx^{(i)}。$ 。

n'的选取（要能最大化代表原样本）

$\frac{\sum\limits_{i=1}^{n'}\lambda_i}{\sum\limits_{i=1}^{n}\lambda_i} \geq t$ t为阈值。

也即：

分子表示：平均投影误差的平方（Average squared projection error）, 其实就是原始值和重构值之间差的平方的平均值。分母表示：原始数据的总变差（Total varia1on in the data）这个公式所表达的意思就是：99% 的差异性被保留了。

奇异值分解(SVD)的计算方法

奇异值分解是线性代数中一种重要的矩阵分解方法，这篇文章通过一个具体的例子来说明如何对一个矩阵A进行奇异值分解。

首先，对于一个m*n的矩阵，如果存在正交矩阵 $U(m*m) V(n*n)$ ，使得(1)式成立：

$A=U \Sigma V^T \tag{1}$

则将式(1)的过程称为奇异值分解，其中 $\Sigma_{mn}=\begin{bmatrix}\Sigma_1 & 0 \\ 0 & 0\end{bmatrix}$ ，且 $\Sigma_1=diag(\sigma_1,\sigma_1,\dots,\sigma_r)$ ,U和V分别称为A的左奇异向量矩阵和右奇异向量矩阵。下面用一个具体的例子来说明如何得到上述的分解。假设我们有一个矩阵 $A=\begin{bmatrix} 1&1\\1&1\\0&0\end{bmatrix}$

第一步计算U，计算矩阵 $AA^T=\begin{bmatrix} 2&2&0\\2&2&0\\0&0&0\end{bmatrix}$ ,对其进行特征分解，分别得到特征值4,0,0和对应的特征向量 $[\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}},0]^T,[-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}},0]^T,[0,0,1]^T$ ,可以得到 $U=\begin{bmatrix} \frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}&0 \\ \frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}&0 \\ 0&0&1 \end{bmatrix}$

第二步计算V，计算矩阵 $A^TA=\begin{bmatrix} 2&2 \\ 2&2 \end{bmatrix}$ ，对其进行特征分解，分别得到特征值4,0和对应的特征向量 $[\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}]^T,[-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}]^T$ ,可以得到 $V=\begin{bmatrix} \frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\end{bmatrix}$

第三步计算 $\Sigma_{mn}=\begin{bmatrix}\Sigma_1 & 0 \\ 0 & 0\end{bmatrix}$ ，其中 $\Sigma_1=diag(\sigma_1,\sigma_1,\dots,\sigma_r)$ 是将第一或第二步求出的非零特征值从大到小排列后开根号的值，这里 $\Sigma=\begin{bmatrix} 2&0 \\ 0&0 \\ 0&0 \end{bmatrix}$

最终，我们可以得到A的奇异值分解

$A=U \Sigma V^T= \begin{bmatrix} \frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}&0 \\ \frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}&0 \\ 0&0&1 \end{bmatrix} \begin{bmatrix} 2&0 \\ 0&0 \\ 0&0 \end{bmatrix} {\begin{bmatrix} \frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\end{bmatrix}}^T=\begin{bmatrix} 1&1\\1&1\\0&0\end{bmatrix}$

矩阵的特征值分解和奇异值分解有什么区别？

首先，特征值只能作用在一个m*m的正方矩阵上，而奇异值分解则可以作用在一个m*n的长方矩阵上。其次，奇异值分解同时包含了旋转、缩放和投影三种作用，(1)式中，U和V都起到了对A旋转的作用，而\Sigma起到了对A缩放的作用。特征值分解只有缩放的效果。

http://blog.codinglabs.org/articles/pca-tutorial.html

http://www.fanyeong.com/2017/07/11/machine-learning-clustering-dimensionality-reduction/

http://www.cnblogs.com/pinard/p/6239403.html

https://byjiang.com/2017/11/18/SVD/

主成分分析（降维）

猜你喜欢