理解降维算法之PCA(主成分分析）

PCA算法流程

输入：n维样本集D=(x(1),x(2),…,x(m))，要降维到的维数n’.

输出：降维后的样本集D′
1)对所有的样本进行中心化：

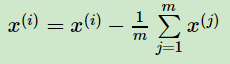
2) 计算样本的协方差矩阵 $X{X^T}$
3) 对矩阵 $X{X^T}$ 进行特征值分解(即求解特征值和特征向量）

4)取出最大的n’个特征值对应的特征向量(w1,w2,…,wn′), 将所有的特征向量标准化后，组成特征向量矩阵W。
5)对样本集中的每一个样本x(i),转化为新的样本z(i)= ${W^T}x(i)$
6) 得到输出样本集D′=(z(1),z(2),…,z(m))
　 有时候，我们不指定降维后的n’的值，而是换种方式，指定一个降维到的主成分比重阈值t。这个阈值t在（0,1]之间。假如我们的n个特征值为λ1≥λ2≥…≥λn,则n’可以通过下式得到:

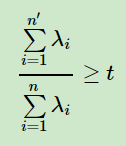
PCA理解实例

下面举一个简单的例子，说明PCA的过程。
假设我们的数据集有10个二维数据(2.5,2.4), (0.5,0.7), (2.2,2.9), (1.9,2.2), (3.1,3.0), (2.3, 2.7), (2, 1.6), (1, 1.1), (1.5, 1.6), (1.1, 0.9)，需要用PCA降到1维特征。
首先我们对样本中心化，这里样本的均值为(1.81, 1.91),所有的样本减去这个均值后，即中心化后的数据集为(0.69, 0.49), (-1.31, -1.21), (0.39, 0.99), (0.09, 0.29), (1.29, 1.09), (0.49, 0.79), (0.19, -0.31), (-0.81, -0.81), (-0.31, -0.31), (-0.71, -1.01)。
现在我们开始求样本的协方差矩阵，由于我们是二维的，则协方差矩阵为：

$X{X^T}$=(cov(x1,x1)cov(x2,x1)
cov(x1,x2)cov(x2,x2))
对于我们的数据，求出协方差矩阵为：

$X{X^T}$=(0.616555556 0.615444444
0.6154444440.716555556)
求出特征值为（0.0490833989， 1.28402771），对应的特征向量分别为：(0.735178656,0.677873399)T，(−0.677873399,−0.735178656)T,由于最大的k=1个特征值为1.28402771，对于的k=1个特征向量为(−0.677873399,−0.735178656)T. 则我们的W=(−0.677873399,−0.735178656)T
　　　　我们对所有的数据集进行投影z(i)= ${W^T}x(i)$，得到PCA降维后的10个一维数据集为：(-0.827970186， 1.77758033， -0.992197494， -0.274210416， -1.67580142， -0.912949103， 0.0991094375， 1.14457216, 0.438046137， 1.22382056)
注，公式推导部分没有总结，可以查看已有资料的推导

参考

刘建平老师博客