降维(一) 主成分分析（Principal Components Analysis）

为什么需要降维？

$\qquad$如果我们希望模型的精度比较高，或者说泛化误差率较小，那么我们希样本的采样密度足够大（密采样），即在任意样本 $x$附近任意小的 $\delta$距离范围内总能找到一个样本。

$\qquad$假设所有样本在其属性上归一化，对于 $\delta=0.001$，仅考虑单个属性，需要1000个样本点平均分布在其取值范围内，可以保证所有样本在其附近0.001范围内总能找到一个训练样本。但是，维数增大时，假定属性维数为20，若要满足密采样的要求，则至少需 $(10^3)^{20}=10^{60}$个样本。

$\qquad$事实上，在高维情形下出现的样本稀疏、距离计算困难等问题，是所有机器学习方法面临的严重障碍，被称为“维数灾难”。

缓解维数灾难的一个重要途径就是降维：

• 通过某种数学变换将原始高维属性空间转变为一个低维“子空间”，在这个子空间中样本密度大幅提高，距离计算也变得更为容易。

• 但是要保证原始空间中样本之间的距离在低维空间中得以保持，且在低维子空间中更容易学习。

常用的降维方法有两种：PCA、LDA。

这里先总结PCA的思想和过程：

主成分分析（PCA）

$\qquad$主成分分析（Principal components analysis，简称PCA）是最重要的降维方法之一，在数据压缩消除冗余和数据噪音消除等领域都有广泛的应用。

1、思想

$\qquad$PCA中主成分的意思就是找出数据里最主要的方面，用数据里最主要的方面来代替原始数据。具体的，假如我们的数据集是 $n$维的，共有 $m$个数据 $(x^{(1)},x^{(2)},...,x^{(m)})$。我们希望将这 $m$个数据的维度从 $n$维降到 $n'$维，希望这 $m$个 $n'$维的数据集尽可能的代表原始数据集。我们知道数据从 $n$维降到 $n'$维肯定会有损失，但是我们希望损失尽可能的小。那么如何让这 $n'$维的数据尽可能表示原来的数据呢？

$\qquad$我们先看看最简单的情况，也就是n=2，n’=1，也就是将数据从二维降维到一维。数据如下图。我们希望找到某一个维度方向，它可以代表这两个维度的数据。图中列了两个向量方向，u1和u2，那么哪个向量可以更好的代表原始数据集呢？从直观上也可以看出，u1比u2好。

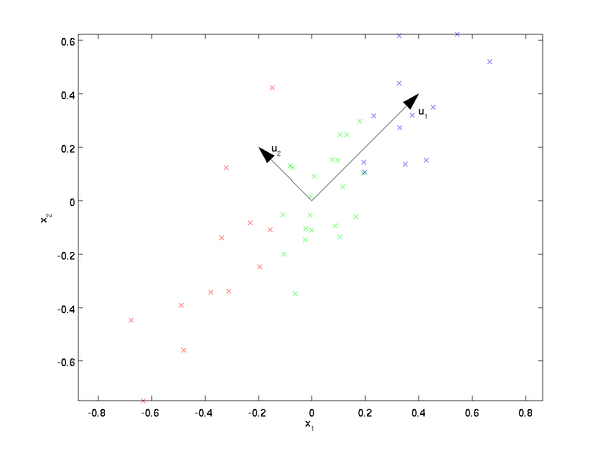
$\qquad$为什么u1比u2好呢？可以有两种解释，第一种解释是样本点到这个直线的距离足够近，第二种解释是样本点在这个直线上的投影能尽可能的分开。

$\qquad$假如我们把n’从1维推广到任意维，则我们的希望降维的标准为：

• 样本点到这个超平面的距离足够近；
• 样本点在这个超平面上的投影能尽可能的分开(方差最大)。

---

2、原理

通过上面的分析可以从两方面推导出如下结果：
$\underbrace{arg\;min}_{W}\;-tr( W^TXX^TW) \;\;s.t. W^TW=I$
或者：
$\underbrace{arg\;max}_{W}\;tr( W^TXX^TW) \;\;s.t. W^TW=I$
因此将问题转化为有约束的最优化问题，于是可以采用拉格朗日乘数法，得到：
$J(W) = -tr( W^TXX^TW + \lambda(W^TW-I))$
对 $W$求导有 $−XX^TW+λW=0$，得到：
$XX^TW=\lambda W$
即：
$W^TXX^TW=\lambda W^TW=\lambda$

$\qquad$由上式可以知道当 $\lambda$取最大值时可以使 $W^TXX^TW$达到最大值。

$\qquad$因此，当我们将数据集从 $n$维降到 $n'$维时，需要找到最大的 $n'$个特征值对应的特征向量。这 $n'$个特征向量组成的矩阵 $W$即为我们需要的矩阵。对于原始数据集，我们只需要用 $z^{(i)}=W^Tx^{(i)}$，就可以把原始数据集降维到最小投影距离或最大方差的 $n'$维数据集。

---

3、过程

$\qquad$求样本 $x^{(i)}$的 $n'$维的主成分其实就是求样本集的协方差矩阵 $XX^T$的前 $n'$个特征值对应特征向量矩阵 $W$，然后对于每个样本 $x^{(i)}$，做如下变换 $z^{(i)}=W^Tx^{(i)}$，即达到降维的目的。

具体的算法流程：

输入： $n$维样本集 $D=(x^{(1)}, x^{(2)},...,x^{(m)})$，要降维到的维数 $n'$。
输出：降维后的样本集 $D′$
（1）对所有的样本进行中心化： $x^{(i)} = x^{(i)} - \frac{1}{m}\sum\limits_{j=1}^{m} x^{(j)}$;
（2）计算样本的协方差矩阵 $XX^T$;
（3）对矩阵 $XX^T$进行特征值分解;
（4）取出最大的 $n'$个特征值对应的特征向量 $(w_1,w_2,...,w_{n'})$, 将所有的特征向量标准化后，组成特征向量矩阵 $W$;
（5）对样本集中的每一个样本 $x^{(i)}$,转化为新的样本 $z^{(i)}=W^Tx^{(i)}$;
（6）得到输出样本集 $D' =(z^{(1)}, z^{(2)},...,z^{(m)})$。

$\qquad$有时候，我们不指定降维后的 $n'$的值，而是换种方式，指定一个降维到的主成分比重阈值 $t$。这个阈值 $t$在 $(0,1]$之间。假如我们的 $n$个特征值为 $\lambda_1 \geq \lambda_2 \geq ... \geq \lambda_n$，则 $n'$可以通过下式得到：
$\frac{\sum\limits_{i=1}^{n'}\lambda_i}{\sum\limits_{i=1}^{n}\lambda_i} \geq t$
$\qquad$这里的阈值t的另一种理解：保留矩阵中的能量信息。如果t=95%，意味着取最大的 $n'$个特征值使其保留原始矩阵中的95%以上的能量信息，具体保留能量信息的多少根据需要而定。

---

4、实例

$\qquad$下面举一个简单的例子，说明PCA的过程。

$\qquad$假设我们的数据集有10个二维数据 $(2.5,2.4), (0.5,0.7), (2.2,2.9), (1.9,2.2), (3.1,3.0), (2.3, 2.7), (2, 1.6), (1, 1.1), (1.5, 1.6), (1.1, 0.9)$，需要用PCA降到1维特征。

$\qquad$首先我们对样本中心化，这里样本的均值为 $(1.81, 1.91)$，所有的样本减去这个均值后，即中心化后的数据集为(0.69, 0.49), (-1.31, -1.21), (0.39, 0.99), (0.09, 0.29), (1.29, 1.09), (0.49, 0.79), (0.19, -0.31), (-0.81, -0.81), (-0.31, -0.31), (-0.71, -1.01)。

$\qquad$现在我们开始求样本的协方差矩阵，由于我们是二维的，则协方差矩阵为：
$\mathbf{XX^T} = \left( \begin{array}{ccc} cov(x_1,x_1) & cov(x_1,x_2)\\ cov(x_2,x_1) & cov(x_2,x_2) \end{array} \right)$
对于我们的数据，求出协方差矩阵为：
$\mathbf{XX^T} = \left( \begin{array}{ccc} 0.616555556 & 0.615444444\\ 0.615444444 & 0.716555556 \end{array} \right)$
求出特征值为 $(0.490833989, 1.28402771)$，对应的特征向量分别为： $(0.735178656, 0.677873399)^T、(−0.677873399, −0.735178656)^T$，由于最大的k=1个特征值为 $1.28402771$，对于的k=1个特征向量为 $(−0.677873399, −0.735178656)^T$。则我们的 $W=(−0.677873399, −0.735178656)^T$
　　我们对所有的数据集进行投影 $z^{(i)}=W^Tx^{(i)}$，得到PCA降维后的10个一维数据集为：(-0.827970186, 1.77758033, -0.992197494, -0.274210416, -1.67580142, -0.912949103, 0.0991094375, 1.14457216, 0.438046137, 1.22382056)

---

5、简单实现

下面是实例中的二维数据降维的简单实现：

import matplotlib.pyplot as plt
import numpy as np

class PCA:
    def pca(self, X, n):
        """
        PCA
        :param X: 输入数据
        :param n: 保留维度
        :return: z: 降维后数据  recon_mat: 重构数据
        """
        # 中心化
        X_avg = np.average(X, axis=0)
        X_core = X - X_avg
        # 协方差矩阵
        X_cov = np.cov(X_core.T)
        # 取最大的n个特征值和特征向量
        eig_value, eig_vec = np.linalg.eig(np.mat(X_cov))
        eig_value_sort = np.argsort(eig_value)
        eig_max_index = eig_value_sort[-1:-(n + 1):-1]
        # 特征向量矩阵W
        W = eig_vec[:, eig_max_index]
        z = X_core * W
        # 重构数据
        recon_mat = z * W.T + X_avg
        return z, recon_mat

    def pca_pencent(self, X, percentage):
        """
        PCA：利用能量信息进行降维

        :param X: 输入数据
        :param percentage: 保留能量信息百分比
        :return: z: 降维后数据  recon_mat: 重构数据
        """
        # 中心化
        X_avg = np.average(X, axis=0)
        X_core = X - X_avg
        # 协方差矩阵
        X_cov = np.cov(X_core.T)
        # 求特征值和特征向量
        eig_value, eig_vec = np.linalg.eig(np.mat(X_cov))
        # 求主成分个数
        n = self.percent_n(eig_value, percentage)
        eig_value_sort = np.argsort(eig_value)
        eig_max_index = eig_value_sort[-1:-(n + 1):-1]
        # 特征向量矩阵W
        W = eig_vec[:, eig_max_index]
        z = X_core * W
        # 重构数据
        recon_mat = z * W.T + X_avg
        return z, recon_mat

    def percent_n(self, eig_value, percentage):
        """
        求主成分个数

        :param eig_value: 特征值
        :param percentage: 保留能量信息百分比
        :return: 主成分个数
        """
        # 特征值排序：从大到小
        sort_eig_val = np.sort(eig_value)
        sort_eig_val = sort_eig_val[-1::-1]
        # 保留要求的能量信息，求主成分个数
        eig_sum = sum(sort_eig_val)
        tmp_sum = 0.0
        num = 0
        for eig in sort_eig_val:
            tmp_sum += eig
            num += 1
            if tmp_sum >= eig_sum * percentage:
                return num


if __name__ == '__main__':
    # 输入数据
    raw_data = [[2.5, 2.4], [0.5, 0.7], [2.2, 2.9], [1.9, 2.2], [3.1, 3.0], [2.3, 2.7], [2, 1.6], [1, 1.1], [1.5, 1.6], [1.1, 0.9]]
    data = np.array(raw_data)

    PCA = PCA()
    
    # 降维(指定维度)
    z, recon_data = PCA.pca(data, 1)
    print("降维后数据：\n", z)
    print("降维后重构数据：\n", recon_data)

    # 降维(给出保留的能量信息百分比)
    z, recon_data = PCA.pca_pencent(data, 0.95)
    print("降维后数据：\n", z)
    print("降维后重构数据：\n", recon_data)

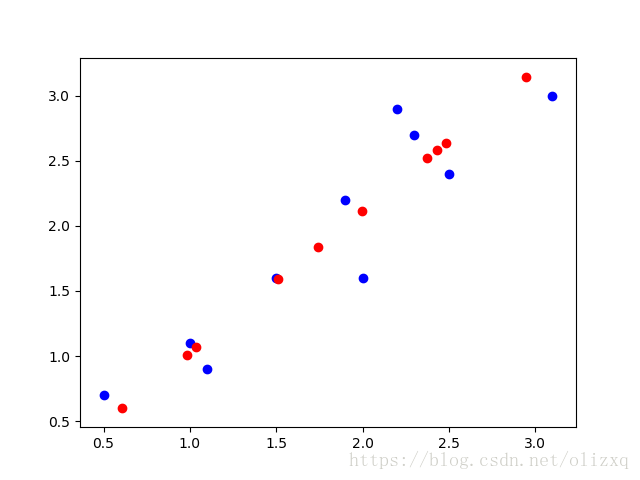
    # 降维前后数据对比
    recon_data = np.array(recon_data.tolist())
    plt.scatter(data[:, 0], data[:, 1], c='b')
    plt.scatter(recon_data[:, 0], recon_data[:, 1], c='r')
    plt.show()

运行结果：

降维后数据：
 [[-0.82797019]
 [ 1.77758033]
 [-0.99219749]
 [-0.27421042]
 [-1.67580142]
 [-0.9129491 ]
 [ 0.09910944]
 [ 1.14457216]
 [ 0.43804614]
 [ 1.22382056]]
降维后重构数据：
 [[2.37125896 2.51870601]
 [0.60502558 0.60316089]
 [2.48258429 2.63944242]
 [1.99587995 2.11159364]
 [2.9459812  3.14201343]
 [2.42886391 2.58118069]
 [1.74281635 1.83713686]
 [1.03412498 1.06853498]
 [1.51306018 1.58795783]
 [0.9804046  1.01027325]]

其中，蓝色点为原始数据，红色点为降维后重构的数据。

利用降维后保留的能量百分比确定主成分个数的算法，当t=0.95是结果与上面相同；当t=0.99时，保持原始维度，不会进行降维。

---

6、非线性降维——核主成分分析KPCA

$\qquad$在上面的PCA算法中，我们假设存在一个线性的超平面，可以让我们对数据进行投影。但是有些时候，数据不是线性的，不能直接进行PCA降维。

$\qquad$这里就需要用到和支持向量机一样的核函数的思想，先把数据集从 $n$维映射到线性可分的高维 $N>n$,然后再从 $N$维降维到一个低维度 $n'$，这里的维度之间满足 $n'<n<N$。

$\qquad$使用了核函数的主成分分析一般称之为核主成分分析（Kernelized PCA, 以下简称KPCA）。假设高维空间的数据是由n维空间的数据通过映射 $ϕ$产生。

$\qquad$则对于n维空间的特征分解：
$\sum\limits_{i=1}^{m}x^{(i)}x^{(i)T}W=\lambda W$
$\qquad$映射为：
$\sum\limits_{i=1}^{m}\phi(x^{(i)})\phi(x^{(i)})^TW=\lambda W$
通过在高维空间进行协方差矩阵的特征值分解，然后用和PCA一样的方法进行降维。一般来说，映射 $ϕ$不用显式的计算，而是在需要计算的时候通过核函数完成。由于KPCA需要核函数的运算，因此它的计算量要比PCA大很多。

---

7、总结

作为一个非监督学习的降维方法，它只需要特征值分解，就可以对数据进行压缩，去噪。因此在实际场景应用很广泛。为了克服PCA的一些缺点，出现了很多PCA的变种，比如第6部分为解决非线性降维的KPCA，还有解决内存限制的增量PCA方法Incremental PCA，以及解决稀疏数据降维的PCA方法Sparse PCA等。

PCA算法的主要优点有：

• 仅仅需要以方差衡量信息量，不受数据集以外的因素影响。

• 各主成分之间正交，可消除原始数据成分间的相互影响的因素。

• 计算方法简单，主要运算是特征值分解，易于实现。

PCA算法的主要缺点有：

• 主成分各个特征维度的含义具有一定的模糊性，不如原始样本特征的解释性强。
• 方差小的非主成分也可能含有对样本差异的重要信息，因降维丢弃可能对后续数据处理有影响。

参考：
http://www.cnblogs.com/pinard/p/6239403.html
《机器学习实战》