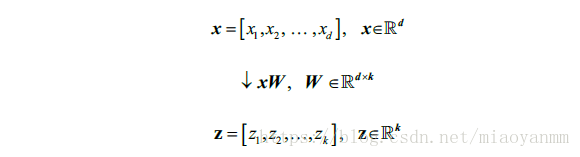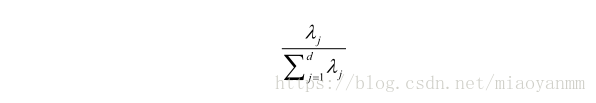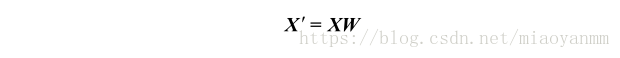数据压缩技术可以帮助我们对数据进行存储和分析,特征提取通过归纳总结数据集所蕴含的信息,可以将原始数据集变换到一个维度更低的新的特征子空间,从而实现数据压缩。
无监督数据降维技术——主成分分析
主成分分析是一种广泛应用于不同领域的无监督线性数据转换技术,其突出作用是降维。
PCA的目标是在高维数据中找到最大方差的方向,并将数据映射到一个维度不大于原始数据的新的子空间上。
如果使用PCA降维,我们将构建一个 d * k维的转换矩阵 W,这样可以将一个样本向量 x 映射到一个新的 k 维特征子空间上去,此空间的维度小于原始的 d 的维特征空间:
完成从原始 d 维数据到新的 k 维子空间,第一主成分的方差应该是最大的,由于各主成分之间是不相关的(正交的),后续主成分也具备尽可能大的方差。需要注意的是,主成分的方向对数据值的范围高度敏感,因此,需要先对特征进行标准化处理,以让各特征具有相同的重要性。
import pandas as pd
df_wine = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data', header=None)
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
sc = StandardScaler()
X_train_std = sc.fit_transform(X_train)
X_test_std = sc.transform(X_test)通过上述代码完成数据的预处理后,进入第二步:构造协方差矩阵。可通过如下公式计算两个特征
和
之间的协方差:
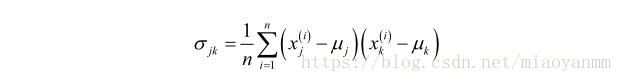
和
分别为特征 j 和 k 的均值。请注意,如果对数据集做了标准化处理,样本的均值将为0。
协方差矩阵的特征向量代表主成分(最大方差方向),而对应的特征值大小就决定了特征向量的重要性。
numpy中的linalg.eig函数可以用来计算数据集协方差矩阵的特征对。
import numpy as np
cov_mat = np.cov(X_train_std.T)
eigen_vals, eigen_vecs = np.linalg.eig(cov_mat)
print('\nEigenvalues \n%s' % eigen_vals)执行结果如下:
Eigenvalues
[4.8923083 2.46635032 1.42809973 1.01233462 0.84906459 0.60181514
0.52251546 0.08414846 0.33051429 0.29595018 0.16831254 0.21432212
0.2399553 ]因为要将数据集压缩到一个新的特征子空间上来实现数据降维,所以只选择那些包含最多信息(方差最大)的特征向量(主成分)组成子集。由于特征值的大小决定了特征向量的重要性,因此需要将特征值按降序排列。在整理包含信息量最大的前 k 个特征向量前,先绘制特征值的方差贡献率(variance explained ratios)图像。
特征值
的方差贡献率是指,特征值
与所有特征值和的比值:
tot = sum(eigen_vals)
var_exp = [(i / tot) for i in sorted(eigen_vals, reverse=True)]
cum_var_exp = np.cumsum(var_exp)
import matplotlib.pyplot as plt
plt.bar(range(1, 14), var_exp, alpha=0.5, align='center', label='individual explained variance')
plt.step(range(1, 14), cum_var_exp, where='mid', label='cumulative explained variance')
plt.ylabel('Explained variance ration')
plt.xlabel('Principal components')
plt.legend(loc='best')
plt.show()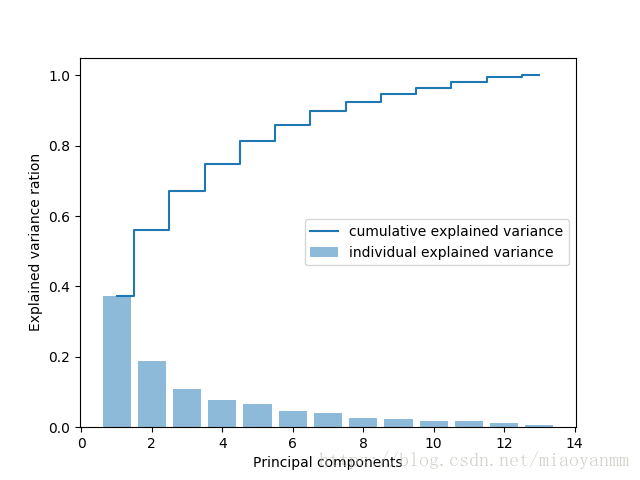
由图可以看到,第一主成分占方差总和的 40% 左右;此外,还可以看出前两个主成分占总体方差的近 60%。
特征转换
将协方差矩阵分解为特征对后,我们将对特征值按降序进行排列,并通过挑选出对应的特征向量构造出映射矩阵,然后使用映射矩阵将数据转换到低维的子空间上。
eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:, i]) for i in range(len(eigen_vals))]
eigen_pairs.sort(reverse=True)
W = np.hstack((eigen_pairs[0][1][:, np.newaxis], eigen_pairs[1][1][:, np.newaxis]))
print('Matrix W:\n', W)Matrix W:
[[ 0.14669811 0.50417079]
[-0.24224554 0.24216889]
[-0.02993442 0.28698484]
[-0.25519002 -0.06468718]
[ 0.12079772 0.22995385]
[ 0.38934455 0.09363991]
[ 0.42326486 0.01088622]
[-0.30634956 0.01870216]
[ 0.30572219 0.03040352]
[-0.09869191 0.54527081]
[ 0.30032535 -0.27924322]
[ 0.36821154 -0.174365 ]
[ 0.29259713 0.36315461]]本例只选择了两个特征向量,前两个特征值之和占据了数据集总体方差的60%。在实际应用中,确定主成分的数量时,需要根据实际情况在计算效率与分类器性能之间做出权衡。
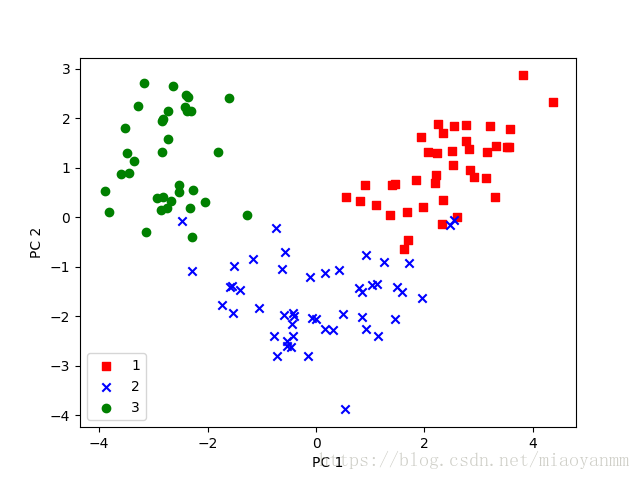
通过计算矩阵的点积,可以将整个 124 * 13 维的训练数据集转换到包含两个主成分的子空间上:
X_train_pca = X_train_std.dot(W)
colors = ['r', 'b', 'g']
markers = ['s', 'x', 'o']
for l, c, m in zip(np.unique(y_train), colors, markers):
plt.scatter(X_train_pca[y_train == l, 0], X_train_pca[y_train == l, 1], c=c, label=l, marker=m)
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc='lower left')
plt.show()使用scikit-learn进行主成分分析
PCA也是scikit-learn中的一个数据转换类。下面,我们使用scikit-learn中的PCA对葡萄酒数据集做预处理,然后使用逻辑回归对转换后的数据进行分类,最后定义 plot_decision_region 函数对决策区域进行可视化展示。
from matplotlib.colors import ListedColormap
def plot_decision_regions(X, y, classifier, resolution=0.02):
# setup marker generator and color map
markers = ('s', 'x', 'o', '^', 'v')
colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
cmap = ListedColormap(colors[: len(np.unique(y))])
#plot the decision surface
x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution), np.arange(x2_min, x2_max, resolution))
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
#plot class samples
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1], alpha=0.8, c=cmap(idx), marker=markers[idx], label=cl)
from sklearn.linear_model import LogisticRegression
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
lr = LogisticRegression()
X_train_pca = pca.fit_transform(X_train_std)
X_test_pca = pca.transform(X_test_std)
lr.fit(X_train_pca, y_train)
plot_decision_regions(X_test_pca, y_test, classifier=lr)
plt.ylabel('PC1')
plt.xlabel('PC2')
plt.legend(loc='lower left')
plt.show()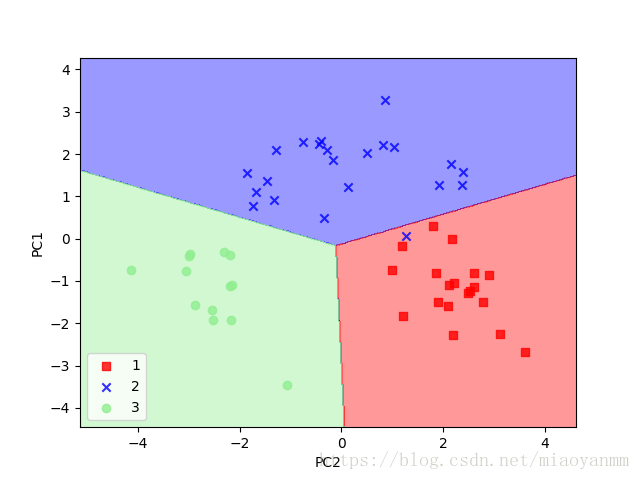
执行上述代码,绘制出了测试集的决策区域,可以看到:逻辑回归在这个小的二维特征子空间上表现优异,只误判了1个样本。
请注意,在初始化PCA类时,将 n_components 设置为None,那么它将按照方差贡献率递减顺序返回所有的主成分,而不是进行降维操作。
参考文献:
Python Machine Learning/Chapter 5: Compressing Data via Dimensionality Reduction