在数据挖掘过程中,当一个对象有多个属性(即该对象的测量过程产生多个变量)时,会产生高维度数据,这给数据挖掘工作带来了难度,我们希望用较少的变量来描述数据的绝大多数信息,此时一个比较好的方法是先对数据进行降维处理。数据降维过程不是简单提取部分变量进行分析,这样的方式法当然会降低数据维度,但是这是非常不可取的方式(不专业一点,可以称之为“丢维”),违背了“降维”的含义。
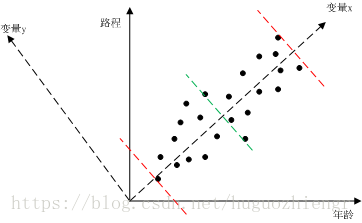
尽管我们并不确定不同变量之间是否一定有关系,但除非有确定的依据,我们最好还是猜测是有关系的,先看一个简单的例子,只有两个变量的情况。我们对人的年龄和他当前所走过的路程进行统计,然后绘制成图1(此处的例子是自己想的,不太妥当,只为说明问题)
图1
在图1中,我们对所有的样点进行一元线性回归分析,可以得到变量x直线,将变量x直线逆时针旋转90度,得到变量y直线(得到我们熟悉的二维直角坐标系),我们可以直观的看到样本数据主要沿着变量x分布,那么在数学上怎么去判别这种“直观的分布”呢?我们用最大方差来判别。图1中两条红色虚线是样本沿变量x的分布范围,绿色虚线是样本数据在变量x这一维度上的均值,这样我们就可以求得样本数据在变量x维度上的方差,类似的,可以求得样本数据在变量y上的方差,很明显,样本数据在变量x维度上的方差较大。
那么方差大说明什么问题呢?方差大说明样本数据在该维度上包含更多的信息。我们可以这样想,如果样本数据在某个维度上基本不变化,那么说明这个维度代表的变量的有、无对数据分布没有影响,该变量就没有存在的必要了,在测量过程中,我们就不必测量对象的这个属性。所以,此时可以用变量x这样一个变量来描述对象的年龄、路程属性。
这里还有两个问题需要说明,一个是变量x代表什么含义,另外一个就是在多维数据降维过程中,什么样的变量(类似于变量x这种)才是符合我们要求的变量。在我码这些字的时候,我也没弄明白问题一,所以先跳过,后面弄明白了再来补充。对于问题二,在降维之后,我们会得到一系列的新的维度,以及这些维度所代表的变量,按照样本数据在这些维度上的投影所得数据的方差大小,对这些新的变量进行排列。假设我们选择前n个新的变量(假设有的话),这n个新的变量就已经包含了原数据信息的90%,而这个比例也是我们能够接受的,那么这前n个变量就是满足我们需求的。
下面仔细说明降维的过程(为了方便,所有的向量这里我就不加方向箭头,只是标黑处理)
1. 假设X是一个 的数据矩阵,行代表实例对象,列代表变量,我们先对每一列数据都去均值化,也即是列中数据都减去该列数据的均值(如果数据矩阵之前没有做过该处理)。我们关心的实际上是数据的变化情况,数据矩阵中每一个变量中的数值只是对变量的一种表示,表示的是具有变量所表示属性的不同实例对象间的相互关系(事实上我们可以对表示变量的数值做一系列变换,只要保持该变量的特性不变即可,例如大小、相等、加法、减法等),因此去均值后我们可以抛开测量过程带来的一些影响。
2. 假设向量a是当X沿其投影时会使方差最大化的 列向量(也即时降维后满足我们要求的变量多表示的维),现在将数据矩阵X向向量a上投影,得到Xa,这是一个
的投影值列向量,我们对投影值列向量的方差
定义为
(1)
由于X的均值为0, V即为数据矩阵X的协方差矩阵。
3. 在式(1)中,为了使得方差最大,我们可以对a各元素等比例放大,但是这是没有什么意义的,因此我们给a施加一个约束条件 —— a为单位向量,即
,通过引入拉格朗日乘子法,我们得到下列最优化问题方程
对a进行求导,得到
这样就得到我们熟悉的特征值形式
(2)
4. 通过公式(2)我们可以求得一系列特征值 及其对应的特征向量
,最大特征值对应的特征向量即为第一主成分分量,第二大特征值对应的特征向量即为第二主成分分量,以此类推。得到公式(2)后我们再回头看公式(1),方差
即为
,因此当我们选取前 k 个主成分分量来近似数据矩阵X时,可以对接近误差做如下定义
我们根据需要选取前k个主成分分量,并且使得接近误差在我们允许的范围内。