数据降维(三)PCA主成分分析

PCA主成分分析

目标函数1:最小化重建误差

重建误差是指将低维表示重新转化为高维表示时与原来的高维表示的误差.

最小化重建误差可用最小化所有样本的平方重建误差之和来替代.

• 假定 $||w_i||=1,w_i^Tw_j = 0(i\neq j)$为新坐标
• $w$用在两个函数上：
  • 编码： $z_i = W^Tx_i,z_{ij} = w_j^Tx_i$
  • 解码： $\tilde{x}_i = Wz_i = \sum_{j=1}^{d'}z_{ij}w_j$
• 目标：最小平方重建误差和 $min_{W\in R^{d\times d'}}\sum_{i=1}^m||x_i - Wz_i||^2$

重建误差： $||x-\tilde{x}||$

当低维恰好是高维在低维向量 $w_i$上的投影时，重构误差最小.

推导：
$\begin{aligned} \sum_{i=1}^m||x_i - Wz_i||^2 & = \sum_{i=1}^m||x_i - \sum_{j=1}^{d'}z_{ij}w_j||^2\\ & = \sum_{i=1}^mz_i^Tz_i - 2\sum_{j=1}^mz_i^TW^Tx_i + const\\ &\propto -tr(W^T(\sum_{i=1}^mx_ix_i^T)W)\\ & = - tr(W^TXX^TW) \end{aligned}$
其中，
$||w_i|| = 1, w_i^Tw_j = 0(i\neq j)$
$z_i = (z_{i1},z_{i2},\cdots,z_{id'})$
$z_i = W^Tx_i$
$z_{ij} = w_j^Tx_i是x_i在低维坐标系下第j维坐标$
$\tilde{x_i} = \sum_{j=1}^{d'}z_{ijw_j}是基于z_i重构得到的向量$

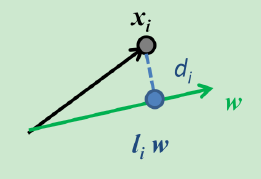
最小化重建误差即最小化 $d_i$，在给定样本 $x_i$的情况下，也就等价于最大化样本点在特征向量上的投影.

在数据归一化后(向量原点在样本均值上)，为了最大化样本点在特征向量上的投影，很容易发现特征向量应当沿着样本点分布范围最大的方向，即方差最大方向.

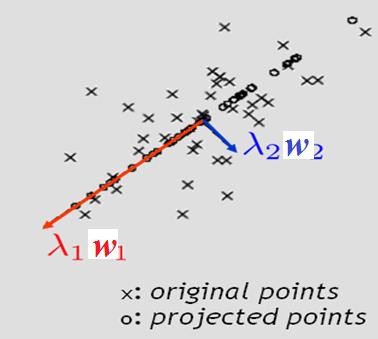
目标函数2：最大化方差

• 中心思想：寻找一个方向向量，使得数据投影到其上之后方差最大.
• 如果能找到就继续寻找下一个方向向量，该向量正交于之前的方向向量，并且尽可能保持数据方差.
• 这样的一些方向向量，称为主成分
• 目标是捕捉数据的内在变化
• 最大化样本投影的方差(假定样本中心化了)
  $\max\sum_iz_i^Tz_i = \max_w tr(W^TXX^TW)$

PCA目标函数计算

• 寻找 $W\in R^{d\times d'}$使得：
  $\max_W tr(W^TXX^TW)$
  $s.t.\ W^TW = 1$
• 拉格朗日(Lagrange)方法
  • 引入拉格朗日因子 $\lambda_i,1\leq i\leq d$得到拉格朗日方程：
    $L = Tr(W^TXX^TW) -\sum_{i=1}^d\lambda_i(w_i^Tw_i - 1)$
  • 矩阵的迹的性质
    $\frac{\partial tr(WAW^T)}{\partial W} = 2WA, A=A^T$
  • 令 $\frac{\partial L}{\partial W^T} = 0$，那么 $XX^TW = \lambda W$
  • $W$是 $XX^T$的特征向量

求解PCA(1)

输入： $X = {x_1,x_2\dots x_m}$，低维空间维度 $d'$
算法过程：

• $x_i = x_i - \frac{1}{m}\sum_{j=1}{m}x_j$
• 计算 $XX^T$
• 对 $XX^T$做特征分解
• $d'$最大特征值对应的特征向量 $w_1, w_2\dots w_{d'}$

输出： $W = (w_1, w_2\dots w_{d'})$

表现

原始维度不是非常大时表现良好.

如果原始维度很大，则可以采用奇异值分解(Singular Value Decomposition, SVD).

• 有一些实现可以直接找到最大的N个特征值对应的特征向量.

下面我们从SVD角度来考虑PCA.

• 奇异值是特征值的非负平方根
• $X_TX$的特征向量构成 $V^T$
• $XX^T$的特征向量构成 $U$
• $XX^T$和 $X^TX$具有相同的非零特征值

求解PCA(2)

输入： $X = {x_1,x_2\dots x_m}$，低维空间维度 $d'$
算法过程：

• $x_i = x_i - \frac{1}{m}\sum_{j=1}{m}x_j$
• 奇异值分解： $X\approx U_{d\times d} \sum_{d\times m}V_{m\times m}^T$
• $d'$奇异值对应的左奇异向量 $u_1, u_2\dots u_{d'}$

输出： $U = (u_1, u_2\dots u_{d'})$

参数d’

• 用户指定
• 利用简单的分类器(如KNN)通过交叉验证方式选择
• 使用重建阈值 $\frac{\sum_{i=1}^{d'}\lambda_i}{\sum_{j=1}^d\lambda_j}\geq t$(如方差的85%)

PCA总结

优点：

• 特征向量方法
• 没有额外要调节的参数
• 没有迭代
• 没有局部最小值

缺点：

• 只用了二阶统计量，不能处理高阶依赖
• 受限于线性投影