Expectation Maximization(EM)算法

概率模型有时既含有观测变量（observable variable），又含有隐变量（latent variable）。如果概率模型的变量都是观测变量，那么给定数据，可以直接用极大似然估计或贝叶斯估计来计算模型参数。但是，当模型含有隐变量时，就不能简单地使用以上估计方法，而EM算法就是针对含有隐变量的概率模型参数的极大似然估计法。

一般地，用$X$表示可观测随机变量的数据，$Z$表示隐随机变量的数据，$X$和$Z$连在一起称为完全数据（complete-data），观测数据$X$又称为不完全数据（incomplete-data）。假设给定观测数据$X$，其概率分布是$P(X|\theta)$，其中$\theta$是需要估计的模型参数，那么不完全数据$X$的似然函数是$P(X|\theta)$，对数似然函数$L(\theta)=\log P(X|\theta)$；假设$X$和$Z$的联合概率分布是$P(X,Z|\theta)$，那么完全数据的对数似然函数是$\log P(X,Z|\theta)$。对于不完全数据的统计估计问题，EM算法已经成为了一种通用的工具。

从掷硬币实验说起

给定两枚硬币$A$和$B$，它们出现正面的概率分别为$\theta_A$和$\theta_B$(未知)，我们的目标是通过重复5次以下实验来估计$\theta=(\theta_A, \theta_B)$。

选择一枚硬币，并且知道具体是哪一枚，然后用选中的硬币掷十次，记录结果。因此，总共进行了50次掷硬币的实验。如下图所示

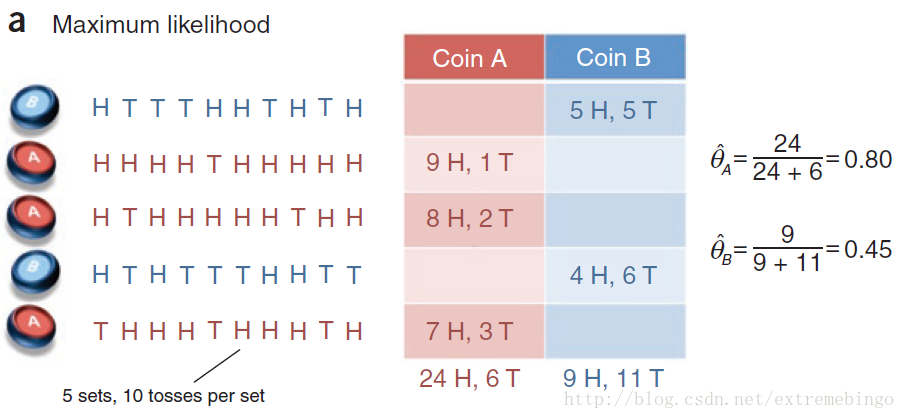
现在，引入两个随机变量$X=\{X_1,X_2,X_3,X_4,X_5\}$和$Z=\{Z_1,Z_2,Z_3,Z_4,Z_5\}$，其中$X_i\in\{0,1,\cdots,10\}$表示第$i$次实验硬币正面朝上的次数，$Z_i\in\{A,B\}$表示第$i$次实验所用的硬币。上述问题为完全数据的参数估计问题，可通过正面出现的比例进行估计

$$\hat{\theta_A}=\frac{\#\ of\ heads\ using\ coin\ A}{total\ \#\ of\ flips\ using\ coin\ A} \\ \hat{\theta_B}=\frac{\#\ of\ heads\ using\ coin\ B}{total\ \#\ of\ flips\ using\ coin\ B}$$

事实上，上述的估计方式就是统计学上的最大似然估计。

现在考虑一个更有挑战性的参数估计问题。只给定硬币出现正面的次数，而不给定是由哪一枚硬币掷出的，即$Z$为隐含变量。因此，该问题就转化为不完全数据的参数估计问题。此时，由于不知道具体是哪一枚硬币，所以无法通过直接计算硬币出现正面的次数来估计$\theta$。当概率模型存在隐变量时，不能简单地使用极大似然估计，需要采用下文的EM算法来计算模型参数。

凸函数

定义1 定义在区间$I=[a,b]$上的实函数$f$，如果对于$\forall x_1,x_2\in I, \lambda\in[0,1]$，函数$f$满足以下不等式

$$f(\lambda x_1 + (1-\lambda)x_2) \le \lambda f(x_1) + (1-\lambda)f(x_2) \tag{1}$$

则称函数$f$为凸函数。其几何解释如下图所示

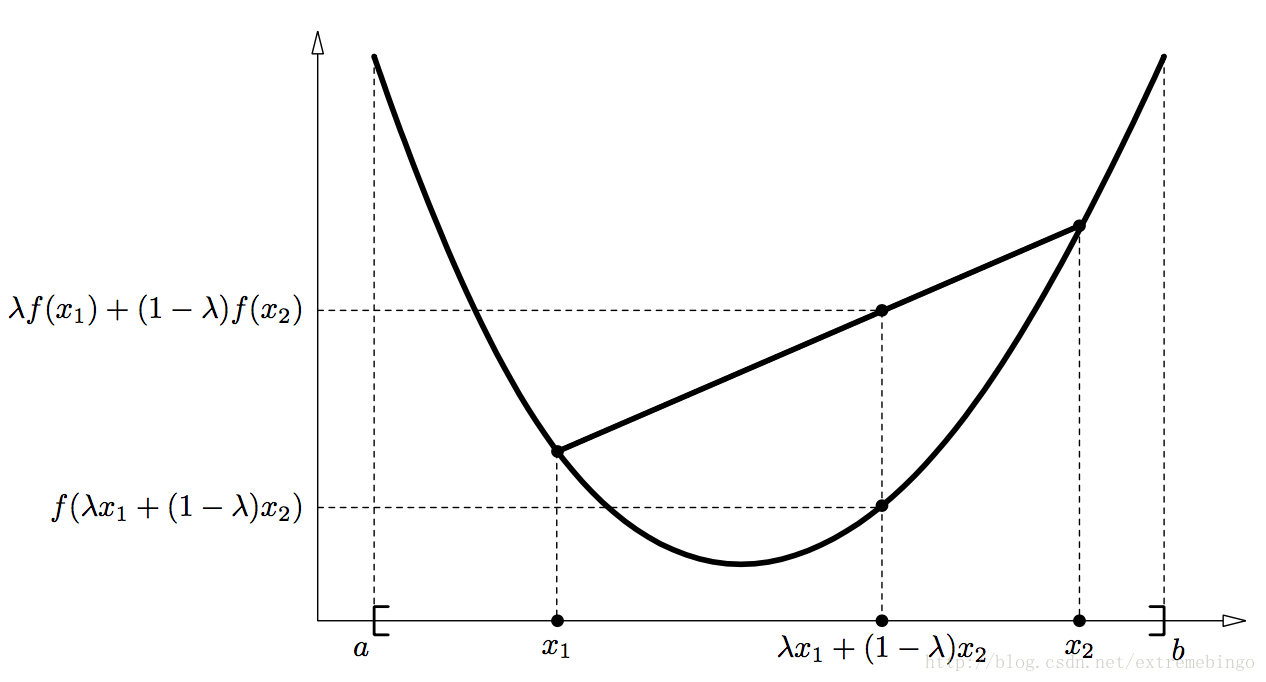
定义2 如果函数$-f$是凸函数，则函数$f$是凹函数。

定理1 如果函数$f$在区间$[a,b]$上二阶可导，并且$f^{''}(x)\ge0$，则$f$在区间$[a,b]$上为凸函数。

定理2(Jensen inequality) $f$为区间$[a,b]$上的凸函数，若$x_1,x_2,\cdots,x_n\in I$，并且$\lambda_1,\lambda_2,\cdots,\lambda_n\ge0, \sum_{i=1}^n=1$，则以下不等式成立

$$f(\sum_{i=1}^n\lambda_ix_i)\le \sum_{i=1}^n\lambda_if(x_i) \tag{2}$$

证明： 使用数学归纳法证明

1. 当$n=1$时，(2)式显然成立，并取得等号。
2. 当$n=2$时，即为凸函数的定义。
3. 假设当$n=n$时(2)式成立，则

$$\begin{align} f(\sum_{i=1}^{n+1}\lambda_ix_i) & = f(\lambda_{n+1}x_{n+1} + \sum_{i=1}^{n}\lambda_ix_i) \\ & = f(\lambda_{n+1}x_{n+1} + (1-\lambda_{n+1})\frac{1}{1-\lambda_{n+1}}\sum_{i=1}^{n}\lambda_ix_i) \\ & \le \lambda_{n+1}f(x_{n+1}) + (1-\lambda_{n+1})f(\frac{1}{1-\lambda_{n+1}}\sum_{i=1}^{n}\lambda_ix_i) ) \\ & = \lambda_{n+1}f(x_{n+1}) + (1-\lambda_{n+1})f(\sum_{i=1}^{n}\frac{\lambda_i}{1-\lambda_{n+1}}x_i) ) \\ & \le \lambda_{n+1}f(x_{n+1}) + (1-\lambda_{n+1})\sum_{i=1}^{n}\frac{\lambda_i}{1-\lambda_{n+1}}f(x_i) \\ & = \lambda_{n+1}f(x_{n+1}) + \sum_{i=1}^{n}\lambda_if(x_i) \\ & = \sum_{i=1}^{n+1}\lambda_if(x_i) \end{align}$$

得证。

因为$\lambda_1,\lambda_2,\cdots,\lambda_n\ge0, \sum_{i=1}^n=1$，所以当$X$为随机变量时，Jensen inequality可以写成

$$Ef(X) \ge f(EX) \tag{3}$$

图形表示为

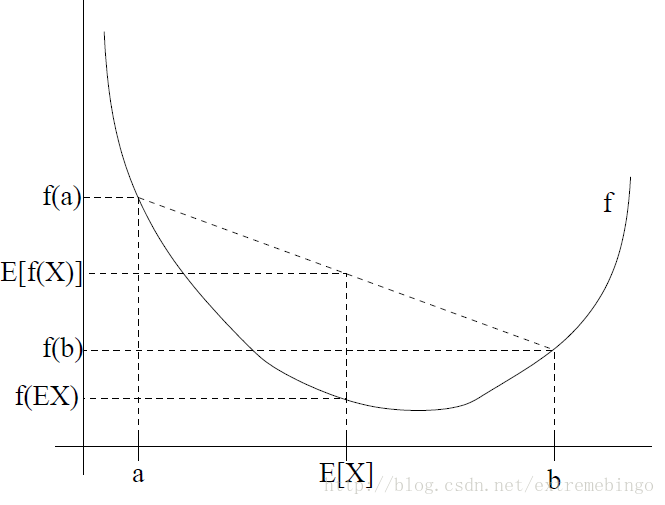
EM算法

对于含有隐含变量的数据，EM算法是一个用于计算最大概率的高效的迭代过程，我们希望通过估计得到的模型参数可以使得观测到的数据出现的可能性最大。

EM算法的导出

对于一个含有隐含变量$Z$的概率模型，假设有$m$个样本$\{x^{(1)},x^{(2)},\cdots,x^{(m)}\}$，目标是极大化观测数据（不完全数据）$X$关于参数$\theta$的对数似然函数，即极大化

$$\begin{align} l(\theta) & = \sum_{i=1}^{m}\log p(x;\theta) \\ & = \sum_{i=1}^{m} \log \sum_Z p(x,z;\theta) \tag{4} \end{align}$$
极大化的主要困难在于上式中存在隐变量。最大化的 $l(\theta)$很难求得，但是我们可以构造 $l(\theta)$的下边界(E-step)，然后优化该下边界(M-step)，不断重复以上过程。

令$Q_i$表示$z$的分布，满足条件$\sum_zQ_i(z) = 1, Q_i(z) \ge 0$

$$\begin{align} \sum_i \log p(x^{(i)}; \theta) & = \sum_i \log \sum_{z^{(i)}} p(x^{(i)}, z^{(i)}; \theta) \\ & = \sum_i \log \sum_{z^{(i)}} Q_i(z^{(i)}) \frac{p(x^{(i)}, z^{(i)}; \theta)}{Q_i(z^{(i)})} \\ & \ge \sum_i \sum_{z^{(i)}} Q_i(z^{(i)}) \log \frac{p(x^{(i)}, z^{(i)}; \theta)}{Q_i(z^{(i)})} \tag{5} \end{align}$$

最后一步是由Jensen inequality得到的。并且，$\sum_{z^{(i)}} Q_i(z^{(i)}) \log \frac{p(x^{(i)}, z^{(i)}; \theta)}{Q_i(z^{(i)})}$为$\frac{p(x^{(i)}, z^{(i)}; \theta)}{Q_i(z^{(i)})}$关于$z^{(i)}$的期望。

对于任意的分布$Q_i$，(5)式给出了$l(\theta)$的下边界。现在的问题是如何选择$Q_i$。

最直接的想法是，对于特定的$\theta$，使得下边界尽可能地靠近$l(\theta)$，即选择合适的$Q_i$，使得(5)式的等号成立。由Jensen inequality可知，若要使得等号成立，需满足以下条件

$$\frac{p(x^{(i)}, z^{(i)}; \theta)}{Q_i(z^{(i)})}=c$$

其中$c$不依赖于$z^{(i)}$。因此，只要使得

$$Q_i(z^{(i)}) \propto p(x^{(i)}, z^{(i)} ; \theta)$$

因为$Q_i$需满足$\sum_z Q_i(z^{(i)}) = 1$，因此可以取

$$\begin{align} Q_i(z^{(i)}) & = \frac{p(x^{(i)}, z^{(i)} ; \theta)}{\sum_z p(x^{(i)},z;\theta)} \tag{6} \\ & = \frac{p(x^{(i)}, z^{(i)} ; \theta)}{p(x^{(i)};\theta)} \\ & = p(z^{(i)} | x^{(i)} ; \theta) \tag{7} \end{align}$$

(6)式等号右边对$z^{(i)}$求和可以保证为1。

现在，通过将$Q_i$设置为(7)式，我们得到了(5)式的最大化下边界，这就是E-step。在M-step中，求得一个新的$\theta$，使得(5)式最大化。即

$$Repeat\ until\ convergence\ \{ \\ (E-step)\ For\ each\ i, \ set \ Q_i(z^{(i)}) := p(z^{(i)} | x^{(i)} ; \theta). \\ (M-step)\ Set\ \theta : = \arg \max_{\theta}\sum_i\sum_{z^{(i)}} Q_i(z^{(i)})\log \frac{p(x^{(i)}, z^{(i)}; \theta)}{Q_i(z^{(i)})} \\ \}$$

下图为迭代过程的图形化表示

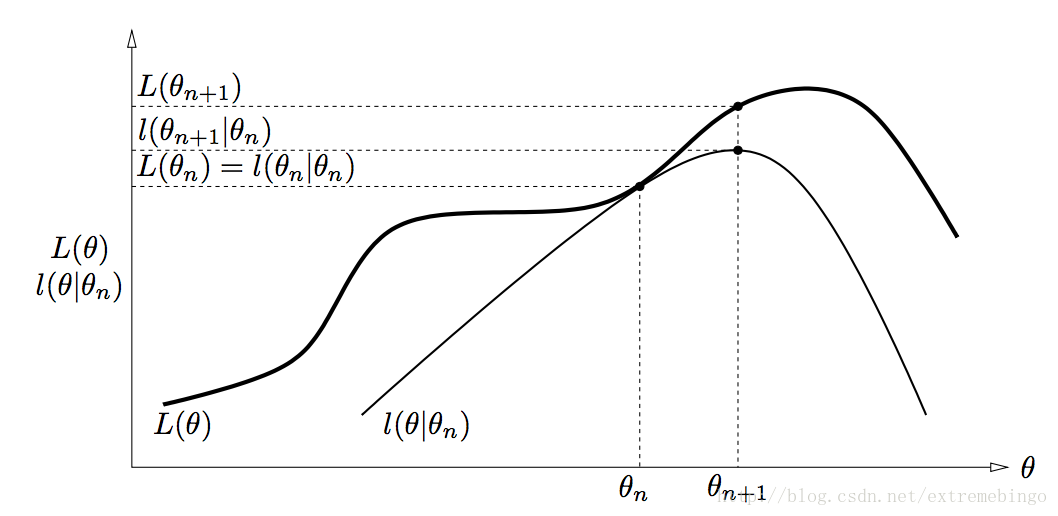
收敛性

假设参数$\theta^{(t)}$和$\theta^{(t+1)}$是由两个连续的迭代过程求得的，下面来证明EM算法的每一次迭代都会改善似然函数，即$l(\theta^{(t)}) \le l(\theta^{(t+1)})$。这个过程依赖$Q_i$的选择，当给定参数$\theta^{(t)}$时，设置$Q_i$为$Q_i^{(t)} := p(z^{(i)} | x^{(i)} ; \theta^{(t)})$，由此可通过(5)式得到

$$l(\theta^{(t)}) = \sum_i\sum_{z^{(i)}} Q_i^{(t)}(z^{(i)})\log \frac{p(x^{(i)}, z^{(i)}; \theta^{(t)})}{Q_i(z^{(i)})} \tag{8}$$

同样由式(5)可得

$$\begin{align} l(\theta^{(t+1)}) & \ge \sum_i \sum_{z^{(i)}} Q_i^{(t)}(z^{(i)}) \log \frac{p(x^{(i)}, z^{(i)}; \theta^{(t+1)})}{Q_i^{(t)}(z^{(i)})} \\ & \ge \sum_i \sum_{z^{(i)}} Q_i^{(t)}(z^{(i)}) \log \frac{p(x^{(i)}, z^{(i)}; \theta^{(t)})}{Q_i^{(t)}(z^{(i)})} \tag{9} \\ & = l(\theta^{(t)}) \end{align}$$

式(9)是因为$\theta^{(t+1)}$是由下式迭代得到的

$$\arg \max_{\theta}\sum_i\sum_{z^{(i)}} Q_i(z^{(i)})\log \frac{p(x^{(i)}, z^{(i)}; \theta)}{Q_i(z^{(i)})}$$

综上所述，$l(\theta)$单调递增。可以将在连续的两次迭代中，$l(\theta)$值的变化小于某一阈值作为停止迭代的条件。

note： EM算法只能保证参数估计序列收敛到对数似然函数序列的极大值点，不能保证收敛到最大值点。所以在应用中，初值的选择变得非常重要，常用的方法是选取几个不同的初值进行迭代，然后对得到的各个估计值加以比较，从中选择最好的。

再看掷硬币问题

其中一种迭代方式入下：

• 初始化参数$\hat{\theta^{(t)}}=(\hat{\theta_A^{(t)}}, \hat{\theta_B^{(t)}})$，同时初始化硬币$A$和$B$出现的概率（等概率）。

• 假设初始化的参数是正确的，通过最大似然估计计算模型参数$\hat{\theta^{(t+1)}}$.

• 重复以上两个过程直至收敛。

从理论公式推导高斯混合模型

随机变量$X$是由$k$个高斯分布混合而成，取得各个高斯分布的概率为$\phi_1, \phi_2, \cdots, \phi_k$，第$i$个高斯分布的均值为$\mu_i$，方差为$\Sigma_i$。若观测到随机变量$X$的一系列样本$\{x^{(1)}, x^{(2)}, \cdots, x^{(m)}\}$，试估计参数$\phi, \mu, \Sigma$。

E-step

$$w_j^{(i)} = Q_i(z^{(i)}=j) = p(z^{(i)}=j | x^{(i)}; \phi, \mu, \Sigma)$$

$w_j^{(i)}$表示第i个样本$x^{(i)}$属于第$j$个分模型的概率。

M-step

将多项分布和高斯分布的参数代入，并求解$\phi, \mu, \Sigma$使得式(5)取最大值，即

$$\begin{align} & \sum_{i=1}^m \sum_{z^{(i)}} Q_i(z^{(i)}) \log \frac{p(x^{(i)}, z^{(i)} ; \phi, \mu, \Sigma)}{Q_i(z^{(i)})} \\ & = \sum_{i=1}^m \sum_{j=1}^{k} Q_i(z^{(i)}=j) \log \frac{p(x^{(i)} | z^{(i)} = j ; \mu, \Sigma)p(z^{(i)} = j ; \phi)}{Q_i(z^{(i)} = j)} \\ & = \sum_{i=1}^m \sum_{j=1}^{k} w_j^{(i)} \log \frac{\frac{1}{(2\pi)^{n/2} |\Sigma_j|^{1/2}} \exp(-\frac{1}{2}(x^{(i)})-\mu_j)^T \Sigma_j^{-1} (x^{(i)})-\mu_j) \cdot \phi_j}{w_j^{(i)}} \tag{10} \end{align}$$

对高斯分布的均值$\mu_l$求偏导

$$\begin{align} & \nabla_{\mu_l} \sum_{i=1}^m \sum_{j=1}^{k} w_j^{(i)} \log \frac{\frac{1}{(2\pi)^{n/2} |\Sigma_j|^{1/2}} \exp(-\frac{1}{2}(x^{(i)}-\mu_j)^T \Sigma_j^{-1} (x^{(i)}-\mu_j) \cdot \phi_j}{w_j^{(i)}} \\ & = -\nabla_{\mu_l} \sum_{i=1}^m \sum_{j=1}^{k} w_j^{(i)} \frac{1}{2} (x^{(i)}-\mu_j)^T \Sigma_j^{-1} (x^{(i)}-\mu_j) \\ & = \frac{1}{2} \sum_{i=1}^m w_j^{(i)} \nabla_{\mu_l}2(\mu_l^T\Sigma_l^{-1}x^{(i)} - \mu_l^T\Sigma_l^{-1}\mu_l) \\ & = \sum_{i=1}^m w_j^{(i)} (\Sigma_l^{-1}x^{(i)} - \Sigma_l^{-1}\mu_l) \end{align}$$

令其等于0可得

$$\mu_l := \frac{\sum_{i=1}^mw_l^{(i)}x^{(i)}}{\sum_{i=1}^mw_l^{(i)}} \tag{11}$$

同理，对高斯分布的方差求偏导可得

$$\Sigma_j := \frac{\sum_{i=1}^{m}w_j^{(i)}(x^{(i)} - \mu_j)(x^{(i)} - \mu_j)^T} {\sum_{i=1}^{m}w_j^{(i)}} \tag{12}$$

求多项分布的参数$\phi$，删除(10)式中的常数项，得

$$\sum_{i=1}^m \sum_{j=1}^{k} w_j^{(i)} \log \phi_j \\ s.t.\ \sum_{j=1}^k \phi_j = 1$$

由于$log(\cdot)$已经约束了$\phi_j>0$，所以约束条件中没有该约束。

建立拉格朗日方程

$$L(\phi) = \sum_{i=1}^{m}\sum_{j=1}^{k} w_j^{(i)} \log \phi_j + \beta(\sum_{j=1}^k \phi_j - 1) \tag{13}$$

对$\phi_j$求偏导，并令其等于0

$$\begin{align} \frac{\partial L(\phi)}{\partial \phi_j} = \sum_{i=1}^m \frac{w_j^{(i)}}{\phi_j} + \beta \\ -\beta = \sum_{i=1}^m \sum_{j=1}^k w_j^{(i)} = \sum_{i=1}^m1 = m \\ \phi_j = \frac{1}{m} \sum_{i=1}^{m} w_j^{(i)} \tag{14} \end{align}$$

至此，由EM算法求解出了高斯混合模型的所有参数(11)(12)(14)。

参考文献

[1] 李航. 统计学习方法[M]. 清华大学出版社, 2012
[2] Borman S. The expectation maximization algorithm-a short tutorial[J]. Submitted for publication, 2004: 1-9.
[3] Do C B. What is the expectation maximization algorithm?[J]. Nature Biotechnology, 2008, 26(8):897-9.
[4] Andrew Ng. CS229 Lecture notes: The EM algorithm.