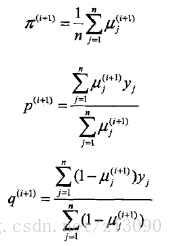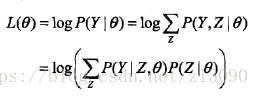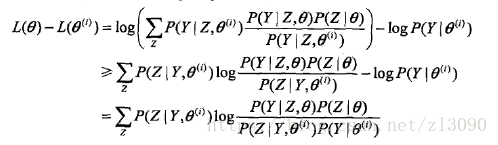【统计学习方法-李航-笔记总结】九、EM(Expectation Maximization期望极大算法)算法及其推广

本文是李航老师《统计学习方法》第九章的笔记，欢迎大佬巨佬们交流。

主要参考博客:

https://www.cnblogs.com/YongSun/p/4767517.html

https://blog.csdn.net/u010626937/article/details/75116000

主要包括以下内容：

1. EM算法的引入

2. EM算法的收敛性

3. EM算法在高斯混合学习模型中的应用

4. EM算法的推广

EM算法是一种迭代算法，用于含有隐变量(hidden variable)的概率模型参数的极大似然估计，或极大后验概率估计。EM算法的每次迭代由两步组成：E步，求期望(expectation)；M步，求极大( maximization )，所以这一算法称为期望极大算法(expectation maximization algorithm)，简称EM算法。

对于极大似然估计的补充：

极大似然估计，只是一种概率论在统计学中的应用，它是参数估计的方法之一。说的是已知某个随机样本满足某种概率分布，但是其中具体的参数不清楚，参数估计就是通过若干次实验，观察其结果，利用结果推出参数的大概值。最大似然估计是建立在这样的思想上：已知某个参数能使这个样本出现的概率值最大，我们当然不会再去选择其他小概率的样本，所以干脆就把这个参数作为估计的真实值。最大似然估计你可以把它看作是一个反推。多数情况下我们是根据已知条件来推算结果，而最大似然估计是已经知道了结果，然后寻求使该结果出现的可能性最大的条件，以此作为估计值。

求最大似然函数估计值的一般步骤：

（1） 写出似然函数；
（2） 对数似然函数取对数，并整理；
（3） 求导数，令导数为0，得到似然方程；
（4） 解似然方程，得到的参数即为所求。

最大（极大）似然估计也是统计学习中经验风险最小化（RRM）的例子。如果模型为条件概率分布，损失函数定义为对数损失函数，经验风险最小化就等价于最大似然估计。

对于几种估计的详述可参考前文：https://blog.csdn.net/zl3090/article/details/82989065

对于极大似然估计的例子可参考博客：https://blog.csdn.net/pipisorry/article/details/51461997?utm_source=blogxgwz0

1. EM算法的引入

概率模型又是既含有观测变量，又含有隐变量或潜在变量，如果概率模型的变量都是观测变量，那么给定数据，可以直接利用极大似然估计法，或贝叶斯估计法估计模型参数，但是当模型含有隐变量时，就不能简单地使用这些方法，EM算法就是含有隐变量的概率模型参数的极大似然估计法，或极大后验概率估计法。

（1）EM算法

三硬币模型：

求解过程：

三硬币模型可写作（一次实验后的结果）：

其中，y是观测变量，表示一次实验的结果是1或者0，z是隐变量，表示未观测到的硬币A的抛掷结果；

是参数模型，是以上数据的生成模型。

将观测数据表示为，未观测数据表示为，则观测数据的似然函数为：

求参数模型的极大似然估计，即

这个问题没有解析解，只有通过迭代的方法求解，EM算法就是可以用于求解这一问题的迭代算法。

按照EM算法，首先选取参数的初始值，记作，然后通过迭代计算参数估计值，直到收敛为止。

第i次迭代参数的估计值为：，第i+1次迭代为：

E步：计算观测数据yi来自硬币B的概率：

M步：计算模型参数的新估计值：

进行数字计算：

假设模型参数的初值为：

代入上述式子，得：

于是得到模型参数θ的极大似然估计：

如果选择不同的初值会有不同的结果，也就说明了EM算法与初值的选择有关。

一般地，用Y表示观测随机变量的数据，Z表示隐随机变量的数据。Y和Z连在一起称为完全数据( complete-data )，观测数据Y又称为不完全数据(incomplete-data)。假设给定观测数据Y，其概率分布是P(Y | θ)，其中θ是需要估计的模型参数，那么不完全数据Y的似然函数是P(Y | θ)，对数似然函数L(θ)=logP(Y | θ)；假设Y和Z的联合概率分布是P(Y, Z)，那么完全数据的对数似然函数是log P(Y, Z | θ)。

EM算法描述如下：

Q函数：完全数据的对数似然函数log P(Y, Z | θ)关于在给定观测数据Y和当前参数θ(i)下对未观测数据Z的条件概率分布P(Z | Y,θ(i))的期望称为Q函数，即

EM算法说明:

步骤(1)参数的初值可以任意选择。但需注意EM算法对初值是敏感的。

步骤(2) E步求Q( θ, θ(i))。Q函数式中Z是未观测数据，Y是观测数据。注意，Q( θ, θ(i))的第1个变量 θ表示要极大化的参数，第2个变量 θ(i)表示参数的当前估计值。每次迭代实际在求Q函数及其极大。

步骤(3) M步求Q( θ, θ(i))的极大化，得到 θ(i+1)，完成一次迭代 θ(i)--> θ(i+1)。后面将证明每次迭代使似然函数增大或达到局部极值。

步骤(4)给出停止迭代的条件，一般是对较小的正数，若满足则停止迭代。

（2）EM算法的导出

下边解释为什么EM算法可以实现对观测数据的极大似然估计：

对于一个含有隐变量的概率模型，目标是极大化观测数据（不完全数据），Y关于参数θ的对数似然函数，即极大化：

注意到这一极大化的主要困难是上式中有未观测数据（Z）并包含和（或积分）的对数。

事实上，EM算法是通过迭代逐步近似极大化L(θ)的，假设在第i次迭代后，θ的估计值是θ(i)，我们希望新估计值θ能使L(θ)增加，并逐步达到极大值，因此考虑两者的差：

利用Jensen不等式，得到其下界：（Jensen不等式详见https://baike.baidu.com/item/%E7%90%B4%E7%94%9F%E4%B8%8D%E7%AD%89%E5%BC%8F/397409?fr=aladdin）

令：

则：

因此，函数B是L的一个下界，任何使B增大的θ也可以使L增大，为了使L(θ)有尽可能大的增长，选择θ(i+1)是B达到极大，即：

上式等价于EM算法的一次迭代，即求Q函数及其极大化，下图给出EM算法的直观解释：

图中上方曲线为L(θ)，下方曲线为B(θ, θ(i))，为对数似然函数L(θ)的下界，且在 θ=θ(i)处相等。EM算法找到下一个点θ(i+1)使函数B(θ, θ(i))极大化，也使函数Q(θ, θ(i))极大化。函数B的增加，保证对数似然函数L在每次迭代中也是增加的。EM算法在点θ(i+1)重新计算Q函数值，进行下一次迭代。在这个过程中，对数似然函数L不断增大。从图可以推断出EM算法不能保证找到全局最优值。

（3）EM算法在非监督学习中的应用

训练数据只有输入没有对应的输出(X,？)，从这样的数据学习模型称为非监督学习问题。EM算法可以用于生成模型的非监督学习，生成模型由联合概率分布P(X, Y)表示，可以认为非监督学习训练数据是联合概率分布产生的数据。X为观测数据，Y为未观测数据。

2. EM算法的收敛性

EM算法的最大优点是简单性和普适性，下边探索EM算法得到的序列估计的收敛性：

定理：设P(Y | θ)为观测数据的似然函数，θ(i) (i=1, 2,...)为EM算法得到的参数估计序列，P(Y | θ(i) )(i=1, 2,...))为对应的似然函数序列，则P(Y | θ(i) )是单调递增的，即：

定理：设P(Y | θ)为观测数据的似然函数，θ(i) (i=1, 2,...)为EM算法得到的参数估计序列，L(θ(i))=P(Y | θ(i) )(i=1, 2,...))为对应的似然函数序列，

(1)如果P(Y | θ)有上界，则L(θ(i))收敛到某一值L*;

(2)在函数Q与L满足一定条件下，由EM算法得到的参数估计序列θ(i)的收敛值θ*是L(θ)的稳定点。

EM算法的收敛性包含关于对数似然函数序列L的收敛性和关于参数估计序列θ的收敛性两层意思，前者并不蕴涵后者。此外，定理只能保证参数估计序列收敛到对数似然函数序列的稳定点，不能保证收敛到极大值点。所以在应用中，初值的选择变得非常重要，常用的办法是选取几个不同的初值进行迭代，然后对得到的各个估计值加以比较，从中选择最好的。

3. EM算法在高斯混合学习模型中的应用

EM算法的一个重要应用是高斯混合模型的参数估计。

高斯混合模型：高斯混合模型是指具有如下形式的概率分布模型：，

高斯混合模型参数估计中的EM算法：

假设观测数据由上述高斯模型生成，我们利用EM算的估计高斯混合模型的参数θ:

(1) 明确隐变量，写出完全数据的对数似然函数：

可以设想观测数据yj是这样产生的：首先依概率ak选择第k个高斯分布分模型；然后依第k个分模型的概率分布生成观测

数据yj。这时观测数据yj是已知的；反映观测数据yj来自第k个分模型的数据是未知的，k=1,2,... ,K，为隐变量定义如下：

有了观测数据yi及未观测数据 $\gamma _{ik}$ ，那么完全数据是：

于是，完全数据的似然函数是：

其中，

那么，完全数据的对数似然函数为：

（2）EM算法的E步：确定Q函数

（3）确定EM算法的M步：

迭代的M步是求函数Q的极大值，即求新一轮迭代的模型参数：

通过求偏导并令其为0，可以得到：

其中，得到的。

高斯混合模型参数估计的EM算法：

4. EM算法的推广

EM算法还可以理解为F函数的极大-极大算法，基于这个解释有若干变形与推广，如广义期望极大（GEM算法）等。

（1）F函数的极大-极大算法

F函数：假设隐变量数据Z的概率分布为 $\widetilde{P}(Z)$ ，定义分布 $\widetilde{P}$ 与参数θ的函数F( $\widetilde{P}$ ,θ)如下：

称为F函数，式中是分布 $\widetilde{P}(Z)$ 的熵。

引理1：对于固定的θ，存在唯一的分布 $\widetilde{P}_{\theta }$ 极大化 $F(\widetilde{P},\theta )$ ，这时 $\widetilde{P}_{\theta }$ 由下式给出：，并且 $\widetilde{P}_{\theta }$ 随θ连续变化。

引理2：若，则

定理1：设L(θ) = logP(Y|θ)为观测数据的对数似然函数， $\theta ^{(i)}$ ,i =1,2,...,为EM算法得到的参数估计序列，函数 $F(\widetilde{P},\theta )$ 由上述F函数定义，如果 $F(\widetilde{P},\theta )$ 在 $\widetilde{P}^*$ 和 $\theta ^*$ 有局部极大值，那么L(θ)也在 $\theta ^*$ 有局部极大值；如果 $F(\widetilde{P},\theta )$ 在 $\widetilde{P}^*$ 和 $\theta ^*$ 达到全局最大值，那么L(θ)也在 $\theta ^*$ 达到全局最大值。

定理2：EM算法的一次迭代可以由F函数的极大-极大算法实现，设 $\theta ^{(i)}$ 为第i次迭代参数θ的估计， $\widetilde{P}^{(i)}$ 为第i次迭代函数 $\widetilde{P}$ 的估计，在第i+1次迭代的两步为：

（1）对固定的 $\theta ^{(i)}$ ，求 $\widetilde{P}^{(i+1)}$ 使 $F(\widetilde{P},\theta^{(i)} )$ 极大化;

（2）对固定的 $\widetilde{P}^{(i+1)}$ ，求 $\widetilde{\theta }^{(i+1)}$ 使 $F(\widetilde{P^{i+1}},\theta )$ 极大化;

（2）GEM算法

算法1：

在GEM算法1中，有时求Q(theta，theta(i))的极大化是很困难的。 GEM算法2和GEM算法3并不是直接求theta(i+1)使Q达到极大的theta，而是找一个theta(i+1)使得Q(theta(i+1), theta(i)) >Q(theta(i), theta(i))。

算法2：

算法3：

【统计学习方法-李航-笔记总结】九、EM(Expectation Maximization期望极大算法)算法及其推广

猜你喜欢