版权声明:欢迎大家转载分享,转载请注明出处,有需要请留言联系我~~~ https://blog.csdn.net/crazyice521/article/details/53257991
一、算法简介
最大期望算法(Expectation Maximization Algorithm,又译期望最大化算法),是一种迭代算法,用于含有隐变量(latent variable)的概率参数模型的最大似然估计或极大后验概率估计。
极大似然估计只是一种概率论在统计学的应用,它是参数估计的方法之一。说的是已知某个随机样本满足某种概率分布,但是其中具体的参数不是很清楚,参数估计就是通过若干次的实验,观察每一次的结果,利用得到的结果去分析、推测出参数的大概的值。最大似然估计就是建立在这样的思想上:已知某个参数能使这个样本出现的概率最大,我们当然不会再去选择其他小概率的样本,所以就干脆直接把换个参数当作估计到的真实值。
求最大似然估计值的一般步骤
①写出似然函数
②对似然函数取对数,整理函数形式
③对变量进行求导,使倒数等于0,得到似然方程
④求解似然方程,得到的参数即为所求。
二、算法详解
假设我们想要知道A和B两个参数,在一开始的情况下,A、B两者都是不知道的,但是假设我们在知道了A的信息之后,就可以直接求得B的信息,反过来也是一样的,知道B也可以直接求得A。那么此时,我们就可以考虑首先对两者中的任何一个赋予某种初值,从而可以得到另一个的估计值,然后由得到的估计值再去计算另外一个的值,然后对两个值的错误率设置一个阈值或者停止条件,直到收敛停止这个过程,得到我们所要求得的两个值A和B。
算法流程
①初始化分布参数θ
重复以下步骤:
E步:根据参数初始值或上一次迭代的模型参数来计算出隐性变量的后验概率,其实就是隐性变量的期望。作为隐性变量的现估计值:
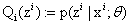
M步:将似然函数最大化以获得新的参数值:
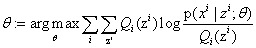
EM的另外一种直观的理解:
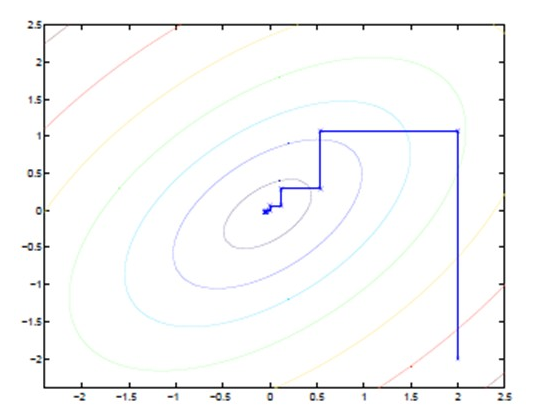
途中的直线式迭代优化的路径,可以从图中看到,每一步都会想着最优值前进一步,而且前进路线是平行于坐标轴的,因为每一步都是固定一个变量去优化另外一个变量。这犹如在x-y坐标系中找一个曲线的极值,然而曲线函数不能直接求导,因此什么梯度下降方法就不适用了。但固定一个变量后,另外一个可以通过求导得到,因此可以使用坐标上升法,一次固定一个变量,对另外的求极值,最后逐步逼近极值。对应到EM上,E步:固定θ,优化Q;M步:固定Q,优化θ;交替将极值推向最大。
三、几个概念
不得不吐槽一下CSDN的公式编辑真是一大难题,这个只能放上我的手写体了~~~丑了点,但是,应该能看的懂吧~吧~(没自信+1)

设f是定义域为实数的函数,如果对于所有的实数x。如果对于所有的实数x,f(x)的二次导数大于等于0,那么f是凸函数。当x是向量时,如果其hessian矩阵H是半正定的,那么f是凸函数。如果只大于0,不等于0,那么称f是严格凸函数。
Jensen不等式
Jensen不等式表述如下:
如果f是凸函数,X是随机变量,那么:E[f(X)]>=f(E[X])
特别地,如果f是严格凸函数,当且仅当X是常量时,上式取等号。
如果用图表示会很清晰:

图中,实线f是凸函数,X是随机变量,有0.5的概率是a,有0.5的概率是b。(就像掷硬币一样)。X的期望值就是a和b的中值了,图中可以看到E[f(X)]>=f(E[X])成立。 当f是(严格)凹函数当且仅当-f是(严格)凸函数。Jensen不等式应用于凹函数时,不等号方向反向。
