EM算法（Expectation Maximization Algorithm）

1. Jensen不等式

设 f 是定义域为实数的函数，如果对于所有的实数 x， $f^{^{''}}(x)\geq 0$ ，那么 f 是凸函数。当 x 是向量时，如果其hessian矩阵 H 是半正定的（ $H\geq 0$ ），那么 f 是凸函数。如果 $f^{^{''}}(x)> 0$ 或者 $H> 0$ ，那么称 f 是严格凸函数。

Jensen不等式表述如下：

如果 f 是凸函数，X是随机变量，那么 $E[f(X)]\geq f(EX)$

特别地，如果 f 是严格凸函数，那么 $E[f(X)]= f(EX)$ ，当且仅当 $p(X=E[X])=1$ ，也就是说 x 是常量。这里我们将 $f(E[X])$ 简写为 $f(EX)$ 。

2. 最大似然估计

目标：找出与样本的分布最接近的概率分布模型

概率密度p(x|θ)是高斯分布N(u,∂)的形式,未知参数是θ=[u, ∂]T。抽到的样本集是X={x1,x2,…,xN},其中，均值u、方差∂2

最大似然函数是在未知参数是θ的情况下，估计样本X的类别，用联合概率形式为：

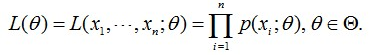
这个概率反映了在概率密度函数的参数是θ时，得到X这组样本的概率。即：参数θ相对于样本集X的似然函数（likehood function）。记为L(θ)。

EM算法推导过程中，会使用到极大似然估计法估计参数，所以，首先给出一个求最大似然函数估计值的一般步骤：

（1）写出似然函数；

（2）对似然函数取对数，并整理；

（3）求导数，令导数为0，得到似然方程；

（4）解似然方程，得到的参数即为所求；

3. EM算法

EM算法是求极大似然借的一种算法。

给定m个训练样本{x(1),…,x(m)x(1),…,x(m)},假设样本间相互独立，我们想要拟合模型p(x,z)p(x,z)到数据的参数。根据分布，我们可以得到如下这个似然函数：

第一步是对极大似然函数取对数，第二步是对每个样本实例的每个可能的类别z求联合分布概率之和。然而，直接求这个参数θ会比较困难，因为上式存在一个隐含随机变量（latent random variable）z。如果z是个已知的数，那么使用极大似然估计来估算会很容易。在这种z不确定的情形下，EM算法就派上用场了。

EM算法的核心思想，简单的归纳一下：

（1）EM算法通过引入隐含变量,使用MLE（极大似然估计）进行迭代求解参数。

（2）通常引入隐含变量后会有两个参数，EM算法首先会固定其中的第一个参数，然后使用MLE计算第二个变量值；

（3）接着通过固定第二个变量，再使用MLE估测第一个变量值；

（3）依次迭代，直至收敛到局部最优解。

由于算法保证了每次迭代之后，似然函数都会增加，所以函数最终会收敛。

更加直观的表示EM算法迭代过程如下图：