参考:
1.如何感性地理解EM算法?
2.EM算法实例及Python实现
一、一个简单的概率问题
实验:现在有A和B两个硬币,我们从这两个硬币中,随机选取5次,做5组实验,每组实验内容是:抛出所选的硬币,记录正反面。
实验数据如下:
目标:根据所得到的实验数据,分别求出硬币A和B抛出后正面向上的概率。
根据古典概率的原理,容易求出:
硬币A正面向上的概率为 PA = (9 + 8 + 7) / (10*3) = 0.8
硬币B正面向上的概率为 PB = (5 + 4) / (10*2) = 0.45
二、如果不知道所选择的的硬币呢
如果不知道所选取的硬币是A还是B,只记录硬币抛下后的正反面,那么记录的数据如下:
在这种情况下,目标相同:根据上面的实验数据,分别求出硬币A和B抛出后正面向上的概率。
EM算法的做法如下:
随机设置PA = 0.8, PB = 0.6,我们计算一下,针对每次实验,我们分别假设是硬币A还是B,然后计算出现对应实验结果的概率。比如针对第一次实验,假设选择的硬币是A,那么出现对应的实验结果(5正5反)的概率为:
0.8^5*(1-0.8)^5
如此,计算对应的概率分别为:
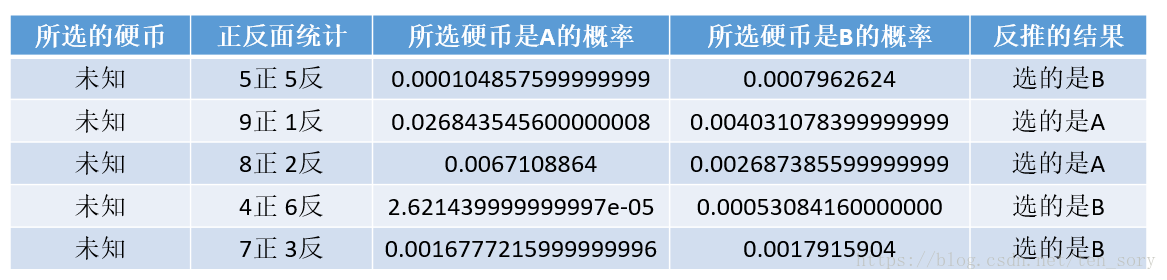
因此,计算PA和PB:
PA = (9 + 8) / (10 * 2) = 0.85
PB = (5 + 4 + 7) / (10 * 3) = 0.5333...
可以看出这和之前假设的PA = 0.85, PB = 0.6有所不同。这个过程是一个迭代的过程,一直用上面的方法,更新PA和PB,直到收敛,得到的PA和PB就是最终的答案。
上述问题的Python代码如下:
import numpy as np
if __name__ == '__main__':
n, m = 5, 10 # 5组实验,每组10次
nzs = [5, 9, 8, 4, 7] # 每组实验,硬币正面的次数
# 初始化
PA = 0.8 # 待求的概率:抛硬币A正面向上的概率
PB = 0.6 # 待求的概率:抛硬币B正面向上的概率
n_iter = 10
for i in range(0, n_iter): # 迭代多次
selected_coins = []
for j in range(0, n):
# P_A 记录的是,如果第j次实验,选择的是硬币A,那么出现对应的实验结果的概率
P_A = np.power(PA, nzs[j])*np.power(1-PA, m-nzs[j])
P_B = np.power(PB, nzs[j])*np.power(1-PB, m-nzs[j])
if P_A > P_B:
selected_coins.append('A')
else:
selected_coins.append('B')
fenzi = [0, 0]
fenmu = [0, 0]
for j, x in enumerate(selected_coins):
if x == 'A':
fenzi[0] += nzs[j]
fenmu[0] += m
else:
fenzi[1] += nzs[j]
fenmu[1] += m
PA = fenzi[0] / fenmu[0]
PB = fenzi[1] / fenmu[1]
print(PA, PB)迭代10次之后,运行结果如下:
可以看出,第二次就收敛了。真实的值是PA = 0.8, PB = 0.45。EM算法求得结果与实际结果有差别。
三、小结
上述过程,可以归纳为如下几个步骤:
step1. 随机设置PA和PB的值
step2. 反推所取的硬币是A还是B(Maximum)
step3. 根据反推的结果重新计算PA和PB(Expectation)
step4. 迭代上述过程
以上就是期望最大化的过程。其中step2,“反推”的过程采用的是极大似然估计。
四、改进的方法
上述案例中,step2“反推”的过程采用极大似然估计,“反推”所选取的硬币是A还是B,改进的方法是:将概率归一化如下:
针对第一组数据,此时不再根据 0.116 < 0.884,直接判定,第一组选择的硬币是B,而是说,选择硬币A的概率是0.116,选择硬币B的概率是0.884。
在这种情况下,PA的计算方法如下:
PA = 正面的情况 / [正面的情况 + (反面的情况)]
正面的情况 = (5*0.116 + 9*0.869 + 8*0.714 + 4*0.0471 + 7*0.484)
反面的情况 = (5*0.116 + 1*0.869 + 2*0.714 + 4(0.0471 + 3*0.484)
正面的情况 + 反面的情况 = 10 * (0.116 + 0.869 + 0.714 + 0.0471 + 0.484)
对应的代码如下:
import numpy as np
if __name__ == '__main__':
n, m = 5, 10 # 5组实验,每组10次
nzs = [5, 9, 8, 4, 7] # 每组实验,硬币正面的次数
# 初始化
PA = 0.8 # 待求的概率:抛硬币A正面向上的概率
PB = 0.6 # 待求的概率:抛硬币B正面向上的概率
n_iter = 10
for i in range(0, n_iter): # 迭代多次
selected_coins_p_a = []
selected_coins_p_b = []
for j in range(0, n):
# P_A 记录的是,如果第j次实验,选择的是硬币A,那么出现对应的实验结果的概率
P_A = np.power(PA, nzs[j])*np.power(1-PA, m-nzs[j])
P_B = np.power(PB, nzs[j])*np.power(1-PB, m-nzs[j])
# 归一化
P_A = P_A / (P_A + P_B)
P_B = 1 - P_A
selected_coins_p_a.append(P_A)
selected_coins_p_b.append(P_B)
#
# print('P_A', P_A)
# print('P_B', P_B)
# exit()
zhengmian, fanmian = 0, 0
for j in range(0, n):
zhengmian += nzs[j] * selected_coins_p_a[j]
fanmian += (m - nzs[j]) * selected_coins_p_a[j]
PA = zhengmian / (zhengmian + fanmian)
zhengmian, fanmian = 0, 0
for j in range(0, n):
zhengmian += nzs[j] * selected_coins_p_b[j]
fanmian += (m - nzs[j]) * selected_coins_p_b[j]
PB = zhengmian / (zhengmian + fanmian)
print(PA, PB)运行结果如下:
真实结果是0.8, 0.45。同样是迭代10次,改进之前的结果是0.85, 0.53。改进之后的结果是0.79, 0.51,更接近真实值。
本文通过简单的案例,理解了EM算法背后的原理。