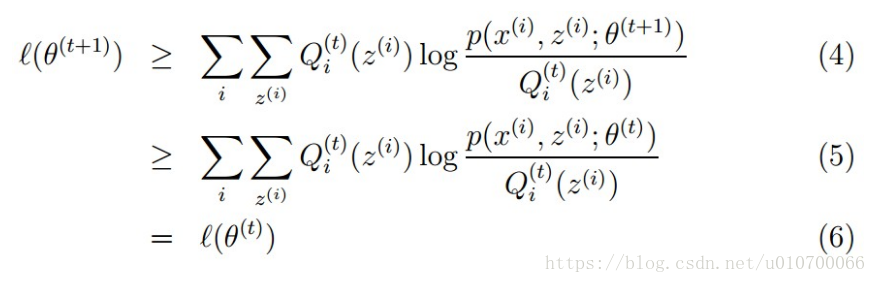机器学习十大算法之六：EM(Expectation Maximization)算法

一、EM由来

很多时候对EM算法产生疑惑是不清楚这个算法是怎么来的，为什么这样；又有什么样的用途。其实EM是一种以迭代的方式来解决一类特殊最大似然 (Maximum Likelihood) 问题的方法，这类问题通常是无法直接求得最优解，但是如果引入隐含变量(就是给这个存在但是具体值多少未知的变量一个假设的值)，在已知隐含变量的值的情况下，就可以转化为简单的情况，直接求得最大似然解。所以要理解为啥要有EM算法，就要先理解极大似然估计；

二、极大似然

概念：
最大似然估计是个概率学的问题，其作用是对一次采样的数据（包含了很多特征信息点，知道其满足什么分布，如高斯分布，但参数未知，从而转换为一个参数估计的问题），最大似然估计的作用是，利用一次采样的数据（不完整的数据，以抛硬币的例子来说明最贴切），再通过对应的模型（比如抛硬币一般就是二项分布，男女身高比例一般都是符合高斯分布）来估计完整数据的真实分布（给定模型二项，高斯求他们的具体参数），但该估计是最大可能的估计，而不是无偏估计。

以下部分转载自从最大似然到EM算法浅解 ;由于文章清晰易懂，就将其转载过来；如有侵权，请告诉我。有部分根据自己理解修改。

举例：
$~~~~$假设调查学校的男生和女生的身高分布（调查身高符合自然界规律，一般就是高斯分布了）。你怎么做啊？
你说那么多人不可能一个一个去问吧，肯定是抽样了。
$~~~~$ 假设你在校园里随便地活捉了100个男生和100个女生。他们共200个人（也就是200个身高的样本数据）。那下一步怎么办啊？你开始喊：“男的左边，女的右边，其他的站中间！”。然后你就先统计抽样得到的100个男生的身高。假设他们的身高是服从高斯分布的（这个）。但是这个分布的均值u和方差∂2我们不知道，这两个参数就是我们要估计的。记作$θ=[u, ∂]^T$
$~~~~$用数学的语言来说：在学校那么多男生（身高）中，我们独立地按照概率密度p(x|θ)抽取了100个（身高），组成样本集X，我们想通过样本集X来估计出未知参数θ。这里概率密度p(x|θ)我们知道了是高斯分布N(u,∂)的形式，其中的未知参数是$θ=[u, ∂]^T$。抽到的样本集是$X={x_1,x_2,…,x_N}$，其中$x_i$表示抽到的第$i$个人的身高，这里N就是100，表示抽到的样本个数。
$~~~~$由于每个样本都是独立地从p(x|θ)中抽取的，换句话说这100个男生中的任何一个，都是我随便捉的，从我的角度来看这些男生之间是没有关系的。那么，我从学校那么多男生中为什么就恰好抽到了这100个人呢？抽到这100个人的概率是多少呢？因为这些男生（的身高）是服从同一个高斯分布p(x|θ)的。那么我抽到男生A（的身高）的概率是$p(x_A|θ)$，抽到男生B的概率是$p(x_B|θ)$，那因为他们是独立的，所以很明显，我同时抽到男生A和男生B的概率是$p(x_A|θ)*p(x_B|θ)$，同理，我同时抽到这100个男生的概率就是他们各自概率的乘积了。用数学家的口吻说就是从分布是p(x|θ)的总体样本中抽取到这100个样本的概率，也就是样本集X中各个样本的联合概率，用下式表示：

$$L(θ)=L(x_1,x_2,...,x_n;θ)=\prod_{i=1}^np(x_i;θ)$$

这个概率反映了，在概率密度函数的参数是θ时，得到X这组样本的概率。因为这里X是已知的，也就是说我抽取到的这100个人的身高可以测出来，也就是已知的了。而θ是未知了，则上面这个公式只有θ是未知数，所以它是θ的函数。这个函数反映的是在不同的参数θ取值下，取得当前这个样本集的可能性，因此称为参数θ相对于样本集X的似然函数（likehood function）。记为L(θ)。

$~~~~$这里出现了一个概念，似然函数。还记得我们的目标吗？我们需要在已经抽到这一组样本X的条件下，估计参数θ的值。怎么估计呢？似然函数有啥用呢？那咱们先来了解下似然的概念。
$~~~~$某位同学与一位猎人一起外出打猎，一只野兔从前方窜过。只听一声枪响，野兔应声到下，如果要你推测，这一发命中的子弹是谁打的？你就会想，只发一枪便打中，由于猎人命中的概率一般大于这位同学命中的概率，看来这一枪是猎人射中的。
$~~~~$这个例子所作的推断就体现了极大似然法的基本思想。

回到男生身高那个例子。在学校那么男生中，我一抽就抽到这100个男生（表示身高），而不是其他人，那是不是表示在整个学校中，这100个人（的身高）出现的概率最大啊。那么这个概率怎么表示？哦，就是上面那个似然函数L(θ)。所以，我们就只需要找到一个参数θ，其对应的似然函数L(θ)取到最大，也就是说抽到这100个男生（的身高）概率最大。这个叫做θ的最大似然估计量，记为：

$$\hat θ= \arg \max _θ L(θ) ---(表示求能让函数L(θ)取得最大的参数θ是多少)$$
$~~~~$ 有时，可以看到L(θ)是连乘的，所以为了便于分析，还可以定义对数似然函数，将其变成连加的：
$$H(θ)= \ln L(θ)= \ln L(x_1,x_2,...,x_n;θ)=\sum_{i=1}^n \ln p(x_i;θ)$$
$~~~~$好了，现在我们知道了，要求θ，只需要使θ的似然函数L(θ)极大化，然后极大值对应的θ就是我们的估计。这里就回到了求最值的问题了。怎么求一个函数的最值？当然是求导，然后让导数为0，那么解这个方程得到的θ就是了（当然，前提是函数L(θ)连续可微）。那如果θ是包含多个参数的向量那怎么处理啊？当然是求L(θ)对所有参数的偏导数，也就是梯度了，那么n个未知的参数，就有n个方程，方程组的解就是似然函数的极值点了，当然就得到这n个参数了。

$~~~~$最大似然估计你可以把它看作是一个反推。多数情况下我们是根据已知条件(概率模型，模型参数)来推算结果，而最大似然估计是已经知道了结果(概率模型，抽样数据)，然后寻求使该结果出现的可能性最大的条件，以此作为估计值。

$~~~~$极大似然估计，只是一种概率论在统计学的应用，它是参数估计的方法之一。说的是已知某个随机样本满足某种概率分布，但是其中具体的参数不清楚，参数估计就是通过若干次试验，观察其结果，利用结果推出参数的大概值。最大似然估计是建立在这样的思想上：已知某个参数能使这个样本出现的概率最大，我们当然不会再去选择其他小概率的样本，所以干脆就把这个参数作为估计的真实值。

求最大似然函数估计值的一般步骤：

（1）写出似然函数；

（2）对似然函数取对数，并整理；

（3）求导数，令导数为0，得到似然方程；

（4）解似然方程，得到的参数即为所求；

三、EM算法原理

$~~~~$好了，重新回到上面那个身高分布估计的问题。现在，通过抽取得到的那100个男生的身高和已知的其身高服从高斯分布，我们通过最大化其似然函数，就可以得到了对应高斯分布的参数θ=[u, ∂]T了。那么，对于我们学校的女生的身高分布也可以用同样的方法得到了。

$~~~~$再回到例子本身，如果没有“男的左边，女的右边，其他的站中间！”这个步骤，或者说我抽到这200个人中，某些男生和某些女生一见钟情，已经好上了，纠缠起来了。咱们也不想那么残忍，硬把他们拉扯开。那现在这200个人已经混到一起了，这时候，你从这200个人（的身高）里面随便给我指一个人（的身高），我都无法确定这个人（的身高）是男生（的身高）还是女生（的身高）。也就是说你不知道抽取的那200个人里面的每一个人到底是从男生的那个身高分布里面抽取的，还是女生的那个身高分布抽取的。用数学的语言就是，抽取得到的每个样本都不知道是从哪个分布抽取的。

$~~~~$这个时候，对于每一个样本或者你抽取到的人，就有两个东西需要猜测或者估计的了，一是这个人是男的还是女的？二是男生和女生对应的身高的高斯分布的参数是多少？

$~~~~$只有当我们知道了哪些人属于同一个高斯分布的时候，我们才能够对这个分布的参数作出靠谱的预测，例如刚开始的最大似然所说的，但现在两种高斯分布的人混在一块了，我们又不知道哪些人属于第一个高斯分布，哪些属于第二个，所以就没法估计这两个分布的参数。反过来，只有当我们对这两个分布的参数作出了准确的估计的时候，才能知道到底哪些人属于第一个分布，那些人属于第二个分布。

$~~~~$这就成了一个先有鸡还是先有蛋的问题了。鸡说，没有我，谁把你生出来的啊。蛋不服，说，没有我，你从哪蹦出来啊。（呵呵，这是一个哲学问题。当然了，后来科学家说先有蛋，因为鸡蛋是鸟蛋进化的）。为了解决这个你依赖我，我依赖你的循环依赖问题，总得有一方要先打破僵局，说，不管了，我先随便整一个值出来，看你怎么变，然后我再根据你的变化调整我的变化，然后如此迭代着不断互相推导，最终就会收敛到一个解。这就是EM算法的基本思想了。

$~~~~~~~~$EM算法就是这样，假设我们想估计知道A和B两个参数，在开始状态下二者都是未知的，但如果知道了A的信息就可以得到B的信息，反过来知道了B也就得到了A。可以考虑首先赋予A某种初值，以此得到B的估计值，然后从B的当前值出发，重新估计A的取值，这个过程一直持续到收敛为止。

$~~~~~~~~$EM的意思是“Expectation Maximization”，在我们上面这个问题里面，我们是先随便猜一下男生（身高）的正态分布的参数：如均值和方差是多少。例如男生的均值是1米7，方差是0.1米（当然了，刚开始肯定没那么准），然后计算出每个人更可能属于第一个还是第二个正态分布中的（例如，这个人的身高是1米8，那很明显，他最大可能属于男生的那个分布），这个是属于Expectation一步。有了每个人的归属，或者说我们已经大概地按上面的方法将这200个人分为男生和女生两部分，我们就可以根据之前说的最大似然那样，通过这些被大概分为男生的n个人来重新估计第一个分布的参数，女生的那个分布同样方法重新估计。这个是Maximization。然后，当我们更新了这两个分布的时候，每一个属于这两个分布的概率又变了，那么我们就再需要调整E步……如此往复，直到参数基本不再发生变化为止。

$~~~~~~~~$这里把每个人（样本）的完整描述看做是三元组$y_i=\{x_i,z_{i1},z_{i2}\}$，其中，$x_i$是第i个样本的观测值，也就是对应的这个人的身高，是可以观测到的值。$z_{i1}$和$z_{i2}$表示男生和女生这两个高斯分布中哪个被用来产生值$x_i$，就是说这两个值标记这个人到底是男生还是女生（的身高分布产生的）。这两个值我们是不知道的，是隐含变量。确切的说，$z_{ij}$在$x_i$由第j个高斯分布产生时值为1，否则为0。例如一个样本的观测值为1.8，然后他来自男生的那个高斯分布，那么我们可以将这个样本表示为{1.8, 1, 0}。如果$z_{i1}$和$z_{i2}的值已知，也就是说每个人我已经标记为男生或者女生了，那么我们就可以利用上面说的最大似然算法来估计他们各自高斯分布的参数。但是它们未知，因此我们只能用EM算法。

$~~~~~~~~$咱们现在不是因为那个恶心的隐含变量（抽取得到的每个样本都不知道是从哪个分布抽取的）使得本来简单的可以求解的问题变复杂了，求解不了吗。那怎么办呢？人类解决问题的思路都是想能否把复杂的问题简单化。好，那么现在把这个复杂的问题逆回来，我假设已经知道这个隐含变量了，哎，那么求解那个分布的参数是不是很容易了，直接按上面说的最大似然估计就好了。那你就问我了，这个隐含变量是未知的，你怎么就来一个假设说已知呢？你这种假设是没有根据的。呵呵，我知道，所以我们可以先给这个给分布弄一个初始值，然后求这个隐含变量的期望，当成是这个隐含变量的已知值，那么现在就可以用最大似然求解那个分布的参数了吧，那假设这个参数比之前的那个随机的参数要好，它更能表达真实的分布，那么我们再通过这个参数确定的分布去求这个隐含变量的期望，然后再最大化，得到另一个更优的参数，……迭代，就能得到一个皆大欢喜的结果了。

$~~~~~~~~$这时候你就不服了，说你老迭代迭代的，你咋知道新的参数的估计就比原来的好啊？为什么这种方法行得通呢？有没有失效的时候呢？什么时候失效呢？用到这个方法需要注意什么问题呢？呵呵，一下子抛出那么多问题，搞得我适应不过来了，不过这证明了你有很好的搞研究的潜质啊。呵呵，其实这些问题就是数学家需要解决的问题。在数学上是可以稳当的证明的或者得出结论的。那咱们用数学来把上面的问题重新描述下。（在这里可以知道，不管多么复杂或者简单的物理世界的思想，都需要通过数学工具进行建模抽象才得以使用并发挥其强大的作用，而且，这里面蕴含的数学往往能带给你更多想象不到的东西，这就是数学的精妙所在啊）

四、EM算法推导

推导参考：
EM算法原理总结 —简洁清晰
EM算法（Expectation Maximization Algorithm）详解 – 后面的算法实现有一定的参考价值
机器学习之协方差矩阵、黑塞矩阵、标准差椭圆和EM算法 – 总结了jensen不等式实现原理，包括海森矩阵，正定等。

$~~~~~~~~$ 假设我们有一个样本集$\{x^{(1)},…,x^{(m)}\}$（身高），包含m个独立的样本。但样本i对应的类别$\{z^{(1)},…z^{(m)}\}$(如z1对应第一个x是男女)是未知的（相当于聚类），也即隐含变量。此时（x,z）即为完全数据。样本的模型参数为θ，则观察数据x的概率为$P(x|θ)$，完全数据的概率为$P(x,z|θ)$.

$~~~~~~~~$ 故我们需要估计概率模型$p(x,z)$的参数θ，但是由于里面包含隐含变量z，所以很难用最大似然求解，但如果z知道了，那我们就很容易求解了。

$~~~~~~~~$对于参数估计，我们本质上还是想获得一个使似然函数最大化的那个参数$θ$，现在与最大似然不同的只是似然函数式中多了一个未知的变量z，见下式（1）。也就是说我们的目标是找到适合的$θ$和$z$让$L(θ)$最大。那我们也许会想，你就是多了一个未知的变量而已啊，我也可以分别对未知的θ和z分别求偏导，再令其等于0，求解出来不也一样吗？

$$\begin{aligned} \hat θ ,\hat z &= \arg \max _{θ,z} L(θ,z) = \arg \max _{θ,z}\sum_{i=1}^m \ln \sum_{z^{(i)}}p(x^{(i)},z^{(i)};θ) -- (含有两个参数的似然函数)\\ &= \sum_{i=1}^m \ln \sum_{z^{(i)}}p(x^{(i)},z^{(i)};θ)&(1)\\ & = \sum_{i=1}^m \ln \sum_{z^{(i)}} Q_i(z^{(i)}) \frac {p(x^{(i)},z^{(i)};θ)}{ Q_i(z^{(i)}) }&(2) \\ & \geq \sum_{i=1}^m \sum_{z^{(i)}} Q_i(z^{(i)}) \ln \frac {p(x^{(i)},z^{(i)};θ)}{ Q_i(z^{(i)}) } &(3) \end{aligned}$$

$~~~~~~~~$ 其中 (2)式中引入Q， $Q_i(z^{(i)})$为新引入的一个未知分布，满足：

$$\sum_{z^{(i)}} Q_i(z^{(i)}) = 1 , 1 \geq Q_i(z^{(i)}) \geq 0$$
引入这个Q这个Q就可以看成 $\frac {p(x^{(i)},z^{(i)};θ)}{ Q_i(z^{(i)}) }$权重，这样整体就可以看成log(E(Y))了。
(3)式中引入Jensen不等式（对数函数为凸函数：这个是外国叫法，我国高中叫做凹函数）：
$$log (E(y)) \geq E(log(y))$$

$~~~~~~~~$ 本质上我们是需要最大化（1）式,，也就是似然函数，但是可以看到里面有“和的对数”，求导后形式会非常复杂，所以很难求解得到未知参数z和θ。那OK，我们可否对（1）式做一些改变呢？我们看（2）式，（2）式只是分子分母同乘以一个相等的函数，还是有“和的对数”啊，还是求解不了，那为什么要这么做呢？咱们先不管，看（3）式，发现（3）式变成了“对数的和”，那这样求导就容易了。我们注意点，还发现等号变成了不等号，为什么能这么变呢？这就是Jensen不等式的大显神威的地方。最后要求$L(θ)$最大，中有在不等式相等的时候才能取得最大的；根据Jensen不等式如果取到等于，就有$\frac {p(x^{(1)},z^{(1)};θ)}{ Q_i(z^{(1)}) } = \frac {p(x^{(2)},z^{(2)};θ)}{ Q_i(z^{(2)}) } =...=\frac {p(x^{(i)},z^{(i)};θ)}{ Q_i(z^{(i)}) }=C$ 为一个常数的时候等式成立（因为这个数i个都是相等的一个定值数）。

$~~~~~~~~$ 这个时候有：

$$\frac {p(x^{(i)},z^{(i)};θ)}{ Q_i(z^{(i)}) }=C \\ p(x^{(i)},z^{(i)};θ) = C * Q_i(z^{(i)}) \\ \sum p(x^{(i)},z^{(i)};θ) = C * \sum Q_i(z^{(i)})\\ 由\sum_{z^{(i)}} Q_i(z^{(i)}) = 1 \\ \sum p(x^{(i)},z^{(i)};θ) = C$$
重新再来看Q:

$$Q_i(z^{(i)}) = \frac {p(x^{(i)},z^{(i)};θ)}{C } = \frac{p(x^{(i)},z^{(i)};θ)}{ \sum p(x^{(i)},z^{(i)};θ) } = \frac{p(x^{(i)},z^{(i)} ;θ)}{ p(x^{(i)};θ) } = p(z^{(i)} ;x^{(i)},θ)$$
就是一个关于一致x,θ的隐含变量z分布。

Jensen不等式：

$~~~~~~~~$ 设f是定义域为实数的函数，如果对于所有的实数x。如果对于所有的实数x，f(x)的二次导数大于等于0，那么f是凸函数。当x是向量时，如果其hessian矩阵H是半正定的，那么f是凸函数。如果只大于0，不等于0，那么称f是严格凸函数。

Jensen不等式表述如下：
如果f是凸函数，X是随机变量，那么：E[f(X)]>=f(E[X])

特别地，如果f是严格凸函数，当且仅当X是常量时，上式取等号。

$~~~~~~~~$如果用图表示会很清晰：

图中，实线f是凸函数，X是随机变量，有0.5的概率是a，有0.5的概率是b。（就像掷硬币一样）。X的期望值就是a和b的中值了，图中可以看到E[f(X)]>=f(E[X])成立。

$~~~~~~~~$ 当f是（严格）凹函数当且仅当-f是（严格）凸函数。

$~~~~~~~~$Jensen不等式应用于凹函数时，不等号方向反向。

$~~~~~~~~$回到公式（2），因为f(x)=log x为凹函数（其二次导数为$-\frac{1}{x^2}<0$）。

（2）式中$\sum_{z^{(i)}} Q_i(z^{(i)})[ \frac {p(x^{(i)},z^{(i)};θ)}{ Q_i(z^{(i)}) }]$是$[ \frac {p(x^{(i)},z^{(i)};θ)}{ Q_i(z^{(i)}) }]$ 的期望(因为期望定义为：E(X)=∑x*p(x)，f(X)是X的函数，则E(f(X))=∑f(x)*p(x))，考虑到，又$\sum_{z^{(i)}} Q_i(z^{(i)}) = 1$，所以就可以得到公式（3）的不等式了：

$$\begin{aligned} & \sum_{i=1}^m \ln \sum_{z^{(i)}} Q_i(z^{(i)}) \frac {p(x^{(i)},z^{(i)};θ)}{ Q_i(z^{(i)}) } （式2） & \geq \sum_{i=1}^m \sum_{z^{(i)}} Q_i(z^{(i)}) \ln \frac {p(x^{(i)},z^{(i)};θ)}{ Q_i(z^{(i)}) } （式3） \end{aligned}$$
回到上面，现在已知 $Q_i(z^{(i)})= p(z^{(i)} ;x^{(i)},θ)$ 并且在这个条件下取得等号：
$$\begin{aligned} \hat θ ,\hat z &= \arg \max _{θ,z} L(θ,z) = \arg \max _{θ,z}\sum_{i=1}^m \ln \sum_{z^{(i)}}p(x^{(i)},z^{(i)};θ) -- (含有两个参数的似然函数)\\ & = \sum_{i=1}^m \sum_{z^{(i)}} Q_i(z^{(i)}) \ln \frac {p(x^{(i)},z^{(i)};θ)}{ Q_i(z^{(i)}) } & \end{aligned}$$
上面式子其中的一步求 $L$ 后存在两个隐含变量，这个时候呢先可以随意给一个θ通过这个θ值求使得上面式子最大化的 $Q_i(z^{(i)})$ 再通过 $Q_i(z^{(i)})$求新一轮的θ。这样通过几轮迭代就当最后趋于稳定时候就得到最终值 。这种先确定一个在逐步迭代的方法就是EM算法

EM算法（Expectation-maximization）：

$~~~~~~~~$期望最大算法是一种从不完全数据或有数据丢失的数据集（存在隐含变量）中求解概率模型参数的最大似然估计方法。

EM的算法流程：

初始化分布参数θ；

重复以下步骤直到收敛：

$~~~~~~~~$E步骤：根据参数初始值或上一次迭代的模型参数来计算出隐性变量的后验概率，其实就是隐性变量的期望。作为隐藏变量的现估计值：

$$Q_i(z^{(i)}) := p(z^{(i)} ;x^{(i)},θ)$$
$~~~~~~~~$ M步骤：将似然函数最大化以获得新的参数值：
$$θ : = \arg \max _{θ} \sum_{i=1}^m \sum_{z^{(i)}} Q_i(z^{(i)}) \log \frac {p(x^{(i)},z^{(i)};θ)}{ Q_i(z^{(i)}) }$$

这个不断的迭代，就可以得到使似然函数L(θ)最大化的参数θ了。那就得回答刚才的第二个问题了，它会收敛吗？

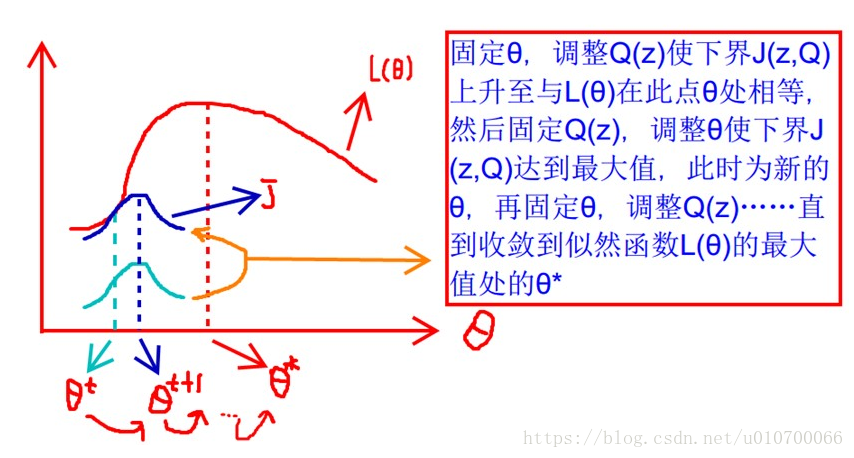
感性的说，因为下界不断提高，所以极大似然估计单调增加，那么最终我们会到达最大似然估计的最大值。理性分析的话，就会得到下面的东西：

总结：

EM算法只是里面的思想，其中很多计算都是求最大化似然函数变量的推导公式。比如里面的Jensen不等式。还有Q分布的转换。这些都是给出具体EM实现的可行性。
EM算法思想的核心就是在多个隐含变量的情况下可以先求其中一个，再求另外一个参数的方法。通过算法的收敛性进行逐步迭代求解。
最后，理解原理就好。不懂的话最好是一起推导一遍。就都可以了。