Expectation Maximisation (EM)

转眼三月也过了一周了，目前看来经过全国人民的无私奉献和医务工作者的辛勤付出，疫情得到了初步的控制。最近几天每天的新增确诊病例除武汉外已经几乎没有了，新增的也是输入型病例，而且武汉本身的每日新增数目也下降到了三四百左右，此外每天的治愈人数仍稳定保持在几千例，一切都在慢慢的变好。感谢广大投身于疫情防治工作的所有国人，无数人用身体力行的宣告着：苟利国家生死以，岂因祸福避趋之。

为了不给国家添麻烦，作为学生的我们也只能受困于家里而无法按时返校啦。到了这个阶段，实验做不成，实习找不了，还是很难受的，但想想自己这么菜，顿时也就这样啦。趁着这段时间一方面回顾总结下之前学习的东西，一方面紧跟领域最新动态，虽然效率有些降低，好在仍在坚持。这不是一个EM算法和高斯混合聚类断断续续就看了两三天，真难呀……[突然就扯远了]

EM算法也称期望最大化算法，它作为机器学习领域一个经典的算法广泛的应用机器学习和深度学习的各个具体的任务中。与其说它是一个具体的算法，不如说它提供了一种优秀的解决问题的思路，通过引入隐变量来迭代的解决本身无法直接求解的问题。

如何直观的理解EM算法的原理呢？很多的博文和资料都使用了概率统计中经典的道具-硬币。假设现有有两枚硬币 $A$ 和 $B$ ，其中 $A$ 向上的概率为 $\theta_A$ ， $B$ 向上的概率记为 $\theta_{B}$ 。如果现在我们随机的选择一枚进行投掷，此时具体选择的是哪一枚硬币是知道的，然后每轮投10次，总共投五轮，然后来计算参数 $\theta_A$ 和 $\theta_B$ 。投掷的具体情况如下所示：

由于每一次投掷时选择的硬币是可知的，因此我们只需要分别统计五轮结果中 $A$ 和 $B$ 具体的结果即可。从上图可以看出， $A$ 一共投了30次，其中24次向上，6次向下； $B$ 一共投了20次，其中向上9次，向下11次。那么我们可以很轻松的得到： $\hat{\theta_{A}}=\frac{24}{23+6}=0.80 \\ \hat{\theta_{B}}=\frac{9}{9+11}=0.45$
其中 $\hat{}$ 表示对于真实参数的估计。当实验的次数足够多时，根据大数定律可知，最后实验的结果就非常接近真实值。

但如果在每次选择硬币时并不知道具体是哪一枚，我们如何根据投掷的结果来估计 $\theta_A$ 和 $\theta_B$ 呢？此时我们在估计参数前还需要猜测投掷的硬币是 $A$ 还是 $B$ ，或者准确的说它是 $A$ 的概率是多大，或是 $B$ 的概率又是多少。这里的硬币选择概率就是所谓的隐变量，而解决这类问题就需要EM算法帮忙了。

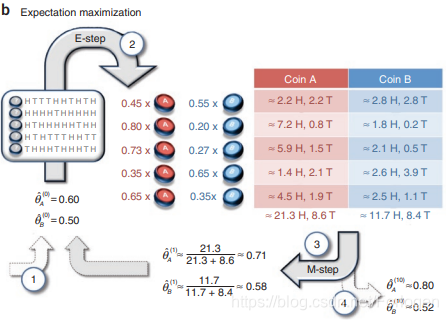
为了表述统一，下面直接用数字来表示具体的流程

假设 $\theta_A$ 和 $\theta_B$ 的估计值分别记为 $\hat{\theta_{A}^{(0)}}=0.60，\hat{\theta_{B}^{(0)}}=0.50$ ，其中上标表示第几次，然后依然进行投掷五轮得到上面的实验结果。其中第一轮结果为 $[H \ T \ T \ T \ H \ H \ T \ H \ T \ H]$ ，那么按照概率公式得硬币为 $A$ 的概率: $P(A)=\frac{\theta_{A}^5 \times(1 - \theta_{A})^5}{\theta_{A}^5 \times(1 - \theta_{A})^5 + \theta_{B}^5 \times(1 - \theta_{B})^5} = \frac{0.6^5 \times 0.4^5}{0.6^5 \times 0.4^5 + 0.5^5 \times 0.5^5}=0.45$
同理第一轮硬币为 $B$ 的概率 $P(B)=0.55$ 。最后依次计算每一轮的估计结果，如下所示：

	P（A）	P(B)
1	0.45	0.55
2	0.80	0.20
3	0.73	0.27
4	0.35	0.65
5	0.65	0.35

经过五轮的实验，我们对于每一轮 $\theta_A$ 和 $\theta_B$ 都有一个估计值，接下来求 $A$ 和 $B$ 正反面分别对应的期望。第一轮中，向上和向下分别有5次，得对应期望为2.25H和2.25H，同理可求出第一轮中为 $B$ 时向上和向下得期望，以及其他轮中得情况。最后可得第一次五轮投掷后得估计值： $\hat{\theta_{A}^{(1)}}=0.71 ，\hat{\theta_{B}^{(1)}}=0.58$
参数更新后重新进行五轮投掷，按照上面步骤同样得方法进行参数估计，10次后的结果为： $\hat{\theta_{A}^{(10)}}=0.82 ，\hat{\theta_{B}^{(10)}}=0.52$ 可以看出10次试验后的参数值和真实值已经很接近了
之后经过多次实验使得 $\theta_A$ 和 $\theta_B$ 收敛。

泛泛而言，之前在求解最大似然估计（MLE）问题中，假设数据集为 $X=\{x_{1},...x_{n}\}$ ，模型用 $\theta$ 参数化表示，那么利用似然估计来求解模型参数的表达式可写作： $\theta^*=\argmax_{\theta} \sum_{X}\log L(\theta|X)$
如果此时数据 $x_{i},i=1...,n$ 均采样自单个的高斯分布 $x \sim N(\mu,\Sigma)$ ，那么它所对应的似然函数为： $\begin{aligned} \log p(X) &=\sum_{i=1}^{N} \log \mathcal{N}\left(x_{i} | \mu, \Sigma\right) \\ &=\sum_{i=1}^{N} \log \frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{\left(z_{i}-\mu\right)^{3}}{2 \sigma^{2}}} \\ &=\sum_{i=1}^{N} \log \frac{1}{\sqrt{2 \pi} \sigma}+\sum_{i=1}^{N}-\frac{\left(x_{i}-\mu\right)^{2}}{2 \sigma^{2}} \\ &=-\frac{N}{2} \log 2 \pi-\frac{N}{2} \log \sigma^{2}-\frac{1}{2 \sigma^{2}} \sum_{i=1}^{N}\left(x_{i}-\mu\right)^{2} \end{aligned}$

然后使用似然函数分别对 $\mu$ 和 $\Sigma$ 求偏导并令偏导数为零可得：
$\begin{aligned} \frac{\partial \log p(X)}{\partial \mu} &=\frac{1}{\sigma^{2}} \sum_{i=1}^{N}\left(x_{i}-\mu\right)=0 \\ & \Rightarrow \mu=\frac{1}{N} \sum_{i=1}^{N} x_{i} \\ \frac{\partial \log p(X)}{\partial \sigma^{2}} &=-\frac{N}{2 \sigma^{2}}+\frac{1}{2 \sigma^{4}} \sum_{i=1}^{N}\left(x_{i}-\mu\right)^{2}=0 \\ & \Rightarrow \sigma^{2}=\frac{1}{N} \sum_{i=1}^{N}\left(x_{i}-\mu\right)^{2} \end{aligned}$

将 $X$ 中的数据导入第一个式子可得 $\mu$ ，再将两者代入后式的 $\sigma^2$ 。

而如果此时数据的分布并不能由单个的高斯分布合理采样获取的话，我们需要使用混合模型进行估计，即采用多个高斯分布的线性组合来估计数据所满足的真实分布。单个高斯分布中有 $p(x)= \mathcal{N}\left(x_{i} | \mu, \Sigma\right)$ ，混合模型中每个高斯分布都有着不同的参数 $\mu$ 和 $\Sigma$ ，另外单个数据点采样自某个具体的高斯分布的概率也是不同的，将其记为 $\pi_{k}$ ，其中 $k$ 表示混合模型中高斯分布的个数， $\pi_{k}$ 所满足的分布记为 $p(k)$ ，那么有： $p(x)=\sum_{k=1}^{K} \pi_{k} \mathcal{N}\left(x | \mu_{k}, \Sigma_{k}\right)$ 其中有 $\sum_{k=1}^K=1, 0 \leq \pi_{k} \leq 1$ 。

根据最前面硬币投掷的例子同理可知，此时 $x$ 采样就需要经过两步：首先需要从 $p(k)$ 中得到一个分布，然后从得到的分布中进行采样得到 $x_{i}$ ，那么它所对应的边缘概率分布为： $p(x)=\sum_{k=1}^K p(k)p(x|k)$ 即 $x_{i}$ 的采样受到 $p(k)$ 的制约。根据贝叶斯公式 $P(a|b)=\frac{p(b|a)p(a)}{p(b)}$ 得 $\pi_{k}$ 的后验概率分布为： $\begin{aligned} p(k | x) &=\frac{p(x | k) p(k)}{\sum_{l} p(x | l) p(l)} \\ &=\frac{\pi_{k} \mathcal{N}\left(x | \mu_{k}, \Sigma_{k}\right)}{\sum_{l} \pi_{l} \mathcal{N}\left(x | \mu_{l}, \Sigma_{l}\right)} \end{aligned}$
此时对数似然函数为： $\log p(X)=\sum_{i=1}^{N} \log \left\{\sum_{k=1}^{K} \pi_{k} \mathcal{N}\left(x_{i} | \mu_{k}, \Sigma_{k}\right)\right\}$
令 $\theta=(\mu,\Sigma,\pi)，\theta^* = (\mu^*,\Sigma^*,\pi^*)$ ，那么对于 $\theta^*$ 的极大似然估计为： $\begin{aligned} \theta^{*} &=\arg \max _{\theta} \sum_{i=1}^n \log P(x_{i} ; \theta) \\ &=\arg \max _{\theta} \sum_{i=1}^n \log \sum_{k=1}^K P(Z,\pi_{k}) P(x_{i}| k ; \mu, \Sigma) \\ &=\arg \max _{\theta} \sum_{i=1}^n \log \sum_{k=1}^K P(x_{i}, k; \theta) \end{aligned}$

而这样形式的式子是很难直接来通过求解析解的方式得到最终的参数估计的，这是EM算法思想就闪亮登场啦。

在正式的使用EM算法来解决上面的问题前，我们先回顾一些所需的基础知识：

凸函数： $f(x)$ 满足对定义域上任意的两个数 $a,b$ 有 $f(\frac{(a+b)}{2}) \geq \frac{f(a)+f(b)}{2}$

Jensen 不等式（琴生不等式）：如果 $f(x)$ 为凸函数，则有 $E[f(X)] \geq f(E[X])$ ，当且仅当 $x$ 是常量 $c$ 时等号成立

引入隐变量 $z_{i},i=1,...,k$ ，其中 $z_{i}$ 表示 $x_{i}$ 采样自第 $z_{i}$ 个分布，那么引入了隐变量后似然函数为： $\begin{aligned} \mathcal{L}(\theta ; X) &=\sum_{i=1}^{N} \log p\left(x_{i} | \theta\right) \\ &=\sum_{i=1}^{N} \log \sum_{z_{i}} p\left(x_{i}, z_{i} | \theta\right) \\ &=\sum_{i=1}^{N} \log \sum_{z_{i}} Q\left(z_{i}\right) \frac{p\left(x_{i}, z_{i} | \theta\right)}{Q\left(z_{i}\right)} \\ & \geq \sum_{i=1}^{N} \sum_{z_{i}} Q\left(z_{i}\right) \log \frac{p\left(x_{i}, z_{i} | \theta\right)}{Q\left(z_{i}\right)} \end{aligned}$ 其中 $Q(z_{i})$ 是关于 $z_{i}$ 的函数，根据概率的定义有 $\sum Q_{z_{i}}=1$ ，且有 $Q_i(z_i) = \frac{P(x_i,z_i;\theta)}{\sum\limits_{z}P(x_i,z_i;\theta)} = \frac{P(x_i,z_i;\theta)}{P(x_i;\theta)} = P( z_i|x_i;\theta))$ 此时 $Q(z_i)$ 为隐变量 $Z$ 的后验分布，似然函数取等号有 $\mathcal{L}\left(\theta^{(t)} ; X\right)=\sum_{i=1}^{N} \sum_{z_{i}} Q^{(t)}\left(z_{i}\right) \log \frac{p\left(x_{i}, z_{i} | \theta^{(t)}\right)}{Q^{(t)}\left(z_{i}\right)}$
然后对其进行求偏导并令偏导式为零来得到第 $t$ 次迭代的最优参数列表 $\theta^{(t+1)}=\underset{\theta}{\arg \max } \mathcal{L}(\theta ; X)$ 。这时第 $t+1$ 次迭代的似然函数为 $\mathcal{L}\left(\theta^{(t+1)} ; X\right)$ ，然后继续上述的过程不断迭代，直到收敛。

而证明迭代过程收敛只需要证明 $\mathcal{L}\left(\theta^{(t+1)} ; X\right) \geq \mathcal{L}\left(\theta^{(t)} ; X\right)$ 。
$\begin{aligned} \mathcal{L}\left(\theta^{(t+1)} ; X\right) &=\sum_{i=1}^{N} \log \sum_{z_{i}} Q^{(t)}\left(z_{i}\right) \frac{p\left(x_{i}, z_{i} | \theta^{(t+1)}\right)}{Q^{(t)}\left(z_{i}\right)} \\ & \geq \sum_{i=1}^{N} \sum_{z_{i}} Q^{(t)}\left(z_{i}\right) \log \frac{p\left(x_{i}, z_{i} | \theta^{(t+1)}\right)}{Q^{(t)}\left(z_{i}\right)} \\ & \geq \sum_{i=1}^{N} \sum_{z_{i}} Q^{(t)}\left(z_{i}\right) \log \frac{p\left(x_{i}, z_{i} | \theta^{(t)}\right)}{Q^{(t)}\left(z_{i}\right)} \\ &=\mathcal{L}\left(\theta^{(t)} ; X\right) \end{aligned}$

下面总结下EM算法求解的流程：

随机初始化模型参数 $\theta^0$ ，例如在混合高斯模型中常初始化为 $\theta^0=(\mu=0, \Sigma=1, \pi = 1/2)$

进行EM算法的迭代：
E步：计算联合分布的条件概率期望： $L\left(\theta, \theta^{t}\right)=\sum_{i=1}^{m} \sum_{z_i} Q_{i}\left(z_i\right) \log P\left(x_i, z_i ; \theta\right)$
M步：极大化似然函数得到 $\theta^{t+1}$ ： $\theta^{t+1}=\argmax L(\theta, \theta^t)$
如果此时收敛则算法结束，否则继续E步迭代直到收敛

EM算法实现代码：


# coding: utf-8

# # EM算法
# 
# # Expectation Maximization algorithm

import numpy as np
import math

pro_A, pro_B, por_C = 0.5, 0.5, 0.5

def pmf(i, pro_A, pro_B, por_C):
    pro_1 = pro_A * math.pow(pro_B, data[i]) * math.pow((1-pro_B), 1-data[i])
    pro_2 = pro_A * math.pow(pro_C, data[i]) * math.pow((1-pro_C), 1-data[i])
    return pro_1 / (pro_1 + pro_2)


class EM:
    def __init__(self, prob):
        self.pro_A, self.pro_B, self.pro_C = prob
        
    # e_step
    def pmf(self, i):
        pro_1 = self.pro_A * math.pow(self.pro_B, data[i]) * math.pow((1-self.pro_B), 1-data[i])
        pro_2 = (1 - self.pro_A) * math.pow(self.pro_C, data[i]) * math.pow((1-self.pro_C), 1-data[i])
        return pro_1 / (pro_1 + pro_2)
    
    # m_step
    def fit(self, data):
        count = len(data)
        print('init prob:{}, {}, {}'.format(self.pro_A, self.pro_B, self.pro_C))
        for d in range(count):
            _ = yield
            _pmf = [self.pmf(k) for k in range(count)]
            pro_A = 1/ count * sum(_pmf)
            pro_B = sum([_pmf[k]*data[k] for k in range(count)]) / sum([_pmf[k] for k in range(count)])
            pro_C = sum([(1-_pmf[k])*data[k] for k in range(count)]) / sum([(1-_pmf[k]) for k in range(count)])
            print('{}/{}  pro_a:{:.3f}, pro_b:{:.3f}, pro_c:{:.3f}'.format(d+1, count, pro_A, pro_B, pro_C))
            self.pro_A = pro_A
            self.pro_B = pro_B
            self.pro_C = pro_C
    

data=[1,1,0,1,0,0,1,0,1,1]

em = EM(prob=[0.5, 0.5, 0.5])
f = em.fit(data)
next(f)

# 第一次迭代
f.send(1)

# 第二次
f.send(2)

em = EM(prob=[0.4, 0.6, 0.7])
f2 = em.fit(data)
next(f2)

f2.send(1)

f2.send(2)

参考

EM算法原理总结

 Expectation Maximisation (EM)

What is the expectation maximization algorithm?

怎么通俗易懂地解释EM算法并且举个例子?

如何感性地理解EM算法？

EM算法学习(Expectation Maximization Algorithm)

EM-最大期望算法

 徐亦达机器学习：Expectation Maximization EM算法

Forlogen

发布了295 篇原创文章 · 获赞 103 · 访问量 20万+

私信关注

Expectation Maximisation (EM)

参考

猜你喜欢