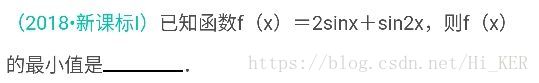数学基础--导数（例题讲解）

说明：以下内容主要是结合高中数学导数与信息学竞赛展开的，不是导数的入门教程，需要读者有一定的导数基础

从高考题说起

这道题对你来说是否很简单呢，请看下面的题：

（Hi_ker原创）（128M,1000ms）小凯的问题

参加了2018年高考的小凯很伤心，数学填空题第16题（如图）他没有做出来，所以他决定在暑假恶补导数，他想了Q个问题，都形如：已知函数 f(x)=k sinx + sin kx ,求f(x)的最小值，可他还是不会做，所以他找到了会编程的你。

输入：第一行Q,之后Q行每行一个值，表示k

输出：Q行，表示每道题的回答（保留三位小数）

样例输入：

样例输出：

-2.598

100%的数据满足Q<=100,1<=k<=1000且k为整数

解析：

我们先看2018全国卷一那道题，今年的填空最后一道比较水，熟悉导数的同学，应该5分钟之内可以解决吧

解： $f'(x)=2cos x+2cos2x$ ,考虑 $x\epsilon (0,\pi/2)$ ,

令 $f'(x)=0\rightarrow 2cosx+2(2cos^2x-1)=0\rightarrow cosx=1/2$

当 $cosx=1/2$ 时 $f(x)$ 有最大值，为： $\frac{3\sqrt{3}}{2}$ ,又该函数上界与下界相同，所以其最小值为： $-\frac{3\sqrt{3}}{2}$

如果你熟悉琴生不等式，这道题可以秒解：

因为 $sinx$ 在 $x\epsilon (0,\pi/2)$ 为凸函数，又 $f(x)=sinx+sinx+sin(\pi-2x)$

由琴生不等式 $\frac{sinx+sinx+sin(\pi-2x)}{3} \leqslant sin(\frac{x+x+\pi-2x}{3})=sin\frac{\pi}{3}$

所以目标最大值为 $3sin\tfrac{\pi}{3}=\tfrac{3\sqrt{3}}{2}$ ,所以目标最小值为 $-\tfrac{3\sqrt{3}}{2}$

好，下面我们来看小凯的问题：

我们先求最大值，最大值的相反数就是最小值

这显然就是一个求函数极值的题，只不过k不确定，我们先不考虑二分，三分等方法，来数学推导一番：

我们先求目标函数的最大值区间，显然这个区间应该在 $(0,\pi)$ （想想为什么）

然后求导： $f'(x)=kcosx+kcoskx$

令： $f'(x)=0\rightarrow kcosx+kcoskx=0\rightarrow cosx+coskx=0$

然后用和差化积公式： $2cos\tfrac{kx+x}{2}cos\tfrac{kx-x}{2}=0$

现在问题来了，当x在区间 $(0,\pi)$ 取多少时函数取最大值呢？

如果我们把 $f(x)$ 图像对应k不同时分别画出来:

我们会发现，随着k的增大，g(x)的图像越来越显得波动，把两个函数叠加，我们会发现这个函数越来越不稳定,所以面对这道题最暴力的解法就是把区间细分到满足精度的小区间，依次枚举求最值。

但是你会发现这些函数长落是交替的，每一个极值点都对应其一阶导数为0的情况，我们可以考虑枚举使一阶导为0的x的值，即: $cos\tfrac{kx+x}{2}=cos(\tfrac{\pi}{2}+K\pi)\rightarrow x=\tfrac{(2K+1)\pi}{k+1}$ 或： $cos\tfrac{kx-x}{2}=cos(\tfrac{\pi}{2}+K\pi)\rightarrow x=\tfrac{(2K+1)\pi}{k-1}$ 其中 $K\epsilon N$

这样枚举量就小了很多

具体细节参见代码：

#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
const double PI=3.14159256;
int Q,k;
int main(){
	scanf("%d",&Q);
	while(Q--){
		scanf("%d",&k);
		double ans=0;
		for(int K=0;2*K<k;K++){//根据x范围求K的范围 
			double x=PI*(2*K+1)/(k+1);
			ans=max(ans,sin(x)*k+sin(k*x));
		}
		for(int K=0;2*K+2<k;K++){//k=1不需要特判，想想为什么 
			double x=PI*(2*K+1)/(k-1);
			ans=max(ans,sin(x)*k+sin(k*x));
		}
		printf("%.3lf\n",-ans);//注意是求最小值 
	}
	return 0;
}

建议大家有时间去看看琴生不等式，并思考，这道题是否可以用琴生不等式解决