人工智能数学基础知识复习（一）——导数、偏导数、方向导数、梯度

从事AI行业最重要的知识莫过于数学了，或者说对于计算机领域乃至工科领域都是很重要的。最近觉得数学知识有点遗忘，遂在网易云课堂购买了唐宇迪老师的《数据科学人工智能-必备数学基础》课程学习，这里把课程笔记和大家分享一下，供需要的朋友参考。

唐老师网易云课堂课程传送门https://study.163.com/course/courseMain.htm?courseId=1005695008，CSDN学院课程传送门https://edu.csdn.net/course/detail/8850。这门课是需要付费购买的，我不是什么托儿，只是分享自己的学习心得。唐老师的课一搬适合快速复习知识或者入门一种技术，想要深入学习一方面靠自己多思考练习，另一方面可以跟着国内外大牛的免费公开课学习。

废话不多说，下面步入正题。

一、导数

在物理学中有平均速度和瞬时速度之说。平均速度有

$v=\frac{s}{t}$

其中 $v$ 表示平均速度， $s$ 表示路程， $t$ 表示时间。这个公式可以改写为

$\bar{v}=\frac{\Delta s}{\Delta t}=\frac{s(t_{0}{+\Delta t})-s(t_{0})}{\Delta t}$

其中 $\Delta s$ 表示两点之间的路程，而 $\Delta t$ 表示走过这段路程需要花费的时间。当 $\Delta t$ 趋向于0（ $\Delta t\rightarrow 0$ ）时，也就是时间变得很短时，平均速度也就变成了在 $t_{0}$ 时刻的瞬时速度，表示成如下形式：

$v(t_{0})=\lim_{\Delta t\rightarrow 0}\bar{v}=\lim_{\Delta t\rightarrow 0}\frac{\Delta s}{\Delta t}=\lim_{\Delta t\rightarrow 0}\frac{s(t_{0}+\Delta t)-s(t_{0})}{\Delta t}$

实际上上式表示的是路程 $s$ 关于时间 $t$ 的函数在 $t=t_{0}$ 处的导数。一般地，这样定义导数：如果平均变化率的极限存在，即有

$\lim_{\Delta x\rightarrow 0}\frac{\Delta y}{\Delta x}=\lim_{\Delta x\rightarrow 0}\frac{f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}$

则称此极限为函数 $y=f(x)$ 在点 $x_{0}$ 处的导数。记作 ${f}'(x_{0})$ 或 ${y}'|_{x=x_{0}}$ 或 $\frac{dy}{dx}|_{x=x_{0}}$ 或 $\frac{df(x)}{dx}|_{x=x_{0}}$ 。

通俗地说，导数就是曲线在某一点切线的斜率。

二、偏导数

设函数 $z=f(x,y)$ 在点 $(x_{0}, y_{0})$ 的邻域内有定义，当 $y=y_{0}$ ， $z$ 可以看做关于 $x$ 的一元函数 $f(x,y_{0})$ ，若该一元函数在 $x=x_{0}$ 处可导，即有

$\lim_{\Delta x\rightarrow0 }\frac{f(x_{0}+\Delta x, y_{0})-f(x_{0}, y_{0})}{\Delta x}=A$

函数的极限 $A$ 存在。那么称 $A$ 为函数 $z=f(x, y)$ 在点 $(x_{0}, y_{0})$ 处关于自变量 $x$ 的偏导数，记作 $f_{x}(x_{0}, y_{0})$ 或 $\frac{\partial z}{\partial x}|_{y=y_{0}}^{x=x_{0}}$ 或 $\frac{\partial f}{\partial x}|_{y=y_{0}}^{x=x_{0}}$ 或 $z_{x}|_{y=y_{0}}^{x=x_{0}}$ 。

偏导数在求解时可以将另外一个变量看做常数，利用普通的求导数方法求解，比如 $z=3x^{2}+xy$ 关于 $x$ 的偏导数就为 $z_{x}=6x+y$ ，这个时候y相当于x的系数。

某点 $(x_{0}, y_{0})$ 处的偏导数的几何意义为曲面 $z=f(x, y)$ 与面 $x=x_{0}$ 或面 $y=y_{0}$ 交线在 $y=y_{0}$ 或 $x=x_{0}$ 处切线的斜率。

三、方向导数

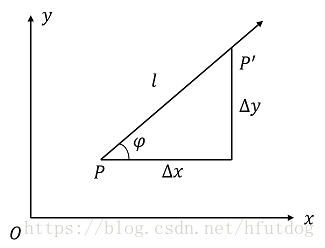
如图所示：

现有函数 $z=f(x,y)$ ，函数图像上有两点 $P$ 和 ${P}'$ ， $P$ 点和 ${P}'$ 两点横纵坐标的差值分别为 $\Delta x$ 和 $\Delta y$ ，那么函数在这两点之间的增量为 $\Delta z=f(x+\Delta x, y+\Delta y)-f(x,y)$ ，这两点之间的距离为 $|P{P}'|=\rho =\sqrt{(\Delta x)^{2}+(\Delta y)^{2}}$ 。如果函数的增量与这两点之间的距离成比例，那么这个比例就被称作在 $P$ 点沿着方向 $L$ 的方向导数，也即如下形式：

$\frac{\partial f}{\partial l}=\lim_{\rho \rightarrow 0}\frac{f(x+\Delta x, y+\Delta y)-f(x, y)}{\rho }$

简单地说，方向导数就是函数沿着某个方向的变化率。

四、梯度

在空间中，一个函数在一个点可以有任意方向，如果沿这些方向导数都存在，那么其中一定会有最大的一个，那么沿这个方向的方向导数也就是梯度。或者说，方向导数中最大值的方向就是梯度的方向，方向导数的最大值就是梯度的值。

那么在函数上某点任意方向的方向导数都存在的前提条件是什么呢？答案是函数在该点是可微的。比如说函数 $z=f(x,y)$ 在点 $P(x,y)$ 是可微的，那么该点沿任意方向 $l$ 的方向导数可以表示为：

$\frac{\partial f}{\partial l}=\frac{\partial f}{\partial x}\cos \varphi +\frac{\partial f}{\partial y}\sin \varphi$

其中， $\varphi$ 为 $x$ 轴和 $l$ 方向之间的夹角。

下面让我们看一下为什么说梯度是方向导数的最大值。

首先，梯度的具体定义为：函数 $z=f(x,y)$ 在平面域内具有连续的一阶偏导数，对于其中每一个点 $P(x, y)$ 都有向量 $^{\frac{\partial f}{\partial x}}\vec{i}+^{\frac{\partial f}{\partial y}}\vec{j}$ ，则将其称为函数在点 $P$ 的梯度，写作：

$gradf(x, y)=^{\frac{\partial f}{\partial x}}\vec{i}+^{\frac{\partial f}{\partial y}}\vec{j}$

已知 $\vec{e}=\cos \varphi \vec{i}+\sin \varphi \vec{j}$ 是方向 $l$ 上的单位向量，那么有

$\frac{\partial f}{\partial l}=\frac{\partial f}{\partial x}\cos \varphi +\frac{\partial f}{\partial y}\sin \varphi =(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y})\cdot (\cos \varphi ,\sin \varphi )$

$=gradf(x,y)\cdot \vec{e}=|gradf(x,y)|\cos \theta$

其中 $\theta =(gradf(x,y),\vec{e})$ ，也就是梯度方向和方向导数方向 $l$ 的夹角。

由上式可以得知，方向导数可以转换为梯度与其单位向量的点积，也就是梯度的模与梯度和方向导数之间夹角的乘积。而当 $\cos \theta=1$ 时，梯度的值等于方向导数的值，也就是方向导数取最大值的情况。

这里顺便提一下机器学习中常说的梯度下降，由于梯度的方向是与方向导数的最大值方向（向上增长的方向）一致的，所以梯度下降实际是沿着梯度的反方向进行的，采用梯度下降的意义在于使模型始终沿着使函数值最快减小的方向去优化，而这个函数便是损失函数loss。而且梯度在优化过程中并不是一成不变的，随着函数上点的移动，也就是优化过程的进行，方向导数时刻在变化，梯度也就时刻在变化，需要不断的调整梯度来完善模型。