一、模型表示
1.一些术语
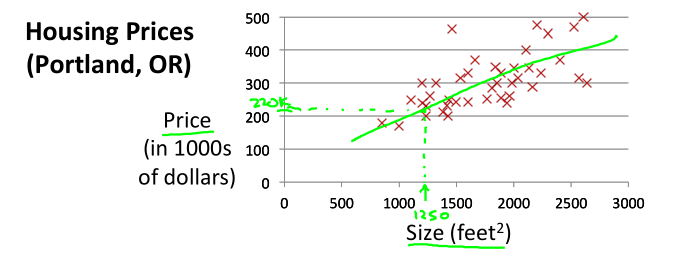
如下图,房价预测。训练集给出了房屋面积和价格,下面介绍一些术语:
x:输入变量或输入特征(input variable/features)。
y:输出变量或目标变量(output variable/target variable)。
(x, y):一个训练样本
(x(i), y(i)):第i个训练样本
m:样本数目

2.机器学习的一般过程
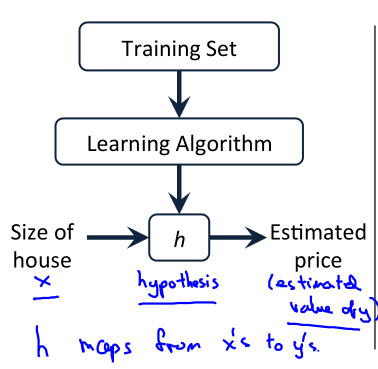
如图,机器学习算法通过学习训练集得出假设函数h(Hypothesis),然后接受输入x,输出y。假设函数h称为模型。
3.线性回归问题的假设函数
通过观察,我们使用的房价预测数据近似一条直线,所以我们将假设函数设为 h(x) = θ0 + θ1x,我们的目标是尽可能得使直线与训练集数据拟合。现阶段我们通过观察来假设函数模型,以后我们可以直接假设一个较为复杂的函数,然后通过正则化避免过拟合问题,这部分之后会讲。
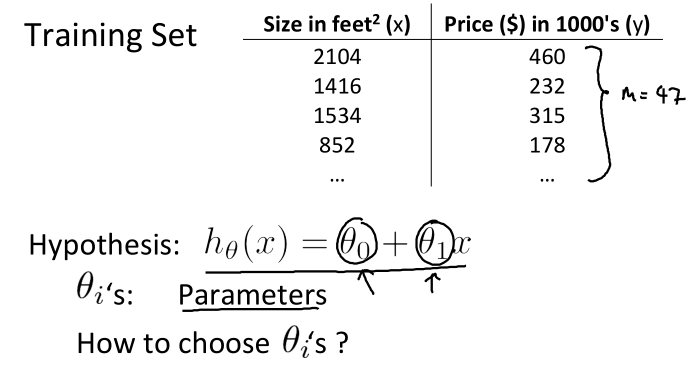
综上,我们得到假设函数:h(x) = θ0 + θ1x。这样问题就转变为求解θ0和θ1,使得曲线(或直线)h(x) 拟合训练数据。
二、代价函数(Cost Function)
1.代价函数推导与表示
从我们的目标出发,我们的目标是使曲线h(x) 拟合训练数据。从这点我们可以看出应该让训练数据尽可能的通过h(x)或离h(x)接近,故我们让y和h(x)的距离尽可能小,可以用减法运算来表示距离d,由于d有可能小于0,会使得代价函数J(θ0, θ1)反而变小,而实际上h(x)与y还是有距离的,故使用d2来表示。其中(x, y)为某一样本。
d2 = [h(x) - y]2
这样,我们将所有的样本所求出的预测值h(x)与y相减得到d,然后对所有的d求和就得到预测值与所有样本的距离的和,记为J(θ0, θ1),如下:
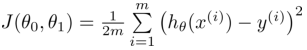
该公式称为h(x)的代价函数(Cost Function),又称平方误差函数(Squared Error Function)。上述公式是距离的平方再求和,这和相减的效果是一样的,样本数量为m,前面乘以1/m求平均值,分母的2主要是为了便于之后求导约掉。为使h(x)与y尽可能的接近,函数J(θ0, θ1)应尽可能小,故目标转变为求出使得函数J(θ0, θ1)尽可能小的θ0和θ1。即
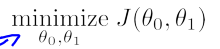
2.理解代价函数
为简化问题,我们将θ0置为0,这样,h(x) = θ1x,J也变为J(θ1)

观察下图,当θ1的值变化时,J(θ1)也跟着变化,可以观察到,当θ1= 0时h(x)与训练数据拟合的最好时,J(θ1)达到最小值。

从上面我们可以观察到函数J(θ1)为凸函数,并且对于线性回归问题,该函数只存在全局最小值,不存在局部最小值。这样,我们可以利用导数来求解极小值,同时也是最小值。
对于J(θ0, θ1)和J(θ1)同理,在绘制θ0与J(θ0, θ1)的关系时只需将θ1视为不变即可,并且求导时变为分别求J(θ0, θ1)对θ0和θ1的偏导数。
综上,我们明白了为使h(x)与训练数据拟合,必须求出使得J(θ0, θ1)最小的θ0和θ1,还知道了J(θ0, θ1)是凸函数,可以通过求导来求出最小值和对应的θ0和θ1。
三、梯度下降算法(Gradient Descent)
1.公式
上一节我们讲了可以使用导数的方式来求解θ0和θ1,本节的梯度下降算法利用的便是这种思想,其算法如下:

上述公式中α为学习率,该参数可以控制θ的变化速率。值得注意的是,在更新多个θ时要同步更新,不能先更新任意一个。
2.理解
上述公式初看可能难以理解,我们依旧使用简化的假设函数h(x) = θ1x和J(θ1)来解释。
如下图,当θ1位于极小值的右方时,J(θ1)单调增加,故![]() 大于0,这表明函数θ1正位于最小值的右方,要达到最小值应该要减小θ1,应该减去一个正数。故下面的公式会使得θ1接近最小值:
大于0,这表明函数θ1正位于最小值的右方,要达到最小值应该要减小θ1,应该减去一个正数。故下面的公式会使得θ1接近最小值:
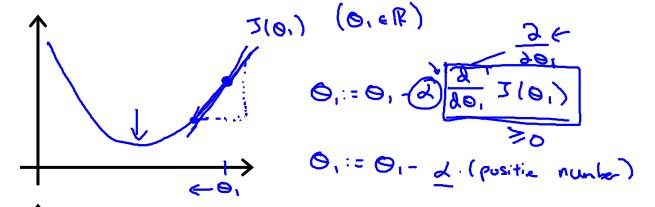
同理,当θ1位于极小值的左方时,J(θ1)单调减少故![]() 小于0,这表明函数θ1正位于最小值的左方要达到最小值应该要增加θ1,应该加上一个正数,即减去一个负数。故下面的公式会使得θ1接近最小值:
小于0,这表明函数θ1正位于最小值的左方要达到最小值应该要增加θ1,应该加上一个正数,即减去一个负数。故下面的公式会使得θ1接近最小值:
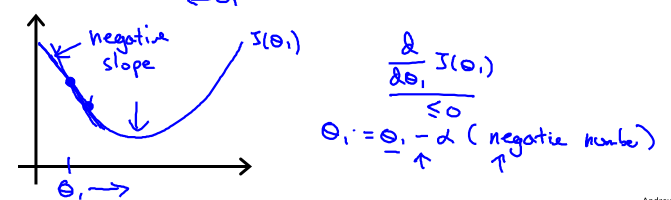
3.学习率α
对于J(θ1),我们求解θ1的公式是
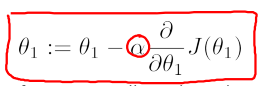
可以看到,若学习率α很小,那么θ1会很缓慢地减小;若学习率α很大,那么θ1变化会很大,甚至于越过了J(θ1)最小值对应的θ1,其在图像上表现为反复横跳,最终甚至无法收敛到最小值。如下图所示:
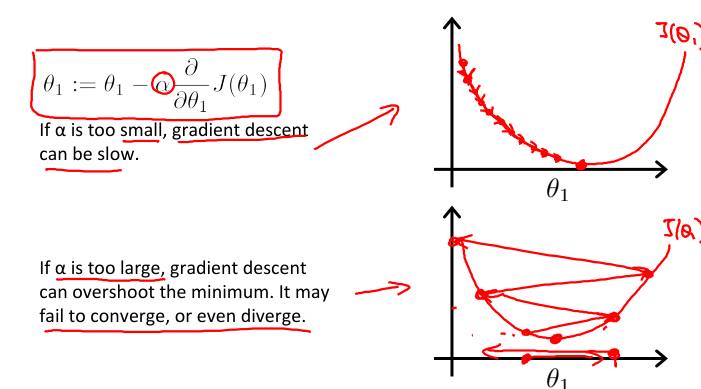
再思考,在上述求解θ1的公式中,我们是否需要在运行过程中定期修改α的值?
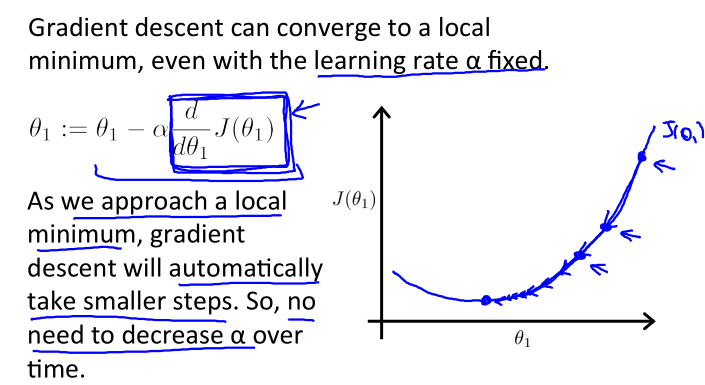
答案是不用。由于公式中的导数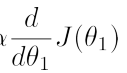 越接近极小值(同时是最小值)时会越来越小,对应到图像上表现为越来越平缓,所以
越接近极小值(同时是最小值)时会越来越小,对应到图像上表现为越来越平缓,所以 会越来越小,故θ1的变化越来越慢,直至收敛到使J(θ1)取得最小值。
会越来越小,故θ1的变化越来越慢,直至收敛到使J(θ1)取得最小值。
四、单变量线性回归问题求解
综合上述所有知识,我们得到如下总结:

我们首先假设了假设函数h(x) = θ0 + θ1x,然后为了求解θ0 和 θ1,我们从使得h(x) 拟合训练数据的想法出发,想到要使h(x) 与训练数据拟合,必须使得预测值h(x)与y的距离尽可能接近,故得到函数J(θ0 , θ1),问题转变为了求出使得最小化J(θ0 , θ1)对应的θ0 和 θ1,再从函数J(θ0 , θ1)为凸函数的特点出发,想到其在不同位置的导数正负不同,得到梯度下降算法。这样便可以使用梯度下降算法求得θ0 和 θ1,从而得到h(x)。现在问题只剩下一个,那就是求解![]() ,结合J(θ0 , θ1)的表达式求导,可以得到
,结合J(θ0 , θ1)的表达式求导,可以得到

这样,我们便求解了单变量线性回归问题,得到了拟合了数据的假设函数h(x)。
上述的梯度下降算法称为批量梯度下降(Batch Gradient Descent),所谓批量指的是在每一次梯度下降的过程中都使用了全部样本。