题目:
Sigma Function
Time Limit:2000MS Memory Limit:32768KB 64bit IO Format:%lld & %llu
Submit Status Practice LightOJ 1336
Description
Sigma function is an interesting function in Number Theory. It is denoted by the Greek letter Sigma (σ). This function actually denotes the sum of all divisors of a number. For example σ(24) = 1+2+3+4+6+8+12+24=60. Sigma of small numbers is easy to find but for large numbers it is very difficult to find in a straight forward way. But mathematicians have discovered a formula to find sigma. If the prime power decomposition of an integer is

Then we can write,
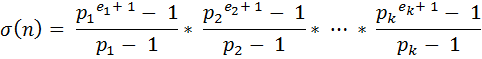
For some n the value of σ(n) is odd and for others it is even. Given a value n, you will have to find how many integers from 1 to n have even value of σ.
Input
Input starts with an integer T (≤ 100), denoting the number of test cases.
Each case starts with a line containing an integer n (1 ≤ n ≤ 1012).
Output
For each case, print the case number and the result.
Sample Input
4
3
10
100
1000
Sample Output
Case 1: 1
Case 2: 5
Case 3: 83
Case 4: 947
首先给出题目中的公式的推导过程:
n是一个整数,f(n)代表他的因子的和。假设n=12,对他进行素因子分解可得n=2^2*3。12的因子有1,2,3,4,6,12,和为28。根据题目中的公式:f(n)=(2^3-1)/(2-1)*(3^2-1)/(3-1)=7*4=28。为什么会是这样呢?将因子再进行素因子分解可以发现:1=2^0*3^0 , 2=2^1*3^0 , 3=2^0*3^1 , 4=2^2*3^0 , 6=2^1 *3^1 , 12=2^2*3^1。所以1+2+3+4+6+12=2^0*3^0+2^1*3^0+2^0*3^1+2^2*3^0+2^1 *3^1+2^2*3^1=(2^0+2^1+2^2)*(3^0+3^1)。利用等比数列前n项和公式:(2^3-1)/(2-1)*(3^2-1)/(3-1)=7*4=28。推导完毕。
事实上,这称之为积性函数。
解题思路:
题意:
求 1—n 中,有多少个数的因子和是偶数。
题解:
打表找规律。
素因子分解打表计算前n项和判断奇数偶数可以发现如下规律:
只要是2^x,a^2,2*a^2...只有这种数的因子和是奇数。所以,我们直接去重即可。
但是这些直接去重我们会发现减去的这些值有重复的,所以我们要判断下。
i (代表x||a): 0 1 2 3 4 5 6 7 8 9 ......
2^x: 1 2 4 8 16 32 64 128 ......
a^2: 0 1 4 9 16 25 36 49 64 ......
2*a^2: 0 2 8 18 32 50 72 ......
我们可以发现2^x里面有的数,a^2和2*a^2里面都有。
加下划线的字一一对应,加粗的字一一对应。
①2^x和a^2, 当x为偶数时二者出现重复。
②2^x和2*a^2,当x为奇数时,二者出现重复。
所以不需要考虑2^x的个数,直接用n减去a^2和2*a^2的个数就是我们要的结果。
易知:a^2的个数=sqrt(n),2*a^2的个数=sqrt(n/2)。
那么为什么会是这样呢?给出推导过程:
n=p1^e1*p2^e2...,则f(n)=(p1^(e1+1)-1)/(p1-1))*(p2^(e2+1)-1)/(p2-1))....
且(p1^(e1+1)-1)/(p1-1))=p1^0+p1^1......+p1^e1;
要使得f(n)为奇数,则(p1^(e1+1)-1)/(p1-1)到(pn^(en+1)-1)/(pn-1)都要为奇数;
因为奇数*奇数=奇数,奇数*偶数=偶数;
1)当p=2时,2^(e+1)-1,一定为奇数;
2)当p!=2时,则p为奇数(因为p是素因子),则当e为偶数时(p^(e+1)-1)/(p-1)为奇数。
经转化我们可以发现,2^6=8^2,2^11=2*32^2。也就是平方数和2倍的平方数。
则需要统计1到n中的平方数个数和2倍的平方数的个数,得到的为1到n中f(n)为奇数的个数。
#include <iostream>
#include <cmath>
#include <cstdio>
using namespace std;
typedef long long ll;
int main()
{
int t,cas=1;
cin>>t;
while(t--)
{
ll n,a,b;
cin>>n;
a=sqrt(n);
b=sqrt(n/2);
printf("Case %d: %lld\n",cas++,n-a-b);
}
return 0;
}用了唯一分解定理超时;
#include <iostream>
#include <stdio.h>
#include <string.h>
#define MAXN 1000006
#define LL long long
using namespace std;
bool isprime[MAXN+1];
int prime[MAXN/10], tot; //防止MLE
void getPrime() {
memset(isprime, true, sizeof(isprime));
isprime[0] = isprime[1] = false;
tot = 0;
for(int i = 2; i < MAXN; i++) {
if(isprime[i]) prime[tot++] = i;
for(int j = 0; j < tot && prime[j] <= MAXN / i; j++) {
isprime[i * prime[j]]=false;
if(i % prime[j] == 0) break;
}
}
}
LL ans,p;
int cnt;
bool getFactors(LL n) {
for(int i = 0; i < tot && prime[i] <= n / prime[i]; i++) {
if(n<prime[i])break;
cnt=0;
if(n % prime[i] == 0) {
while(n % prime[i] == 0) {
cnt++;
n /= prime[i];
}
if(prime[i]&1)
{
if(cnt&1)
return true;
}
}
}
if(n != 1&&n&1)
return true;
return false ;
}
int main()
{
getPrime() ;
int t;
LL n;
int Case=0;
scanf("%d",&t);
while(t--)
{
scanf("%lld",&n);
LL num=0;
for(LL i=1;i<=n;i++)
{
if(getFactors(i))
num++;
}
printf("Case %d: %lld\n",++Case,num);
}
return 0;
}