R语言与多元线性回归方程及各种检验
文章目录
一、模型建立
数据放在最后,自取试建立y与x1,x2,x3,x4,x5的线性回归方程
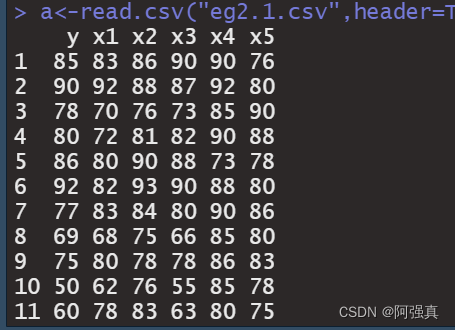
代码如下:
a<-read.csv("eg2.1.csv",header=T);a
b<-lm(y~x1+x2+x3+x4+x5,data=a)
这里介绍一个包,可以把结果用表格显示:
install.packages("flextable")
library(flextable)#制作表格
as_flextable(b)
输出结果如下:
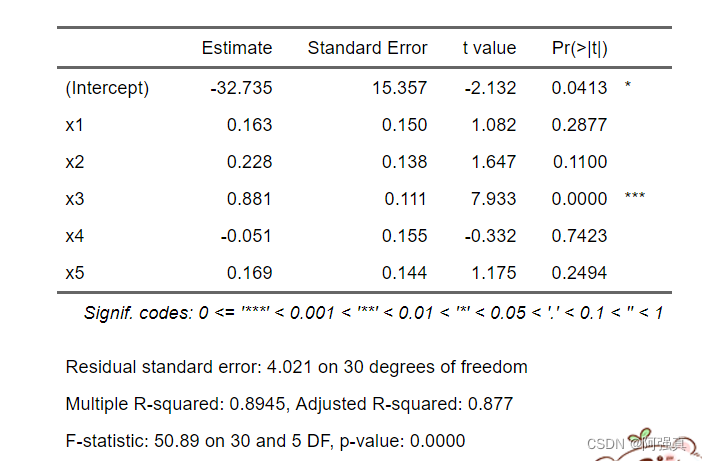
得到回归方程
y = − 32 + 0.163 x 1 + 0.228 x 2 + 0.881 x 3 − 0.05 x 4 + 0.169 x 5 y=-32+0.163x_1+0.228x_2+0.881x_3-0.05x_4+0.169x_5 y=−32+0.163x1+0.228x2+0.881x3−0.05x4+0.169x5
二、多重共线性
(1)产生的背景:
1.经济变量间具有共同变化的趋势。例如,对于时间序列数据收入、消费、就业率等等,在经济上升时期均呈现增长的趋势,而在经济收缩期,又都呈现下降趋势。当这些变量同时作为解释变量进入模型时就会带来多重共线性问题。
2.模型中引入了滞后变量,变量X常常与滞后变量高度相关
3.利用截面数据建立模型也可能会出现多重共线性。利用截面数据建模时,许多变量变化与发展规模有关,会出现同步增长的趋势,如资本、劳动力、科技、能源等投入与产出的规模相关,这时容易产生多重共线性。
4.样本数据自身的原因。例如,抽样仅仅限于总体中解释变量取值的一个有限范围,使得变量间变异不大;或由于总体受限,多个解释变量的样本数据相关,这时都可能出现多重共线性。
(2)多重共线性的检验
1.简单相关系数法:
一般而言,如果每两个解释变量的简单的相关系数(0阶自相关系数)比较高,如大于0.8,则可认为存在严重的多重共线性。
ab<-a[,c(2:6)]#只保留解释变量
corr<-cor(ab);corr
corrplot(corr,method="number",type="full",mar=c(0,0,0,0) ,bg="black",tl.col = "blue")
其中corrplot函数详细见这篇文章:
相关系数热力图
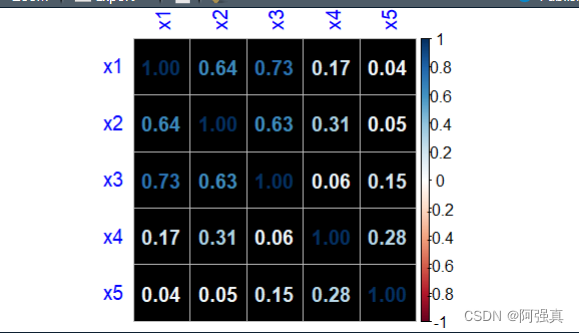
由上图可知,x1和x3的相关系数为0.73,初步判断不存在多重共线性。
2.方差膨胀因子(vif)法
一般vif大于10即可认为存在严重的多重共线性:
通过建立x1~x2+x3+x4+x5的线性关系得到R方,那么x1的方差膨胀因子就是
V I F = 1 1 − R 2 VIF=\frac{1}{1-R^2} VIF=1−R21
其他的类似,r语言有vif这个函数可以直接求:
library(car)#检验多重共线性的包
vif(b)#b是线性回归的结果

可以看出:vif值都小于10,即可判断出没有多重共线性
3.矩阵 X T X X^TX XTX的条件数k
条件数的定义为:
k ( X T X ) = ∥ X T X ∥ ⋅ ∥ ( X T X ) − 1 ∥ = λ max ( X T X ) λ min ( X T X ) \,\,k\left( X^TX \right) =\left\| X^TX \right\| \cdot \left\| \left( X^TX \right) ^{-1} \right\| =\frac{\lambda _{\max \left( X^TX \right)}}{\lambda \min \left( X^TX \right)} k(XTX)=∥∥XTX∥∥⋅∥∥∥(XTX)−1∥∥∥=λmin(XTX)λmax(XTX)
若k<100,则认为多重共线性的程度很小,在100到1000之间则认为存在中度或较强的多重共线性,若大于1000,则认为存在严重的多重共线性。
在R软件中,用kappa()计算矩阵的条件数,其使用方法为:
其中z是矩阵,exact=F即不精确计算条件数,近似计算
XX<-cor(ab)#先做出相关系数矩阵
kappa(XX)#对相关系数矩阵做
eigen(XX)#求特征值和特征向量
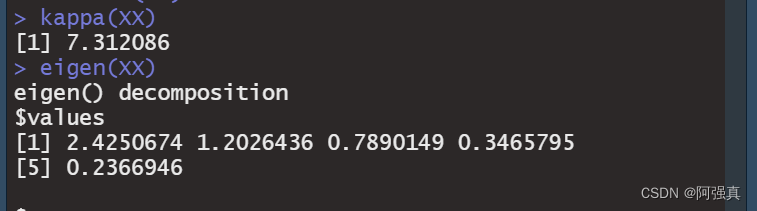
可以看出条件数的值为7,即不存在多重共线性。
(3)多重共线性的修正
本文虽然没有出现多重共线性的问题,但是如果出现了,该如何解决呢?
本文主要通过逐步回归来修正多重共线性
代码如下:
aaa<-step(b)
as_flextable(aaa)
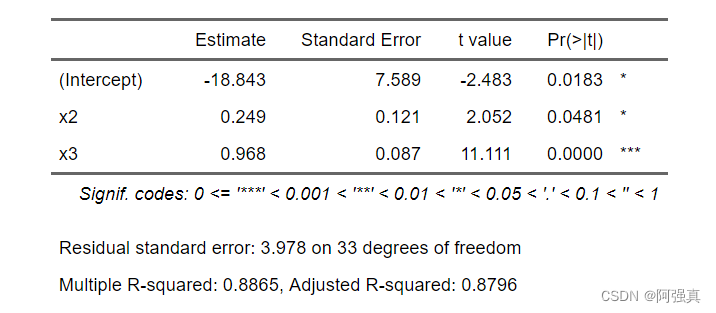
得到最后的回归方程:
y = − 18.43 + 0.249 x 2 + 0.986 x 3 y=-18.43+0.249x_2+0.986x_3 y=−18.43+0.249x2+0.986x3
二、异方差性的检验及修正
1.异方差性的实质
设模型为
Y i = β 0 + β 1 x 1 i + β 2 x 2 i + . . . + β k x k i + u i ( i = 1 , 2 , . . . n ) \\ Y_i=\beta _0+\beta _1x_{1i}+\beta _2x_{2i}+...+\beta _kx_{_{ki}}+u_i\left( i=1,2,...n \right) Yi=β0+β1x1i+β2x2i+...+βkxki+ui(i=1,2,...n)
如果其他假定均不变,但模型中随机误差项 u i u_i ui的方差为
V a r ( u i ) = σ i 2 ( i = 1 , 2 , . . . n ) Var(u_i)=\sigma_i^2(i=1,2,...n) Var(ui)=σi2(i=1,2,...n)
则称 u i u_i ui具有异方差性(heteroscedasiticity)
2.异方差性的检验
1.图示检验法
一般把标准化残差的绝对值大于等于2的观测值认为是可疑点,而把标准化残差值绝对值大于等于3认为是异常值
rst <- rstandard(b)#标准化残差
fit<-predict(b)#预测值
library(ggplot2)#载入ggplot2包
mn<-data.frame(rst,fit)
ggplot(mn,aes(fit,rst))+geom_point()
通过绘制出散点图可以看出:
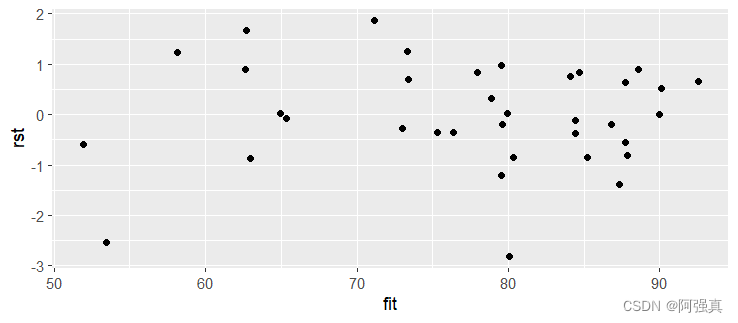
标准化残差值大致在区间(-2,3)内 ,存在可疑点。是否存在异方差性还需要进一步检测。
2.Goldfeld—Quandt检验
install.packages("lmtest")
library(lmtest)
as_flextable(gqtest(b))
 可以看出p值为0.4,即接受原假设,即不存在异方差
可以看出p值为0.4,即接受原假设,即不存在异方差
3.White检验和H.glesjser检验
White检验的统计量:
w = n ∗ R 2 C h i S q u a r e ( k ) w=n*R^2~ChiSquare\left( k \right) w=n∗R2 ChiSquare(k)
由于解释变量由5个,这个其实不太适合做white检验
可以参考这篇文章:
异方差与r语言实践
3.异方差的修正
加权最小二乘法:在r语言中代码非常简单
这里取权重为1/abs(e)
e<-resid(b)#e是标准化残差
b1<-lm(y~x1+x2+x3+x4+x5,weights=1/abs(e),data=a)
as_flextable(b1)
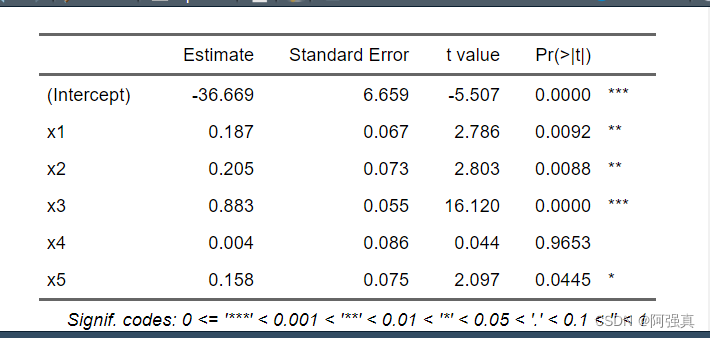
得到方程:
y e = − 36 e + 0.187 x 1 e + 0.205 x 2 e + 0.883 x 3 e + 0.004 x 4 e + 0.158 x 5 e \frac{y}{\sqrt{e}}=\frac{-36}{\sqrt{e}}+0.187\frac{x_1}{\sqrt{e}}+0.205\frac{x_2}{\sqrt{e}}+0.883\frac{x_3}{\sqrt{e}}+0.004\frac{x_4}{\sqrt{e}}+0.158\frac{x_5}{\sqrt{e}} ey=e−36+0.187ex1+0.205ex2+0.883ex3+0.004ex4+0.158ex5
其中e是残差
数据链接
链接:https://pan.baidu.com/s/1My6WTMXEZyIVfIM7A5oIbA?pwd=tjby
提取码:tjby
–来自百度网盘超级会员V4的分享