多元线性回归--R实现

1.多元线性回归

多元线性回归的代码实现如下：

> data3.1<-read.csv("C:/Users/Administrator/Desktop/data3.1.csv",head=TRUE)
> lm3.1<-lm(y~x1+x2+x3+x4+x5+x6+x7+x8+x9,data=data3.1)
> summary(lm3.1)

输出结果为：

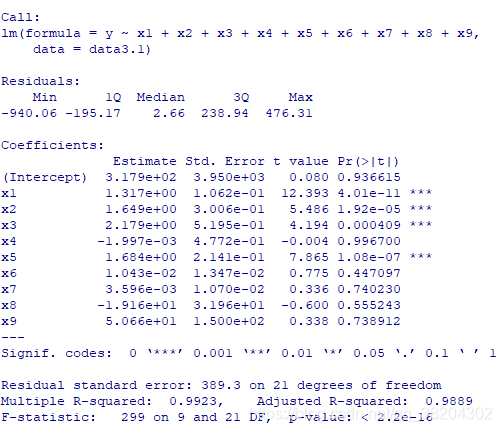
　　因而 $y$对9个自变量的线性回归方程为：
　　 $\hat{y}=320.6+1.317x_{1}+1.65x_{2}+2.179x_{3}-0.006x_{4}+1.684x_{5}$
　　　　　　　　　 $+0.01x_{6}+0.004x_{7}-19.13x_{8}+50.52x_{9}$
　　　　　　　
　　由summary()语句的输出结果可以看出，其中 $F$值为 $299$,对应的 $P$值为 $2.2e-16$，由此可知次回归方程整体上高度显著，即做出9个自变量整体对因变量 $y$产生显著线性影响的判断所犯错误的概率约为0.

2.方差分析

对于线性回归的方差分析，R语言中不仅可使用函数anova()得到方差分析表，还可以使用函数Anova()。

> library(car)
> Anova(lm3.1,type="III")

得到结果如下：

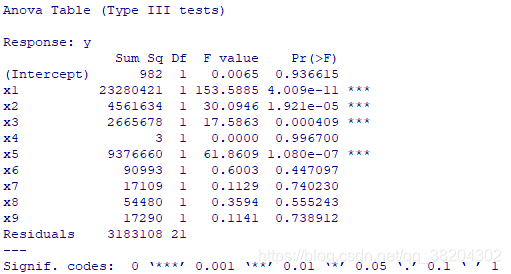
　　从上述结果中看出，在显著性水平 $\alpha =0.05$下，只有 $x_{1},x_{2},x_{3},x_{5}$对 $y$产生显著线性影响。

3.偏相关系数

偏相关系数测定在回归方程中已包含若干个自变量时，在引入某一个新的自变量时， $y$的剩余变差的相对减少量，它衡量某自变量对 $y$的变差减少的边际贡献。偏决定系数的算术平方根为片相关系数。

> data3.2<-read.csv("C:/Users/Administrator/Desktop/data3.2.csv",head=TRUE)
> lm3.2<-lm(y~x1+x2,data=data3.2)
>  r<-cor(data3.2)
> library(corpcor)
> pcor3.2<-cor2pcor(r)

输出结果为：
相关系数：

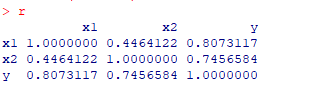
偏相关系数：

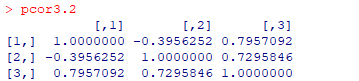
　　从上面结果可以看出， $r_{y1;2}=0.802$（ $r_{y1;2}$表示模型中已含有 $x_{2}$时再加入 $x_{1}$使 $y$的剩余变差的相对减少量）， $r_{y1;2}=0.739$，进一步计算可得到偏决定系数 $r_{y1;2}^{2}=0.643,r_{y2;1}^{2}=0.546$.
　　由相关系数矩阵可知， $y$与 $x_{1}$的简单相关系数 $r_{y1}=0.807$，则决定系数 $r_{y1}^{2}=(0.807)^{^{2}}=0.652$.
　　以上数据表明，用 $y$与 $x_{1}$做一元线性回归时， $x_{1}$能消除 $y$的变差SST的比例是62.5%，再引入 $x_{2}$时， $x_{2}$能消除剩余变差SSE的比例是54.6%，因而自变量 $x_{1}$和 $x_{2}$消除变差的总比例为 $1-(1-r_{y1}^{2})(1-r_{y2;1}^{2})=1(1-0.652)\times(1-0.546)=0.842$，这个值恰好是 $y$对 $x_{1}$和 $x_{2}$的二元香型回归的决定系数 $R^{2}$.