【高等数学】连续可导可微（定义+证明+记忆方法）

连续 可导 可微

1.定义

1.1 连续的定义

1. 定义1

   设y = f(x) 在点 $x_0$ 的某领域内有定义，若

   $\underset{\Delta x\to 0}{\lim }\Delta y=\underset{\Delta x\to 0}{\lim }[f(x_0+\Delta x)-f(x_0)]=0$

   则称 y = f(x)在点$x_0$处连续

2. 定义2

   设y = f(x) 在点 $x_0$ 的某领域内有定义，若

   $\underset{\Delta x\to 0}{\lim }f(x)=f(x_0)$

   则称y = f(x)在$x_0$处连续

1.2 可导的定义

设y = f(x) 在点 $x_0$ 的某领域内有定义，如果极限

$\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}=\underset{\Delta x\to 0}{\lim }\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$

存在，则称f(x)在点$x_0$处可导,记作$f^{\prime }(x_0)$也可以记作$y^{\prime }{|}_{x=x_0},\frac{dy}{dx}{|}_{x=x_0},\frac{df(x)}{dx}{|}_{x=x_0}$

1.3 可微的定义

设y = f(x) 在点 $x_0$ 的某领域内有定义，如果函数的增量$\Delta y=f(x_0+\Delta x)-f(x_0)$可以表示为

$\Delta y=A\Delta x+o(\Delta x),(\Delta x\to 0)$,

其中A为不依赖$\Delta x$的常数，则称函数在$x_0$处可微,而$A\Delta x$叫做函数$y=f(x)$在点$x_0$相对于自变量增量$\Delta x$的微分，记作dy，即
$dy=A\Delta x$

2.三者之间的关系

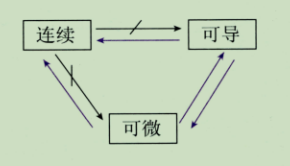
3.关系证明

3.1 可微和可导

1. 可微一定可导

   按上述定义，设函数在y=f(x)点可微，在函数两边除以$\Delta x$,得

   $\frac{\Delta y}{\Delta x}=A+\frac{o(\Delta x)}{\Delta x}$

   当$\Delta x\to 0$时，有

   $A=\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}=f^{\prime }(x_0)$

   符合可导的定义

2. 可导一定可微

   若$y=f(x_0)$在点$x_0$可导，则

   $\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}=f^{\prime }(x_0)$

   存在，根据极限与无穷小的关系(高等数学上第一章第四节定理1)，可写成

   $\frac{\Delta y}{\Delta x}=f^{\prime }(x_0)+\alpha$

   其中$\alpha \to 0(当\Delta x\to 0)$, 两边同乘$\Delta x$, 有

   $\Delta y=f^{\prime }(x_0)\Delta +\alpha \Delta x$

   因$\alpha \Delta x=o(\Delta x)$,且$f^{\prime }(x_0)$不依赖于$\Delta x$, 符合可微的定义

3.2 可导和连续

1. 可导(可微)一定连续

   Tips: 由上述证明可知，函数$f(x_0)$在$x_0$点可导的充分必要条件是函数$f(x_0)$在$x_0$点可微，故只要证明可导一定连续，就可推出可微一定连续。

   下面证可导一定连续

   设函数$y=f(x)$在x处可导，即

   $\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}=f^{\prime }(x)$,根据极限与无穷小的关系(高等数学上第一章第四节定理1)，可写成

   $\frac{\Delta y}{\Delta x}=f^{\prime }(x)+\alpha$

   其中$\alpha \to 0(当\Delta x\to 0)$, 两边同乘$\Delta x$, 有

   $\Delta y=f^{\prime }(x)\Delta x+\alpha \Delta x$

   由此可见，当$\Delta x\to 0$时，$\Delta y\to 0$,符合函数连续定义1，故可导一定连续

2. 连续不一定可导

   反例：$y=|x|$连续但不可导

   1. 证明1

      函数图像如下：

      

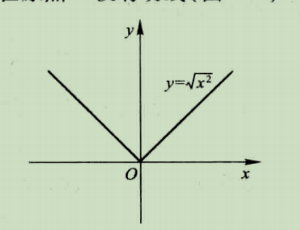
      导数的几何意义是切线的斜率，即$f^{\prime }(x_0)=tan\alpha$,易知原点左侧的斜率为-1，右侧为1，左右导数存在不相等，故不可导(可导的充分必要条件是左右极限存在且相等)

4.记忆方法

可导与可微是等价的，所以记住三者的关系，只要记住连续不一定可导\可微即可。

5.参考文章

1. 高等数学（第七版）
2. 武忠祥网课+高等数学基础篇

文章最后感谢华工悦哥的帮助指导