数学需要的不是天赋,而是少量的自由想象,但相信太过自由又会陷入疯狂。-----A.K.罗杰斯
一、张成的空间
1.在xy坐标系中,有两个非常特别的向量,一个指向正右方,长度为1,通常被称为“i帽”或者x方向的单位向量,另一个指向正上方,长度为1,通常被称为“j帽”或者y方向的单位向量。
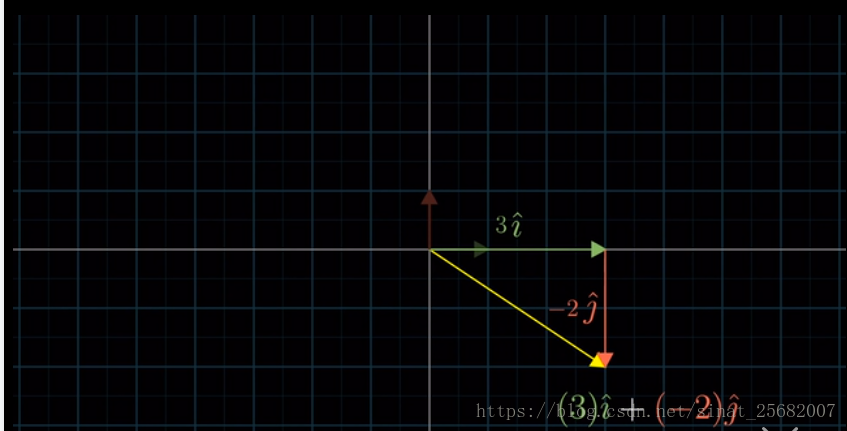
2.现在相信向量(3,-2)的x坐标是一个标量,它将i帽拉伸为原来的3倍,y坐标也是一个标量,它将j帽反向并拉伸为原来的2倍。从这个角度去看,这个向量实际上是两个经过缩放的向量的和。
3.“缩放向量并且相加”这一概念至关重要。被缩放的两个向量i帽和j帽也有特殊的名称。它们合起来被称为坐标系的基。这就是再说,当你把坐标看作标量时,基向量实际上就是这些标量所缩放的对象。
4.我们根据这两个特殊的基向量构建坐标系时,我们完全可以选择不同的基向量,获得一个完全合理的坐标系,所以每当我们用数字描述向量时,它都依赖于我们正在使用的基。
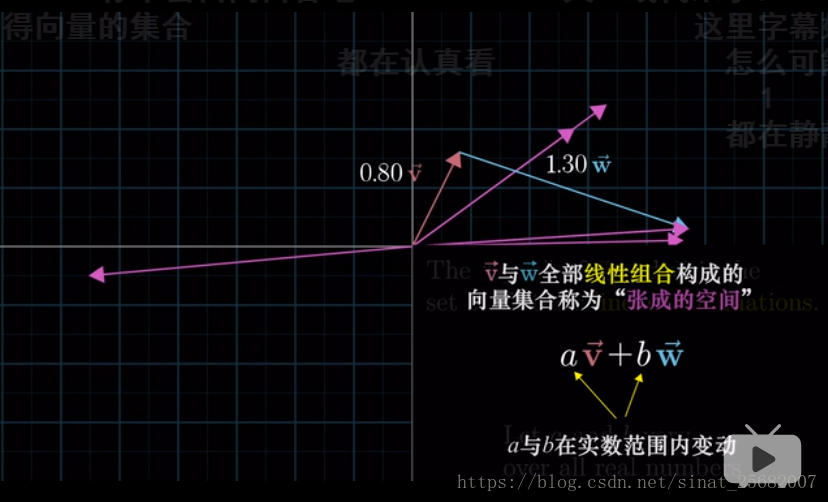
5.两个向量标量乘法之和的结果被称为这两个向量的线性组合。
6.为什么成为线性呢?如果固定其中一个标量,让另一个标量自由变化,所产生的向量的重点会描述出一条直线。
7.如果你让两个标量同时自由变化,考虑所有可能得到的向量,有两种可能,大部分情况下,对于一对初始向量,你能到达平面中的每一个点。但是也有糟糕的情况,当两个初始向量恰好共线时,所产生的向量的重点被限制在一条过原点的直线上。实际上还有第三种可能,两个向量都是零向量,那就乖乖呆在原点。
8.所有可以表示为定向量线性组合的向量集合,被称为给定向量张成的空间。
9.对于大部分二维向量来说,它们张成的空间是所有二维向量的集合,但当共线时,它们张成的空间就是终点落在一条直线上的向量的额集合。
二、向量与点
1.想象将所有二维向量填满平面时,你会觉得非常拥挤,为了对付这种情况,通常我们就用向量的重点代表该向量,而像以往一样,它的起点仍旧位于原点。
2.单个向量看作箭头,多个向量看作点。
三、在三维空间中看张成空间
1.举个例子,在三维空间中取两个指向不同方向的向量,他们张成的空间是什么呢?这两个向量张成的空间就是他们所有可能的线性组合,也就是缩放再相加之后所有可能得到的向量。