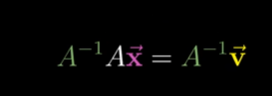思维导图

行列式的几何意义
- 在二维空间中矩阵对应的行列式:表示该矩阵所描述的线性变换对某一块区域的面积的缩放程度
- 在三维空间中自然就表示三维立体体积的缩放程度,n维空间依次类推。
注:因为原体积是棱边为1的立方体(以各个基向量组成的平面/空间图形,在研究缩放时具有代表性,后续会解释这一点),而立方体体积为1,所以行列式的数值也可以看成是变换后得到的平行六面体的体积。
- 详细剖析行列式中各个值的大小
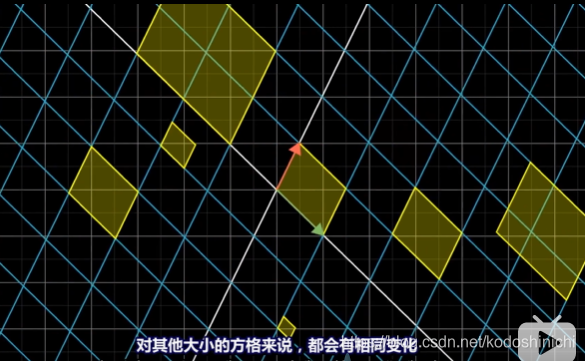
平面上任意一块区域的面积都有着相同的缩放系数
- 可以用x轴和y轴的基向量围成的四边形作为代表图形,来研究空间变换前后的面积缩放系数。
- 原因:
①在进行线性变换的时候,“网格线保持平行且等距分布”,故所有方格会有相同的大小变换
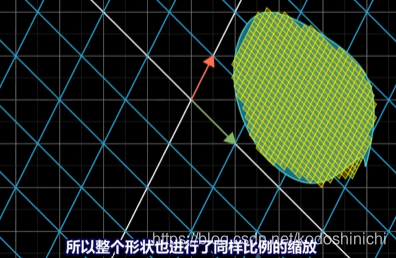
②非方格的图形也可以有方格进行良好近似
行列式的符号与空间/平面定向
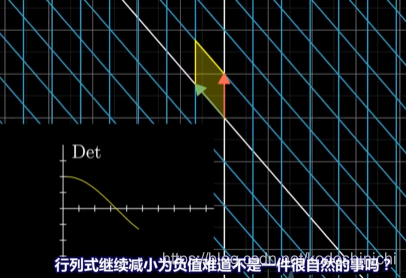
- 行列式为0:
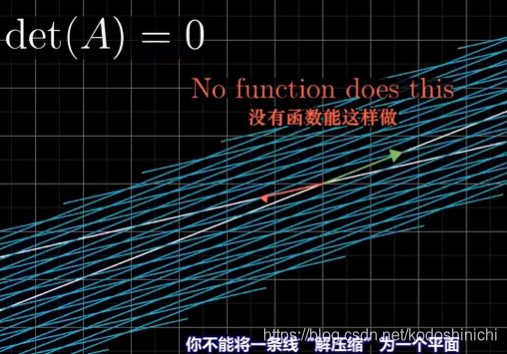
①二维行列式说明将一个平面图形压缩成了一条直线或一个点。
②三维行列式说明将一个立体图形压缩成了一个平面或一条直线。
③一个矩阵的行列式是否为0↔
这个矩阵代表的变换是否将空间压缩到更小的维度上
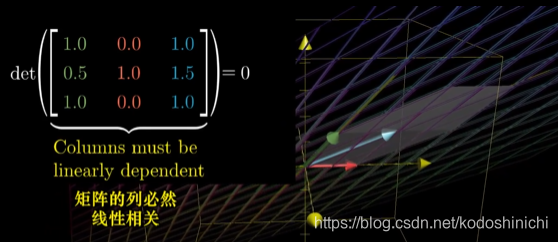
④行列式为0↔行列式对应的矩阵的列必然线性相关
理解:上一节中讲过了矩阵中某一列向量对于张开的空间的维度没有贡献的时候,这个矩阵的列是线性相关的,而一个三维变换矩阵将一个立方体变换成平面或直线或一个点,说明其张成的空间发生了降维,则必然出现了对张成空间无用的向量。
2.平面的定向:可以从微积分中的二维三维积分中定义的方向,以及平面的法向量都是有方向的这一点来理解。
①平面的反转——改变平面的定向
②i与j基向量之间的相对位置发生了改变——改变了平面的定向
③行列式的变换趋势:
3.空间的定向——左手定则和右手定则
如果右手定则在变换之后无法满足,只能使用以下左手定则,则说明定向发生了变化。
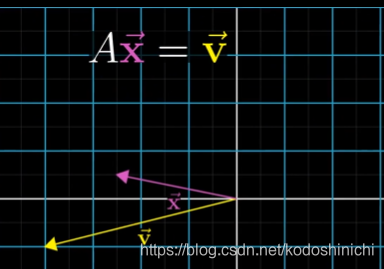
线性方程组与其矩阵形式
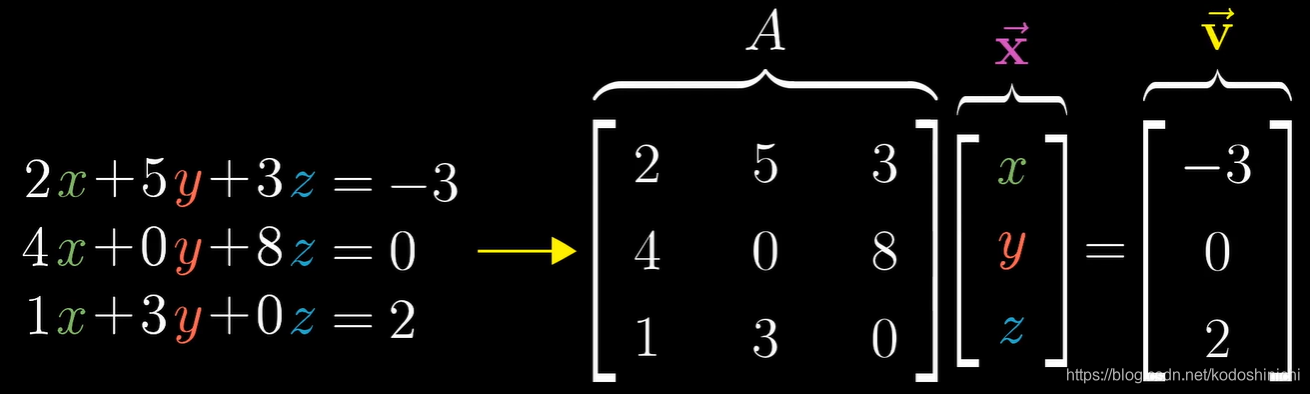
理解:求解线性方程组Ax=v,也就是想要找到一个向量x通过线性变换A的作用变成向量v。
行列式在线性方程组求解过程中的理解
①当矩阵A的行列式不为0的时候,说明原向量空间并没有被压缩成一个更低维的空间,这个时候有且仅有一个向量能够从x变换成v,想要求解x,对v做相应的逆变换即可。
而本质上跟踪逆变换就是求解原线性变换对应矩阵的逆矩阵,逆矩阵也是可以看做一个线性变换的。
②当行列式的值为0时,不存在逆矩阵,因为没有哪一种线性变换可以把一个低维空间里的向量变换成一个更高维空间的向量。
理解:“这样的线性变换不存在”的原因还可以是,一个线性变换本质上就是一个函数,函数是不能有一对多的输出的,但是从一个低维空间向高维空间回望的时候,往往是一对多的情况,这个时候也就不能称之为函数。
逆矩阵
- 定义:逆矩阵是满足以下条件的唯一矩阵:
对空间进行逆矩阵对应的变换后再进行原矩阵的变换,空间会回到初始状态。
- 理解与延伸定义
①两个线性变换相继作用可以解释成该两个线性变换对应的矩阵进行乘法运算。
②引入矩阵逆的数学定义,AA-1 =E
其中“什么都不做的矩阵”称作为恒等变换矩阵,矩阵中的两列对应的基向量并未发生任何变化。- 逆矩阵的求解
两边同乘上矩阵A的逆矩阵相当于对向量空间进行逆向线性变换并跟踪其状态。
行列式为0时线性方程组的求解
- 行列式为0,不存在逆矩阵,也是可能存在解的
因为整个空间经过该线性变换后被压缩成一个更低维的空间,比如下图中,原空间最终被压缩成一条直线,若最后你跟踪的v向量就在该直线上,那么当然是存在解x的,原空间中的任意一个向量经过该变换都会落在该直线上。
- 将此处我们建立的直观印象和“利用矩阵判定方程组的解”的计算思维相对照:
对于矩阵方程AX=b,当r(A,b)=r(A)的时候,若A为可逆矩阵则有唯一解,若A为不可逆矩阵则有无穷解;当r(A,b)≠r(A)的时候,方程组就是无解的。
因此对于一个行列式为0的系数矩阵,要么就对应无解,要么就有无穷解。
- 矩阵的秩
①原空间在线性变换的作用下被压缩成低维空间的程度不同,方程组有解的情况就不同。
②矩阵的秩:变换之后向量空间的维度
列空间与秩
一个矩阵(不论行列式是否为0)其变换后所有可能的向量构成的集合就称为列空间
所谓变换后的所有向量,这些向量都是由变换后的矩阵中的基向量所决定的,因此也可以说列空间是该矩阵的基(列)向量所张成的空间。
- 定义了列空间的概念之后,也可以说一个矩阵的秩就是该矩阵的列空间的维数
- 因为变换前后零向量不变,(线性变换保持原点不变形),因此任何一个列空间中均含有零向量。且对于一个变换而言,具有压缩性质的变换,往往会把一整个直线或一整个平面(更高维以此类推)中的向量全部转换成零向量。
- 当矩阵的秩达到最大,即秩等于矩阵的列的维数,此时就称这个矩阵为满秩矩阵
零空间
1.定义: 变换后落在原点的向量的集合,就称为矩阵的零空间或“核”
2.对于一个齐次矩阵方程Ax = 0来说,其零空间也就是对应的该方程的解空间,因为零空间给出了所有经变换后为零向量的原向量,而这恰恰就是解矩阵方程所要求的东西。
概述
1.每一个线性方程组都有一个线性变换与之对应
2.当该矩阵A存在逆矩阵的时候,就可以使用对应的逆矩阵进行方程求解
3.矩阵的列空间指示我们什么时候这个方程对应有解
4. 零空间指示方程可能求解出来的情况
5.如果仔细阅读了上面的一些例子之后,会发现作者的讨论都是基于方阵而言,换句话说,将线性方程组抽象成变换再抽象成矩阵方程的过程中,是加了一个限制条件的——变量的个数和方程的个数相等。
非方阵的解读
1.一个矩阵的行列数目相同(这个矩阵是个方阵)除了从以上第5点的两个角度来理解,还可以从空间变换的角度来理解:一个nxn的方阵,说明该矩阵对应的变换就是把一个n维的空间变换成另一个n维的空间(或其子空间,这取决于矩阵本身的性质)。
2.核心观点:即使一个矩阵不是方阵,用变换的角度去理解的时候,依然是从“变换后的基向量”的角度去理解矩阵的含义。
3.示例:对一个3x2矩阵的理解
①输入与输出空间的直观印象
②变换矩阵的直观理解——变换后的基向量的坐标表示
③矩阵的行数表示变换后的空间维数;矩阵列数则表示变换前的空间维数
④一个3x2矩阵的列空间对应的就是三维空间中一个过原点的二维平面,且该矩阵依然是满秩的——
a.(计算思维理解)r=2=列的个数
b.(直观印象理解)输入空间的维度等于列空间的维度
5.线性变换的另外一种理解
①回顾:之前对线性变换的定义是保持网格线的平行,且原点依然映射成原点的一种变换
②寻求另一种解释的原因:因为在进行不同维度空间的映射过程中,考虑用网格线去理解变化会显得十分杂乱。
③另一种解释:如果在一条直线上有一系列等距离分布的点,在映射到另一空间之后他们依然会保持等距分布。
原视频
【官方双语/合集】线性代数的本质 - 系列合集-07
【官方双语/合集】线性代数的本质 - 系列合集-08