文章目录
CSDN提示我字数太多,一篇发不下,只好拆分开
关于
- 标准DH模型
- 改进DH模型
- 机器人正运动学
的相关内容详见第一篇文章:
❤ 2023.6.19 ❤
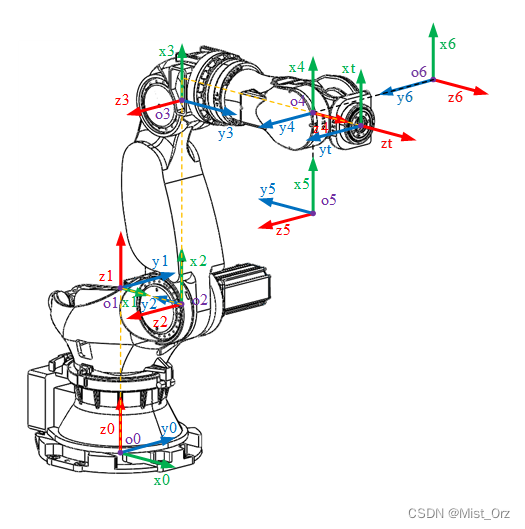
机器人逆运动学
※ 代数解、几何解,解析解(封闭解)、数值解的含义与联系
说起来我刚碰到这几个概念的时候还是挺晕的,和别人交流之后发现晕的不止我一个,经常有人把概念搞混、搞错。
下面有请ChatGPT先来回答一下
然后我总结一下
代数解和几何解都属于解析解(封闭解),他们的特点是可以列出具体的方程,求得的结果是精确的。不一样的地方是,代数解是根据矩阵的特性,通过特定元素相等的方法建立方程组,求解出未知数;而几何解是通过机器人的几何关系建立方程组,求解未知数。
只有特定构型的机器人存在解析解,不过好在我们平时用到的机器人大多数都是特定构型的。
数值解与解析解相对应,特点是运算过程靠迭代,求得的结果是近似解。他适用于所有机器人,包括特殊构型和一般构型,大多在不存在解析解的机器人上使用。
针对ZK-500机器人,因为属于后三轴交于一点的特殊构型,所以这里使用解析法求机器人逆解。
首先将位姿描述矩阵写成如下形式
6 0 T = [ n x o x a x p x n y o y a y p y n z o z a z p z 0 0 0 1 ] = 1 0 T ( θ 1 ) 2 1 T ( θ 2 ) 3 2 T ( θ 3 ) 4 3 T ( θ 4 ) 5 4 T ( θ 5 ) 6 5 T ( θ 6 ) {_6^0}T=\left[\begin{matrix}n_x&o_x&a_x&p_x\\n_y&o_y&a_y&p_y\\n_z&o_z&a_z&p_z\\0&0&0&1\\\end{matrix}\right]={_1^0}T\left(\theta_1\right)\ _2^1T\left(\theta_2\right)\ _3^2T\left(\theta_3\right)\ _4^3T\left(\theta_4\right)\ _5^4T\left(\theta_5\right)\ _6^5T\left(\theta_6\right) 60T= nxnynz0oxoyoz0axayaz0pxpypz1 =10T(θ1) 21T(θ2) 32T(θ3) 43T(θ4) 54T(θ5) 65T(θ6)
△ 代数解求 θ 1 \theta_1 θ1、 θ 2 \theta_2 θ2、 θ 3 \theta_3 θ3
※参考资料
→→→【MD-H模型运动学正解、逆解及姿态角的解算验证】
这真是个宝藏作者了
→→→《机器人学导论》(John J Craig)
※ 关于为何使用atan2()函数求解
A t a n 2 ( ) \mathrm{Atan2}\left(\right) Atan2(),这个函数与 A t a n ( ) \mathrm{Atan}\left(\right) Atan()一样是求反正切,但是他的值域为 ( − π , π ) (-\pi,\pi) (−π,π),可以得到角度对应的象限,是增强版的 A t a n ( ) \mathrm{Atan}\left(\right) Atan()。
具体可以参考
→→→atan2()
→→→atan2 vs atan
至于为什么要用这个函数,这一点开始我也非常疑惑,有的转角在求出sin值或者cos值后,理论上就可以用反正弦/反余弦函数求解出对应的角度了,为什么还要多此一举同时求出sin与cos,然后相除再用atan2()来求解呢?
经过查找资料,我看到了这篇文章
我总结一下,大概意思就是直接用反正弦/反余弦函数也不是不行,但是他们的值域范围比较小,机器人的关节活动范围可达 ( − π , π ) (-\pi,\pi) (−π,π),使用反正弦/反余弦函数求解的话需要充分考虑不同位姿的取值范围然后进行判断。而atan2()函数的取值范围为 ( − π , π ) (-\pi,\pi) (−π,π),很多情况下省去了额外的判断过程。
并且arcsin()/arccos()函数在一些特殊点时缺乏定义,会导致计算结果的误差放大,而atan2()函数不存在这个问题。
atan2()函数定义

- 使用atan2()函数需要注意的问题
但是根据文章【为什么机器人运动学逆解最好采用双变量反正切函数atan2而不用反正/余弦函数?】所说,使用atan2()之后并不是万无一失了,同样需要注意一些问题:
1、x=0,y=0时的定义
2、x或y在经过0点时函数的值的跳变
具体解决方法参见上面这篇文章
○ 求解 θ 1 \theta_1 θ1
首先将上式中包含 θ 1 \theta_1 θ1的部分移动到方程的左边
[ 1 0 T ( θ 1 ) ] − 1 6 0 T = 2 1 T ( θ 2 ) 3 2 T ( θ 3 ) 4 3 T ( θ 4 ) 5 4 T ( θ 5 ) 6 5 T ( θ 6 ) {\left[{_1^0}T\left(\theta_1\right)\right]^{-1}}\ _6^0T={_2^1}T\left(\theta_2\right)\ _3^2T\left(\theta_3\right)\ _4^3T\left(\theta_4\right)\ _5^4T\left(\theta_5\right)\ _6^5T\left(\theta_6\right) [10T(θ1)]−1 60T=21T(θ2) 32T(θ3) 43T(θ4) 54T(θ5) 65T(θ6)
将 1 0 T {_1^0}T 10T求逆,等式写成如下形式
[ c 1 s 1 0 0 − s 1 c 1 0 0 0 0 1 − d 1 0 0 0 1 ] [ n x o x a x p x n y o y a y p y n z o z a z p z 0 0 0 1 ] = 6 1 T \left[\begin{matrix}c_1&s_1&0&0\\-s_1&c_1&0&0\\0&0&1&-d_1\\0&0&0&1\\\end{matrix}\right]\left[\begin{matrix}n_x&o_x&a_x&p_x\\n_y&o_y&a_y&p_y\\n_z&o_z&a_z&p_z\\0&0&0&1\\\end{matrix}\right]={_6^1}T c1−s100s1c100001000−d11 nxnynz0oxoyoz0axayaz0pxpypz1 =61T
求解出 6 1 T {_6^1}T 61T后,通过观察等式两边的矩阵,令元素(2,4)相等得到
− s 1 p x + c 1 p y = 0 -s_1p_x+c_1p_y=0 −s1px+c1py=0
- ※ 【这个方程是怎么得到的】
这个求解过程内容比较多,我姑且用matlab算了一下。。。
- 等式左边矩阵(每个方括号代表一行)
[nx*cos(Q1) + ny*sin(Q1),
ox*cos(Q1) + oy*sin(Q1),
ax*cos(Q1) + ay*sin(Q1),
px*cos(Q1) + py*sin(Q1)]
[ny*cos(Q1) - nx*sin(Q1),
oy*cos(Q1) - ox*sin(Q1),
ay*cos(Q1) - ax*sin(Q1),
py*cos(Q1) - px*sin(Q1)]
[nz,oz,az,pz - d1]
[0,0,0,1]
- 等式右边矩阵(每个方括号代表一行)
[- cos(Q6)*(sin(Q2 + Q3)*sin(Q5) - cos(Q2 + Q3)*cos(Q4)*cos(Q5)) - cos(Q2 + Q3)*sin(Q4)*sin(Q6),
sin(Q6)*(sin(Q2 + Q3)*sin(Q5) - cos(Q2 + Q3)*cos(Q4)*cos(Q5)) - cos(Q2 + Q3)*cos(Q6)*sin(Q4),
sin(Q2 + Q3)*cos(Q5) + cos(Q2 + Q3)*cos(Q4)*sin(Q5),
a1 + a3*cos(Q2 + Q3) + d4*sin(Q2 + Q3) + a2*cos(Q2)]
[- cos(Q4)*sin(Q6) - cos(Q5)*cos(Q6)*sin(Q4),
cos(Q5)*sin(Q4)*sin(Q6) - cos(Q4)*cos(Q6),
sin(Q4)*sin(Q5),
0]
[cos(Q6)*(cos(Q2 + Q3)*sin(Q5) + sin(Q2 + Q3)*cos(Q4)*cos(Q5)) - sin(Q2 + Q3)*sin(Q4)*sin(Q6),
- sin(Q6)*(cos(Q2 + Q3)*sin(Q5) + sin(Q2 + Q3)*cos(Q4)*cos(Q5)) - sin(Q2 + Q3)*cos(Q6)*sin(Q4),
sin(Q2 + Q3)*cos(Q4)*sin(Q5) - cos(Q2 + Q3)*cos(Q5),
a3*sin(Q2 + Q3) - d4*cos(Q2 + Q3) + a2*sin(Q2)]
[0,0,0,1]
果然包含 θ 1 \theta_1 θ1(这里是 Q 1 Q_1 Q1)的元素里面就(2,4)最好算。。。
式中, p x p_x px、 p y p_y py均为已知,则 θ 1 \theta_1 θ1可表示为:
θ 1 = A t a n 2 ( p y , p x ) \theta_1=\mathrm{Atan2}\left(p_y,p_x\right) θ1=Atan2(py,px)
需要注意的是输入变量先 p y p_y py再 p x p_x px。
因为 tan θ = p y p x \tan{\theta}=\frac{p_y}{p_x} tanθ=pxpy,也就是先输入分子,再输入分母。
此处存在两组解:
θ 1 = A t a n 2 ( p y , p x ) \theta_1=\mathrm{Atan2}\left(p_y,p_x\right) θ1=Atan2(py,px)
或 θ 1 ′ = A t a n 2 ( − p y , − p x ) \theta_1^\prime=\mathrm{Atan2}\left(-p_y,-p_x\right) θ1′=Atan2(−py,−px)
- matlab代码实现
%% theta1求解
%theta1可能的解有两组
theta1_1=atan2(py,px);
theta1_2=atan2(-py,-px);
○ 求解 θ 3 \theta_3 θ3
令上面等式中矩阵元素(1,4)和(3,4)左右相等得:
c 1 p x + s 1 p y = a 1 + a 2 c 2 + a 3 c 23 + d 4 s 23 p z − d 1 = a 2 s 2 + a 3 s 23 − d 4 c 23 c_1p_x+s_1p_y=a_1+a_2c_2+a_3c_{23}+d_4s_{23}\\ p_z-d_1=a_2s_2+a_3s_{23}-d_4c_{23} c1px+s1py=a1+a2c2+a3c23+d4s23pz−d1=a2s2+a3s23−d4c23
等号左右平方和得
m 2 + n 2 = a 2 2 + a 3 2 + d 4 2 + 2 a 2 ( a 3 c 3 + d 4 s 3 ) m^2+n^2=a_2^2+a_3^2+d_4^2+2a_2\left(a_3c_3+d_4s_3\right) m2+n2=a22+a32+d42+2a2(a3c3+d4s3)
其中:
m = c 1 p x + s 1 p y − a 1 n = p z − d 1 m=c_1p_x+s_1p_y-a_1\\ n=p_z-d_1 m=c1px+s1py−a1n=pz−d1
关于这一步的计算过程:
我用这段代码演示:
syms a1 a2 a3 d4 theta2 theta3
m=a2*cos(theta2)+a3*cos(theta2+theta3)+d4*sin(theta2+theta3);
n=a2*sin(theta2)+a3*sin(theta2+theta3)-d4*cos(theta2+theta3);
k=m^2 + n^2
% 展开表达式为多项式形式
K1 = expand(m^2 + n^2)
%K = collect(K, [a1 a2 a3 d4]);
% 化简多项式
K2=simplify(K1)
% 整理多项式的项
k3=collect(K2)
结果:
k =
(a3*cos(theta2 + theta3) + d4*sin(theta2 + theta3) + a2*cos(theta2))^2 + (a3*sin(theta2 + theta3) - d4*cos(theta2 + theta3) + a2*sin(theta2))^2
K1 =
a2^2*cos(theta2)^2 + a2^2*sin(theta2)^2 + a3^2*cos(theta2)^2*cos(theta3)^2 + d4^2*cos(theta2)^2*cos(theta3)^2 + a3^2*cos(theta2)^2*sin(theta3)^2 + a3^2*cos(theta3)^2*sin(theta2)^2 + d4^2*cos(theta2)^2*sin(theta3)^2 + d4^2*cos(theta3)^2*sin(theta2)^2 + a3^2*sin(theta2)^2*sin(theta3)^2 + d4^2*sin(theta2)^2*sin(theta3)^2 + 2*a2*a3*cos(theta2)^2*cos(theta3) + 2*a2*a3*cos(theta3)*sin(theta2)^2 + 2*a2*d4*cos(theta2)^2*sin(theta3) + 2*a2*d4*sin(theta2)^2*sin(theta3)
K2 =
a2^2 + 2*cos(theta3)*a2*a3 + 2*sin(theta3)*a2*d4 + a3^2 + d4^2
k3 =
a2^2 + 2*cos(theta3)*a2*a3 + 2*sin(theta3)*a2*d4 + a3^2 + d4^2
令 H = ( m 2 + n 2 − a 2 2 − a 3 2 − d 4 2 ) / 2 a 2 H=\left(m^2+n^2-a_2^2-a_3^2-d_4^2\right)/2a_2 H=(m2+n2−a22−a32−d42)/2a2
则可将等式表示为:
a 3 c 3 + d 4 s 3 = H a_3c_3+d_4s_3=H a3c3+d4s3=H
可得:
θ 3 = A t a n 2 ( H , ± a 3 2 + d 4 2 − H 2 ) − A t a n 2 ( a 3 , d 4 ) \theta_3=\mathrm{Atan2}\left(H,\pm\sqrt{a_3^2+d_4^2-H^2}\right)-\mathrm{Atan2}\left(a_3,d_4\right) θ3=Atan2(H,±a32+d42−H2)−Atan2(a3,d4)
由于正负号的存在, θ 3 \theta_3 θ3存在两组解。
- ※ 【关于这一步是怎么来的】
我没有找到转换成反正切的具体的内容,但是这个推导过程可以参考
- matlab代码实现
%% theta3求解
%theta1的取值已经确定,但是因为theta1有两组可能得解,所以这里实际上m有两组取值,这里只给出一组
m=cos(theta1)*px+sin(theta1)*py-a1;
n=pz-d1;
H=(m^2+n^2-a2^2-a3^2-d4^2)/(2*a2);
theta3_1=atan2(H,sqrt(a3^2+d4^2-H^2))-atan2(a3,d4);
theta3_2=atan2(H,-sqrt(a3^2+d4^2-H^2))-atan2(a3,d4);
○ 求解 θ 2 \theta_2 θ2
关于\theta_2$的求解,我尝试了若干种方法。
· 机器人学导论的方法(失败的尝试)
首先,我按照《机器人学导论》(John J Craig)这本教材中记录的方法进行尝试。
众所周知,《机器人学导论》中都是以PUMA560为案例的,而PUMA560的结构与现在常用的工业机器人的构型并不相同(主要是和我研究的机器人不同),所以并不能直接拿来用。这里是参照其步骤进行计算的。
第一步,整理机器人末端位姿描述矩阵的计算式如下
[ 3 0 T ( θ 2 ) ] − 1 6 0 T = 4 3 T ( θ 4 ) 5 4 T ( θ 5 ) 6 5 T ( θ 6 ) [{_3^0}T\left(\theta_2\right)]^{-1}\ {_6^0}T={_4^3}T\left(\theta_4\right)\ {_5^4}T\left(\theta_5\right)\ {_6^5}T\left(\theta_6\right)\ [30T(θ2)]−1 60T=43T(θ4) 54T(θ5) 65T(θ6)
令等号两边矩阵元素(1,4)和(2,4)相等,得到如下等式
( p z − d 1 ) sin ( θ 23 ) − a 1 cos ( θ 23 ) − a 2 cos ( θ 3 ) + . . . p x cos ( θ 1 ) cos ( θ 23 ) + p y sin ( θ 1 ) cos ( θ 23 ) = a 3 ( p z − d 1 ) cos ( θ 23 ) + a 1 sin ( θ 23 ) + a 2 sin ( θ 3 ) − . . . p y cos ( θ 1 ) cos ( θ 23 ) + p x sin ( θ 1 ) cos ( θ 23 ) = − d 4 (p_z-d_1)\sin(\theta_{23})-a_1\cos(\theta_{23})-a_2\cos(\theta_3)+...\\p_x\cos(\theta_1)\cos(\theta_{23})+p_y\sin(\theta_1)\cos(\theta_{23})=a_3\\ (p_z-d_1)\cos(\theta_{23})+a_1\sin(\theta_{23})+a_2\sin(\theta_3)-...\\p_y\cos(\theta_1)\cos(\theta_{23})+p_x\sin(\theta_1)\cos(\theta_{23})=-d_4 (pz−d1)sin(θ23)−a1cos(θ23)−a2cos(θ3)+...pxcos(θ1)cos(θ23)+pysin(θ1)cos(θ23)=a3(pz−d1)cos(θ23)+a1sin(θ23)+a2sin(θ3)−...pycos(θ1)cos(θ23)+pxsin(θ1)cos(θ23)=−d4
- 计算过程如下
syms Q1 Q2 Q3 Q4 Q5 Q6 d1 d4 dt a1 a2 a3 nx ny nz ox oy oz ax ay az px py pz
%ZK-500连杆间齐次变换矩阵
T_01 =[ cos(Q1), -sin(Q1), 0, 0
sin(Q1), cos(Q1), 0, 0
0, 0, 1, d1
0, 0, 0, 1];
T_12 =[ cos(Q2), -sin(Q2), 0, a1
0, 0, -1, 0
sin(Q2), cos(Q2), 0, 0
0, 0, 0, 1];
T_23 =[ cos(Q3), -sin(Q3), 0, a2
sin(Q3), cos(Q3), 0, 0
0, 0, 1, 0
0, 0, 0, 1];
T_34 =[ cos(Q4), -sin(Q4), 0, a3
0, 0, -1, -d4
sin(Q4), cos(Q4), 0, 0
0, 0, 0, 1];
T_45 =[ cos(Q5), -sin(Q5), 0, 0
0, 0, 1, 0
-sin(Q5), -cos(Q5), 0, 0
0, 0, 0, 1];
T_56 =[ cos(Q6), -sin(Q6), 0, 0
0, 0, -1, 0
sin(Q6), cos(Q6), 0, 0
0, 0, 0, 1];
T_6t=[ 1 0 0 0
0 1 0 0
0 0 1 dt
0 0 0 1];
% 计算T_06和T_16的逆矩阵
T_06=[nx ox ax px;ny oy ay py;nz oz az pz;0 0 0 1];
T_03=T_01*T_12*T_23;
T_36=T_34*T_45*T_56;
% 计算T_01的逆矩阵
T_03_inv = inv(T_03);
%输出结果并化简
T_left=T_03_inv*T_06;
disp("等式左边矩阵:")
%T_left=simplify(T_left)
T_left
disp("等式右边矩阵:")
simplify(T_36)
结果如下
T_left =
[nz*cos(Q2)*sin(Q3) + nz*cos(Q3)*sin(Q2) - nx*cos(Q1)*sin(Q2)*sin(Q3) - ny*sin(Q1)*sin(Q2)*sin(Q3) + nx*cos(Q1)*cos(Q2)*cos(Q3) + ny*cos(Q2)*cos(Q3)*sin(Q1),
oz*cos(Q2)*sin(Q3) + oz*cos(Q3)*sin(Q2) - ox*cos(Q1)*sin(Q2)*sin(Q3) - oy*sin(Q1)*sin(Q2)*sin(Q3) + ox*cos(Q1)*cos(Q2)*cos(Q3) + oy*cos(Q2)*cos(Q3)*sin(Q1),
az*cos(Q2)*sin(Q3) + az*cos(Q3)*sin(Q2) - ay*sin(Q1)*sin(Q2)*sin(Q3) + ax*cos(Q1)*cos(Q2)*cos(Q3) + ay*cos(Q2)*cos(Q3)*sin(Q1) - ax*cos(Q1)*sin(Q2)*sin(Q3),
pz*sin(Q2 + Q3) - d1*sin(Q2 + Q3) - a1*cos(Q2 + Q3) - a2*cos(Q3) + (px*cos(Q1 + Q2 + Q3))/2 + (py*sin(Q1 + Q2 + Q3))/2 + (px*cos(Q2 - Q1 + Q3))/2 - (py*sin(Q2 - Q1 + Q3))/2]
[nz*cos(Q2)*cos(Q3) - nz*sin(Q2)*sin(Q3) - ny*cos(Q2)*sin(Q1)*sin(Q3) - ny*cos(Q3)*sin(Q1)*sin(Q2) - nx*cos(Q1)*cos(Q2)*sin(Q3) - nx*cos(Q1)*cos(Q3)*sin(Q2),
oz*cos(Q2)*cos(Q3) - oz*sin(Q2)*sin(Q3) - oy*cos(Q2)*sin(Q1)*sin(Q3) - oy*cos(Q3)*sin(Q1)*sin(Q2) - ox*cos(Q1)*cos(Q2)*sin(Q3) - ox*cos(Q1)*cos(Q3)*sin(Q2),
az*cos(Q2)*cos(Q3) - az*sin(Q2)*sin(Q3) - ax*cos(Q1)*cos(Q2)*sin(Q3) - ax*cos(Q1)*cos(Q3)*sin(Q2) - ay*cos(Q2)*sin(Q1)*sin(Q3) - ay*cos(Q3)*sin(Q1)*sin(Q2),
pz*cos(Q2 + Q3) - d1*cos(Q2 + Q3) + a1*sin(Q2 + Q3) + a2*sin(Q3) + (py*cos(Q1 + Q2 + Q3))/2 - (px*sin(Q1 + Q2 + Q3))/2 - (py*cos(Q2 - Q1 + Q3))/2 - (px*sin(Q2 - Q1 + Q3))/2]
[
nx*sin(Q1) - ny*cos(Q1),
ox*sin(Q1) - oy*cos(Q1),
ax*sin(Q1) - ay*cos(Q1),
px*sin(Q1) - py*cos(Q1)
]
[0,0,0, 1]
等式右边矩阵:
[
cos(Q4)*cos(Q5)*cos(Q6) - sin(Q4)*sin(Q6),
- cos(Q6)*sin(Q4) - cos(Q4)*cos(Q5)*sin(Q6),
cos(Q4)*sin(Q5),
a3
]
[
cos(Q6)*sin(Q5),
-sin(Q5)*sin(Q6),
-cos(Q5),
-d4]
[cos(Q4)*sin(Q6) + cos(Q5)*cos(Q6)*sin(Q4),
cos(Q4)*cos(Q6) - cos(Q5)*sin(Q4)*sin(Q6),
sin(Q4)*sin(Q5),
0]
[0, 0, 0, 1]
然后让ChatGPT帮我化简
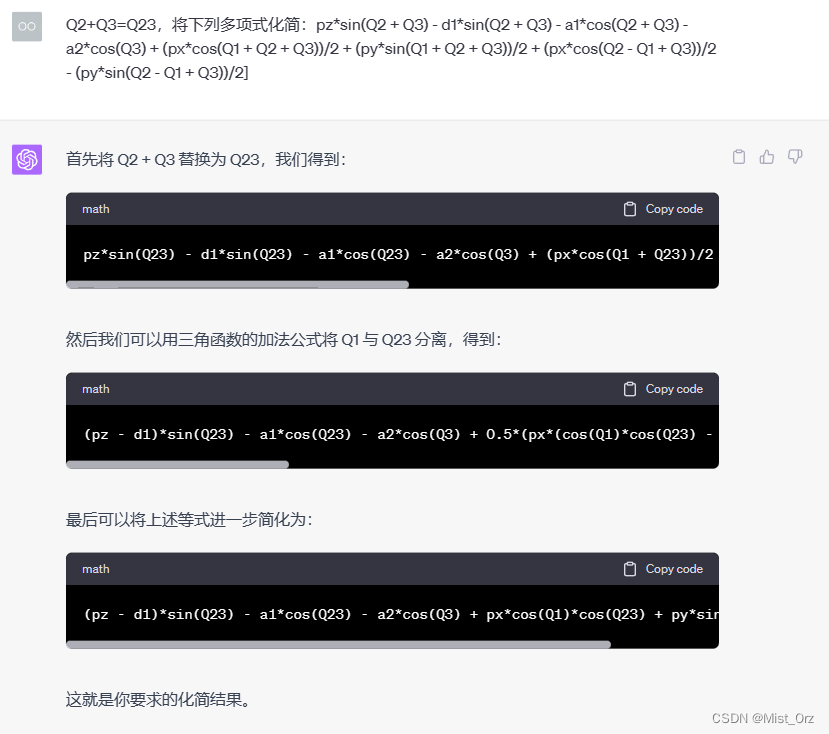
最后结果就是这个
(pz - d1)*sin(Q23) - a1*cos(Q23) - a2*cos(Q3) + px*cos(Q1)*cos(Q23) + py*sin(Q1)*cos(Q23)=a3;
(pz - d1)*cos(Q23) + a1*sin(Q23) + a2*sin(Q3) - py*cos(Q1)*cos(Q23) + px*sin(Q1)*cos(Q23)=-d4;
此时等式中未知的只有 s 23 s_{23} s23和 c 23 c_{23} c23,将其设为未知数,(理论上)就可以解出来 θ 2 + θ 3 \theta_2+\theta_3 θ2+θ3
设
m 1 = c 1 p x + s 1 p y − a 1 m 2 = p z − d 1 m 3 = a 3 + a 2 c 3 m_1=c_1p_x+s_1p_y-a_1\\ m_2=p_z-d_1\\ m_3=a_3+a_2c_3 m1=c1px+s1py−a1m2=pz−d1m3=a3+a2c3
n 1 = − c 1 p y − s 1 p x − d 1 n 2 = a 1 n 3 = − d 4 − a 2 s 3 n_1=-c_1p_y-s_1p_x-d_1\\ n_2=a_1\\ n_3=-d_4-a_2s_3 n1=−c1py−s1px−d1n2=a1n3=−d4−a2s3
将方程组整理为
m 1 c 23 + m 2 s 23 = m 3 n 1 c 23 + n 2 s 23 = n 3 m_1c_{23}+m_2s_{23}=m_3\\ n_1c_{23}+n_2s_{23}=n_3 m1c23+m2s23=m3n1c23+n2s23=n3
解得
x = s 23 = ( m 1 n 3 − m 3 n 1 ) / ( m 1 n 2 − m 2 n 1 ) y = c 23 = − ( m 2 n 3 − m 3 n 2 ) / m 1 n 2 − m 2 n 1 ) x=s_{23}=(m_1n_3-m_3n_1)/(m_1n_2-m_2n_1)\\ y=c_{23}=-(m_2n_3-m_3n_2)/m_1n_2-m_2n_1) x=s23=(m1n3−m3n1)/(m1n2−m2n1)y=c23=−(m2n3−m3n2)/m1n2−m2n1)
于是
θ 23 = A t a n 2 ( y , x ) \theta_{23}=\mathrm{Atan2}(y,x) θ23=Atan2(y,x)
然后再根据 θ 3 \theta_3 θ3的取值得到 θ 2 \theta_2 θ2
【!!??】起来没问题,但是算出来的结果却和预设的值不同,不知道是哪里出了问题,如果有大佬看出来了希望能指点一二。
- matlab代码实现
m1=cos(theta1)*px+sin(theta1)*py-a1;
m2=pz-d1;
m3=a3+a2*cos(theta3);
n1=-cos(theta1)*py-sin(theta1)*px+pz-d1;
n2=a1;
n3=-d4-a2*sin(theta1);
x = (m1*n3 - m3*n1)/(m1*n2 - m2*n1);
y = -(m2*n3 - m3*n2)/(m1*n2 - m2*n1);
theta23=atan2(y,x)-pi/2;%这里减pi/2因为在DH参数中theta2补偿了pi/2
· 参考的文章中的方法(失败的尝试)
也就是前面提到的这篇文章:
这篇文章中作者没有给出具体的推导过程,只给了matlab代码,代码如下
%theta2
c3=cosd(Theta3);s3=sind(Theta3);
g1=f2-d6*f1;
g2=f3-d6*az;
g3=a4*c3-d4*s3+a3;
Theta2=(atan2(g3,sqrt(g1^2+g2^2-g3^2))-atan2(g2,g1))*180/pi;
————————————————
版权声明:本文为CSDN博主「Vittore-Li」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/Vittore_Li/article/details/123185721
【!】注意,这篇文章作者的DH参数的定义和我是不一样的,我的a1=他的a2,我的a2=他的a3,我的a3=他的a4,另外他的DH模型的连杆的Z轴和我的方向是相反的,不知道会在求解中有什么影响。
我看了半天没看明白这是怎么来的,然后直接运行得到的结果也不正确(在针对我的DH模型做了相应修改后运行的)。
如果有哪个大佬知道作者用的是什么方法希望不吝赐教!(抱拳)
· 一个大佬的论文的方法(可以得到正确结果的方法)
是的,就是我前面(上一篇)说的那个大佬的论文,其实我前面的过程基本(或者说全部)也是按照大佬的步骤写的,只是加上了我的理解和验证过程。
大佬就是不一样,用的方法都是我没见过的。。。
机器人末端位置(坐标系6的原点)如下:
p x = a 1 c 1 + a 3 c 1 c 23 + d 4 c 1 s 23 + a 2 c 1 c 2 p y = a 1 s 1 + a 3 s 1 c 23 + d 4 s 1 s 23 + a 2 c 2 s 1 p z = d 1 + a 2 s 2 + a 3 s 23 − d 4 c 23 p_x=a_1c_1+a_3c_1c_{23}+d_4c_1s_{23}+a_2c_1c_2\\ p_y=a_1s_1+a_3s_1c_{23}+d_4s_1s_{23}+a_2c_2s_1\\ p_z=d_1+a_2s_2+a_3s_{23}-d_4c_{23} px=a1c1+a3c1c23+d4c1s23+a2c1c2py=a1s1+a3s1c23+d4s1s23+a2c2s1pz=d1+a2s2+a3s23−d4c23
整理可得:
p x c 1 − a 1 = a 3 c 23 + d 4 s 23 + a 2 c 2 p y s 1 − a 1 = a 3 c 23 + d 4 s 23 + a 2 c 2 p z − d 1 = a 2 s 2 + a 3 s 23 − d 4 c 23 \frac{p_x}{c_1}-a_1=a_3c_{23}+d_4s_{23}+a_2c_2\\ \frac{p_y}{s_1}-a_1=a_3c_{23}+d_4s_{23}+a_2c_2\\ p_z-d_1=a_2s_2+a_3s_{23}-d_4c_{23} c1px−a1=a3c23+d4s23+a2c2s1py−a1=a3c23+d4s23+a2c2pz−d1=a2s2+a3s23−d4c23
记
k 1 = p x c 1 − a 1 k 2 = p z − d 1 k_1=\frac{p_x}{c_1}-a_1 {k_2=p}_z-d_1 k1=c1px−a1k2=pz−d1
得到:
k 1 − a 2 c 2 = a 3 c 23 + d 4 s 23 k 2 − a 2 s 2 = a 3 s 23 − d 4 c 23 k_1-a_2c_2=a_3c_{23}+d_4s_{23}\\ k_2-a_2s_2=a_3s_{23}-d_4c_{23} k1−a2c2=a3c23+d4s23k2−a2s2=a3s23−d4c23
求平方和:
a 3 2 + d 4 2 = k 1 2 + k 2 2 + a 2 2 − 2 k 1 a 2 c 2 − 2 k 2 a 2 s 2 a_3^2+d_4^2=k_1^2+k_2^2+a_2^2-2k_1a_2c_2-2k_2a_2s_2 a32+d42=k12+k22+a22−2k1a2c2−2k2a2s2
记
k 3 = ( k 1 2 + k 2 2 + a 2 2 − a 3 2 − d 4 2 ) / 2 a 2 k_3=\left(k_1^2+k_2^2+a_2^2-a_3^2-d_4^2\right)/2a_2 k3=(k12+k22+a22−a32−d42)/2a2
则:
k 1 c 2 + k 2 s 2 = k 3 k_1c_2+k_2s_2=k_3 k1c2+k2s2=k3
解得:
θ 2 = A t a n 2 ( k 3 , ± k 1 2 + k 2 2 − k 3 2 ) − A t a n 2 ( k 1 , k 2 ) \theta_2=\mathrm{Atan2}\left(k_3,\pm\sqrt{k_1^2+k_2^2-k_3^2}\right)-\mathrm{Atan2}\left(k_1,k_2\right) θ2=Atan2(k3,±k12+k22−k32)−Atan2(k1,k2)
- matlab代码实现
k1=px/cos(theta1)-a1;
k2=pz-d1;
k3=(k1^2+k2^2+a2^2-a3^2-d4^2)/(2*a2);
theta2_1=atan2(k3,sqrt(k1^2+k2^2-k3^2))-atan2(k1,k2);
theta2_2=atan2(k3,-sqrt(k1^2+k2^2-k3^2))-atan2(k1,k2);
记得减去 θ 2 \theta_2 θ2的偏移量pi/2
❤ 2023.6.21 ❤
以上就是用代数解的方法求前三个轴的角度,按照一般流程,这个时候应该求后四个轴了,但是作为一篇总结方法型的文章,我是不满足于只记录一种实现方法的。
在学习了师弟的方法之后,我觉得用集合法解前三个轴应该是更简单的,至少和脑筋急转弯一样的代数法相比更好理解。
△ 几何解求 θ 1 \theta_1 θ1、 θ 2 \theta_2 θ2、 θ 3 \theta_3 θ3
○ 求解 θ 1 \theta_1 θ1
由机器人示意图可知,此构型的机器人,杆1、杆2、杆3组成的机构在同一竖直平面内,同时机器人末端为杆4、杆5、杆6坐标系的共同原点。由此可知,已知机器人末端坐标 ( p x , p y , p z ) \left(p_x,p_y,p_z\right) (px,py,pz)即可求得轴1的转角 θ 1 \theta_1 θ1
θ 1 = A t a n 2 ( p y , p x ) \theta_1=\mathrm{Atan2}\left(p_y,p_x\right) θ1=Atan2(py,px)
甚至不用考虑多解的情况
○ 求解 θ 3 \theta_3 θ3
机器人结构示意图如下
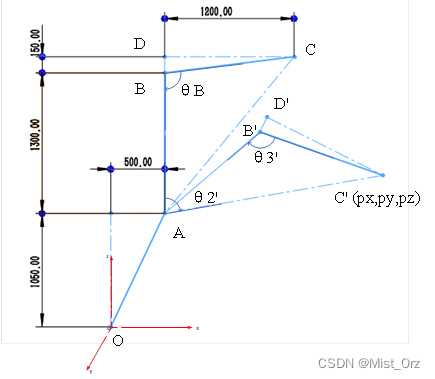
如图,C’点坐标 ( p x , p y , p z ) \left(p_x,p_y,p_z\right) (px,py,pz),A点坐标 ( a 1 cos θ 1 , a 1 sin θ 1 , d 1 ) \left(a_1\cos{\theta_1},a_1\sin{\theta_1},d_1\right) (a1cosθ1,a1sinθ1,d1)
L B ′ C ′ = L B C = B D 2 + C D 2 = a 3 2 + d 4 2 L A C = A D 2 − C D 2 = ( a 2 + a 3 ) 2 − d 4 2 L A B ′ = L A B = a 2 L_{B^\prime C^\prime}=L_{BC}=\sqrt{BD^2+CD^2}=\sqrt{a_3^2+d_4^2}\\ L_{AC}=\sqrt{AD^2-CD^2}=\sqrt{\left(a_2+a_3\right)^2-d_4^2}\\ L_{AB^\prime}=L_{AB}=a_2 LB′C′=LBC=BD2+CD2=a32+d42LAC=AD2−CD2=(a2+a3)2−d42LAB′=LAB=a2
因为点O,A,C’共平面,所以
L A C ′ = ( p x 2 + p y 2 − a 1 ) 2 + ( p z − d 1 ) 2 L_{AC^\prime}=\sqrt{\left(\sqrt{p_x^2+p_y^2}-a_1\right)^2+\left(p_z-d_1\right)^2} LAC′=(px2+py2−a1)2+(pz−d1)2
根据余弦定理:
c 2 = a 2 + b 2 − 2 a b cos γ c^2=a^2+b^2-2ab\cos{\gamma} c2=a2+b2−2abcosγ
得,在 Δ A B ′ C ′ \Delta A\mathrm{B}^\mathrm{'}\mathrm{C}^\mathrm{'} ΔAB′C′中:
cos θ 3 ′ = L A B ′ 2 + L B ′ C ′ 2 − L A C ′ 2 2 L A B ′ L B ′ C ′ \cos{\theta_3^\prime}=\frac{L_{AB^\prime}^2+L_{B^\prime C^\prime}^2-L_{AC^\prime}^2}{2L_{AB^\prime}L_{B^\prime C^\prime}} cosθ3′=2LAB′LB′C′LAB′2+LB′C′2−LAC′2
同样由余弦定理得,在 Δ A B C \Delta ABC ΔABC中:
cos θ B = L A B 2 + L B C 2 − L A C 2 2 L A B L B C \cos{\theta_B}=\frac{L_{AB}^2+L_{BC}^2-L_{AC}^2}{2L_{AB}L_{BC}} cosθB=2LABLBCLAB2+LBC2−LAC2
根据几何关系可得:
θ 3 = arccos θ 3 ′ − arccos θ B \theta_3=\arccos{\theta_3^\prime}-\arccos{\theta_B} θ3=arccosθ3′−arccosθB
注意根据余弦定理的性质,得到的 θ 3 ′ \theta_3^\prime θ3′的值始终小于180°,而 θ 3 + θ B \theta_3+\theta_B θ3+θB存在大于180°的情况,所以 θ 3 \theta_3 θ3的取值有两组。
○ 求解 θ 2 \theta_2 θ2
根据 θ 2 \theta_2 θ2与 θ 3 \theta_3 θ3取值情况的不同, θ 2 \theta_2 θ2的解有如下四种情况:
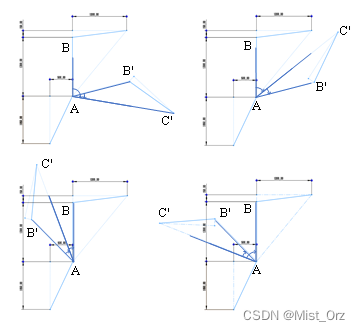
θ 2 = ∠ B A C ′ − ∠ B ′ A C ′ θ 2 = ∠ B A C ′ + ∠ B ′ A C ′ θ 2 = − ∠ B A C ′ − ∠ B ′ A C ′ θ 2 = − ∠ B A C ′ + ∠ B ′ A C ′ \theta_2=\angle\mathrm{BA}\mathrm{C}^\mathrm{'}-\angle\mathrm{B}^\mathrm{'}\mathrm{AC}^\mathrm{'}\\ \theta_2=\angle\mathrm{BA}\mathrm{C}^\mathrm{'}+\angle\mathrm{B}^\mathrm{'}\mathrm{AC}^\mathrm{'}\\ \theta_2=-\angle\mathrm{BA}\mathrm{C}^\mathrm{'}-\angle\mathrm{B}^\mathrm{'}{\mathrm{AC}}^\mathrm{'}\\ \theta_2=-\angle\mathrm{BA}\mathrm{C}^\mathrm{'}+\angle\mathrm{B}^\mathrm{'}\mathrm{AC}^\mathrm{'} θ2=∠BAC′−∠B′AC′θ2=∠BAC′+∠B′AC′θ2=−∠BAC′−∠B′AC′θ2=−∠BAC′+∠B′AC′
根据图-可得,B点坐标 ( a 1 cos θ 1 , a 1 sin θ 1 , d 1 + a 2 ) \left(a_1\cos{\theta_1},a_1\sin{\theta_1},d_1+a_2\right) (a1cosθ1,a1sinθ1,d1+a2)。
因为点O,A,B,C’共平面,所以
L B C ′ = ( p x 2 + p y 2 − a 1 ) 2 + ( p z − d 1 − a 2 ) 2 L_{BC'}=\sqrt{\left(\sqrt{p_x^2+p_y^2}-a_1\right)^2+\left(p_z-d_1-a_2\right)^2} LBC′=(px2+py2−a1)2+(pz−d1−a2)2
设 ∠ B A C ′ = β \angle\mathrm{BA}\mathrm{C}^\mathrm{'}=\beta ∠BAC′=β, ∠ B ′ A C ′ = γ \angle\mathrm{B}^\mathrm{'}\mathrm{AC}^\mathrm{'}=γ ∠B′AC′=γ
根据余弦定理,在 Δ A B C ′ \Delta \mathrm{ABC}^\mathrm{'} ΔABC′中:
cos β = L A B 2 + L A C ′ 2 − L B C ′ 2 2 L A B L A C ′ \cos{\beta}=\frac{L_{AB}^2+L_{AC^\prime}^2-L_{BC^\prime}^2}{2L_{AB}L_{AC^\prime}} cosβ=2LABLAC′LAB2+LAC′2−LBC′2
在 Δ A B ′ C ′ \Delta \mathrm{AB}^\mathrm{'}\mathrm{C}^\mathrm{'} ΔAB′C′中:
cos γ = L A B ′ 2 + L A C ′ 2 − L B ′ C ′ 2 2 L A B ′ L A C ′ \cos{\gamma}=\frac{L_{AB^\prime}^2+L_{AC^\prime}^2-L_{B^\prime C^\prime}^2}{2L_{AB^\prime}L_{AC^\prime}} cosγ=2LAB′LAC′LAB′2+LAC′2−LB′C′2
根据式()可得:
θ 2 = ± arccos β ± arccos γ \theta_2=\pm\arccos{\beta}\pm\arccos{\gamma} θ2=±arccosβ±arccosγ
θ 2 \theta_2 θ2可得到四组解。
○ 几何法总结
在整理完几何法求前三轴角度的方法之后,我觉得几何法也不是那么的简单,但是直观是肯定的,然而几何解并没有改善代数解得多解的情况,并且这个多解需要根据几何关系来进行判断,不一定就比代数解更简单。
因为计算过程并不复杂,这里就不给出matlab的代码了(主要我也没敲)。
如果过程有什么问题或者有更优的方法还请各位大佬赐教!(抱拳)
△ 代数解求 θ 4 \theta_4 θ4、 θ 5 \theta_5 θ5、 θ 6 \theta_6 θ6
CSDN又提示我字数太多,一篇发不下,只好拆开,逆运动学求解 θ 4 \theta_4 θ4、 θ 5 \theta_5 θ5、 θ 6 \theta_6 θ6,雅克比相关的内容见
