PCA(Principal Component Analysis)
一、对 PCA 的理解
- 名称:主成分分析算法;
- 类型:非监督机器学习算法;
- 主要功能:主要用于数据的降维;
- 其它应用:数据可视化、去燥;
- 不仅在机器学习领域应用,也是统计学领域的重要应用
- 数据降维的意义
- 从数据中发现更便于人类理解的特征;
- 方便数据可视化,使人类更容易理解可视化后的数据;
- 提高算法的运行效率;
- 有时,数据经过主成分分析以后再用于机器学习算法,数据的被识别率更好;
二、降维
- 注:
- 降维的目的:优化数据集;
- 得到优化的数据集的前提:得到最佳的降维空间;
- 得到最佳的降维空间的条件:降维后的数据集的方差最大;
- 使方差最大的优化方法:梯度上升法;
1)实例说明数据的降维
- 二维特征空间的样本点

- 方案(一):抛除特征一,降维后的特征关系

- 方案(二):抛除特征二,降维后的数据关系
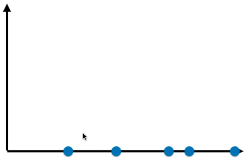
- 两种降维方案,方案(二)更好:
- 方案(二)降维后的样本点映射到坐标轴上,点与点之间的距离较大,说明样本点之间具有较高的可区分度;
- 更好的保持了原来的点与点(二维特征空间里的样本点)之间的距离;
2)PCA 方法降维
- 疑问:有没有更好的降维方案?
- 什么叫更好:使样本的区分度更加明显
- 方案(三)
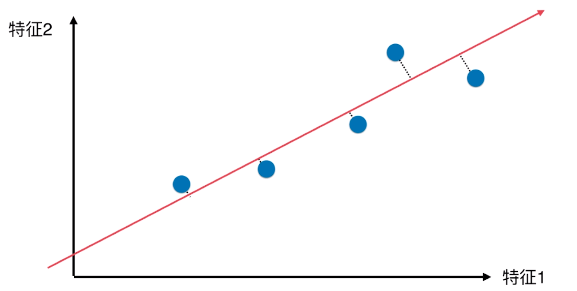
- 降维后的样本点分布
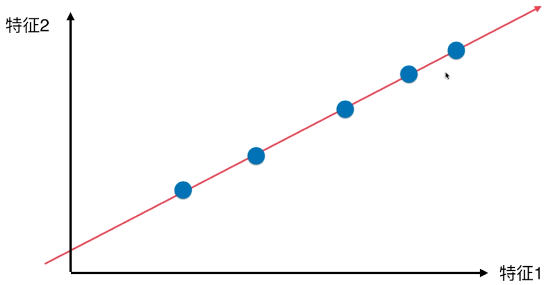
- 优点:
- 所有的样本点的差异(或者距离),更趋近原来二维特征空间内样本点的差异(或距离);
- 与方案(一)、方案(二)相比,样本的区分度更加明显;
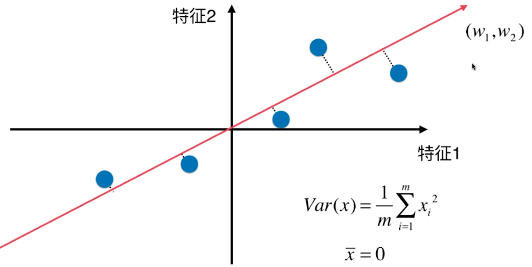
3)降维后的特征空间(w)
- 最佳的降维特征空间满足的条件:映射到降维特征空间后的数据集的方差最大时,对应的降维空间最佳;
1、分析
- 问题(一):怎么找到这样的一条直线?(让降维后的样本间间距最大)
- 在二维特征空间中,这条直线就是降维后的特征空间;
- 问题(二):如何定义样本间间距?
- 方案:使用方差(Variance)表示样本间的距离;
- 方差:描述样本(数据)在空间内(可以是一维、二维、多维空间)分布疏密的指标,方差越大,样本之间越稀疏;方差越小,样本之间越紧密;
- 方差公式:
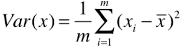 ;
; - xi:m 个数据中的第 i 个数据;
2、二维特征空间降维成一维特征空间
- 思路:找到一个轴,得到样本空间的所有点映射到这个轴后,方差最大(表示样本间间距越大);
- 具体操作步骤:
A、第一步:将每一种特征的均值归为 0 (此过程称为 demean)
# 样本分布没变,移动坐标轴位置,得到样本在每一个维度的均值都为 0 ;(见下图)
# 公式变形: ,均值
,均值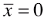 ;
;
# Xi :值映射到新的坐标轴上之后,得到的新的样本;
B、第二步:求一个轴的方向 w = (w1 , w2),使得所有的样本映射到 w 以后,有: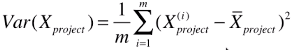 最大;
最大;
# 公式变形后:![]()
- Var(Xproject):映射后的样本的方差;
- Xpreject(i):映射后的样本,在特征空间中,也可以看做是一个向量;
- || Xpreject(i) ||:映射后的样本向量的模;
# 注:此直线,不是线性回归的线性模型直线,本例只是简化为对二维空间内的只有两个特征的样本数据进行降维;
# 而线性回归中,是样本的 n 维特征和样本对应的输出值之间的关系
# 怎么得到 Xpreject ?
# 1)映射过程:就是一个向量投影到另一个向量上
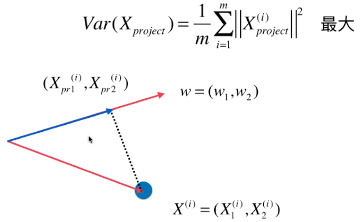
- w = (w1, w2):特征空间中,目标轴的方向;
- X(i):特征空间中,数据集的第 i 个样本;
- X(i) = ( X1(i), X2(i) ):特征空间中,样本点也可以看做一个向量;
- (Xpr1(i), Xpr2(i)):映射后的样本点的特征值;
# 2)计算映射后的样本特征
# 其实就是向量之间的运算;
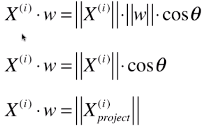
- θ:两向量的夹角;
# 最终公式变形: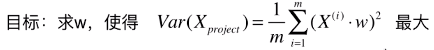 ;
;
- 此公式是针对本例中的两个特征的样本
# 推广到 n 为空间(一个样本有 n 个特征):
# 变形公式: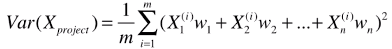
# 再次变形,得最终公式: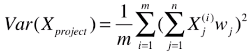
# 以本例分析:
# 1)降维的目的:优化数据;
# 2)降维的手段:找到一条
# 3)优化结果:得到新的数据集 Xpreject ;
# 降维的实现手段,转变为:优化目标函数,使得其最大时对应的