机器学习实战——PCA降维

• Dimensionality reduction techniques降维
  • 降维是对数据高维度特征的一种预处理方法。降维是将高维度的数据保留下最重要的一些特征，去除噪声和不重要的特征，从而实现提升数据处理速度的目的
  • 降维在一定的信息损失范围内，可以为我们节省大量的时间和成本。降维也成为了应用非常广泛的数据预处理方法。

1 降维技术

• 我们希望简化数据：
  • 使数据集更易于使用
  • 降低算法的计算成本
  • 消除噪音
  • 使结果更易于理解
• 降维分类：
  • 主成分分析
  • 因素分析
  • 独立分量分析（ICA）

2 PCA

• PCA(principal Component Analysis)，即主成分分析方法，是一种使用最广泛的数据压缩算法

  • 优点：降低数据的复杂性，识别最重要的多个特征。
  • 缺点：不一定需要，且可能损失有用信息。适用数据类型：数值型数据。
  • 在PCA中，数据从原来的坐标系转换到新的坐标系new coordinate system，由数据本身决定。
  • 转换坐标系时，以方差最大的方向作为坐标轴方向the direction of the most variance in the data，因为数据的最大方差给出了数据的最重要的信息。
  • 第一个新坐标轴选择的是原始数据中方差最大的方法，第二个新坐标轴选择的是与第一个新坐标轴正交且方差次大的方向。重复该过程，重复次数为原始数据的特征维数。
  • 通过这种方式获得的新的坐标系，大部分方差都包含在前面几个坐标轴中，后面的坐标轴所含的方差几乎为0，我们可以忽略余下的坐标轴，只保留前面的几个含有绝大部分方差的坐标轴$\to$这样也就相当于只保留包含绝大部分方差的维度特征，而忽略包含方差几乎为0的特征维度，也就实现了对数据特征的降维处理

• 事实上，通过计算数据矩阵的协方差矩阵，然后得到协方差矩阵的特征值及特征向量，选择特征值最大（也即包含方差最大）的N个特征所对应的特征向量组成的矩阵$\to$就可以将数据矩阵转换到新的空间当中，实现数据特征的降维（N维）

• 一种直观的看法是：希望投影后的的投影值尽可能分散$\to$可以用数学上的方差来表述
  $$V_{ar}(a)=\frac{1}{m}\sum _{i=1}^m(a_i-\mu {)}^2$$

• 对于上面二维降成一维的问题来说，找到那个使得方差最大的方向就可以了

• 对于更高维:例如考虑三维降到二维问题

  • 与之前相同，首先我们希望找到一个方向使得投影后方差最大，这样就完成了第一个方向的选择，继而我们选择第二个投影方向
  • 如果我们还是单纯只选择方差最大的方向，很明显，这个方向与第一个方向应该是“几乎重合在一起”，显然这样的维度是没有用的，因此，应该有其他约束条件。
  • 从直观上说，尽可能表示更多的原始信息，我们是不希望它们之间存在（线性）相关性的，因为相关性意味着两个成分不是完全独立，必然存在重复表示的信息
  • 数学上可以用两个成分的协方差表示其相关性
  • 当协方差为0时，表示两个成分完全独立。为了让协方差为0，我们选择第二个新坐标轴时只能在与第一个新坐标轴正交的方向上选择

2.1 移动坐标轴

考虑下图中的大量数据点。如果要求我们画出一条直线，这条线要尽可能覆盖这些点，那么最长的线可能是哪条？

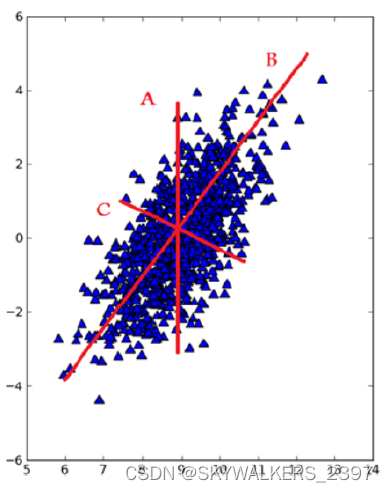
3条直线中B最长。在PCA中,我们对数据的坐标进行了旋转，该旋转的过程取决于数据的本身。第一条坐标轴旋转到覆盖数据的最大方差位置，即图中的直线B。数据的最大方差给出了数据的最重要的信息。假如该坐标轴与第一条坐标轴垂直，它就是覆盖数据次大差异性的坐标轴。这里更严谨的说法就是正交(orthogonal) ，直线C就是第二条坐标轴。

PCA的基本过程：

• 第一个主成分就是从数据差异性最大（即方差最大）的方向提取出来的
• 第二个主成分则来自于数据差异性次大的方向，并且该方向与第一个主成分方向正交。
• 通过数据集的协方差矩阵及其特征值分析，我们就可以求得这些主成分的值。一旦得到了协方差矩阵的特征向量，我们就可以保留最大的N个值。
• 这些特征向量也给出了个最重要特征的真实结构。我们可以通过将数据乘上这N个特征向量而将它转换到新的空间

2.2 在NumPy中实现PCA

伪代码

去除平均值
计算协方差矩阵
计算协方差矩阵的特征值和特征向量
将特征值从大到小排序
保留最上面的N个特征向量
将数据转换到上述N个特征向量构建的新空间中

python代码

def pca(dataMat, topNfeat=9999999):
    meanVals = np.mean(dataMat, axis=0)  # 计算平均值
    meanRemoved = dataMat - meanVals  # 去中心化
    covMat = np.cov(meanRemoved, rowvar=False)  # 计算协方差矩阵
    eigVals, eigVects = np.linalg.eig(np.mat(covMat))  # 得到所有的特征值eigVals和特征向量eigVects

    sum_eig = sum(eigVals)
    percentVar = eigVals / sum_eig
    cumVarPercent = 0.0
    print('自编python代码：')
    for i in range(topNfeat):
        cumVarPercent += percentVar[i]
        print("第%d个主成分所占的方差百分比：%f,累计方差百分比:%f" % (i + 1, percentVar[i], cumVarPercent))

    plt.plot(range(30), percentVar[:30])  # 绘图
    x_major_locator = MultipleLocator(1)  # 把x轴的刻度间隔设置为1，并存在变量里
    ax = plt.gca()  # ax为两条坐标轴的实例
    ax.xaxis.set_major_locator(x_major_locator)  # 把x轴的主刻度设置为1的倍数
    plt.xlim(-0.5, 30)
    plt.rcParams['font.sans-serif'] = ['SimHei']
    plt.xlabel("主成分数目")
    plt.ylabel("方差百分比")
    plt.title('不同主成分下的方差百分比')
    eigValInd = np.argsort(eigVals)  # 排序
    eigValInd = eigValInd[:-(topNfeat + 1):-1]  # 保留至想要的维度
    redEigVects = eigVects[:, eigValInd]  # 从大到小排列特征向量，得到投影矩阵
    lowDataMat = meanRemoved * redEigVects  # 投影到新的特征空间后的数据集
    reconMat = (lowDataMat * redEigVects.T) + meanVals  # 重构矩阵，即得出降维后矩阵在原维度下是什么样的，便于比较
    return lowDataMat, reconMat

3 示例：利用PCA对半导体制造数据降维

读取数据：

def loadDataSet(fileName, delim='\t'):
    dataArr = pd.read_csv('secom.data', sep=' ', names=[i for i in range(590)])  # 添加列索引，防止把第一列当成列索引
    # dataArr = np.array(dataArr)
    print(dataArr)
    return np.mat(dataArr)

数据包含很多的缺失值NaN (Not a Number）$\to$用平均值来代替缺失值，平均值根据那些非NAN得到。

def replaceNanWithMean():
    dataMat = loadDataSet('secom.data', '')
    numFeat = np.shape(dataMat)[1]
    for i in range(numFeat):
        meanVal = np.mean(dataMat[np.nonzero(~np.isnan(dataMat[:, i].A))[0], i])
        dataMat[np.nonzero(np.isnan(dataMat[:, i].A))[0], i] = meanVal
    return dataMat

4 总结

• 降维技术使得数据变得更易使用，并且它们往往能够去除数据中的噪声，使得其他机器学习任务更加精确。
• 降维往往作为预处理步骤，在数据应用到其他算法之前清洗数据。
• 数据降维技术中，独立成分分析、因子分析和主成分分析比较流行，其中又以主成分分析应用最广泛。