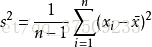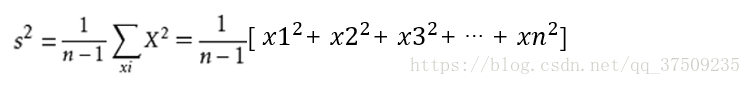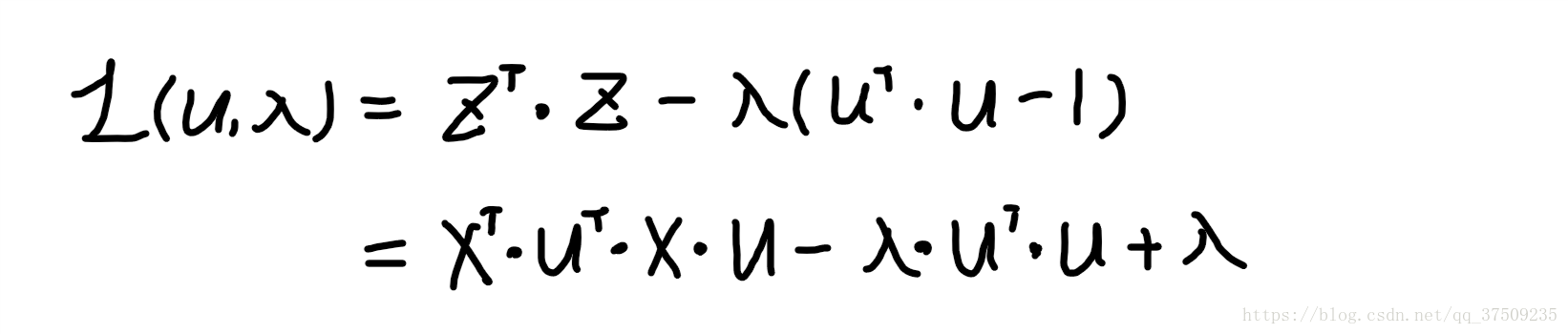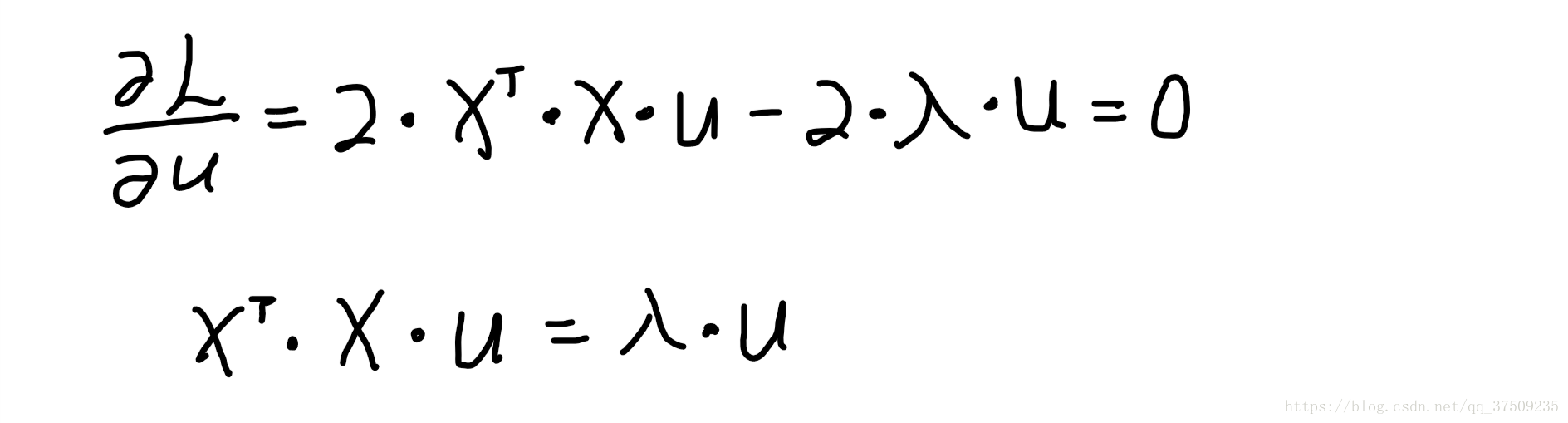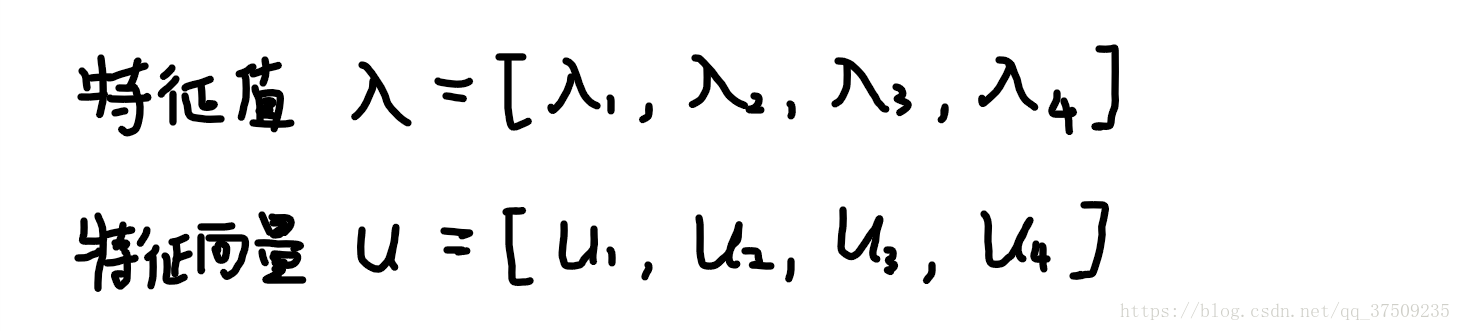机器学习之主成分分析PCA（降维）

理解PCA：what? why? how?

当我们拿到一个数据集的时候，往往数据集中每一个样本的描述是多维的

例如鸢尾花数据集：http://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data
数据集中对150个鸢尾花样本的描述：萼片长度，萼片宽度，花瓣长度，花瓣宽度
当我们读取数据时会读到一个 150x4 的矩阵 X(150x4)，但是四维的特征空间不便于我们或者计算机对其进行分析和处理，所以我们希望用低维度的特征向量来表述样本的特征，此时我们需要对其进行降维

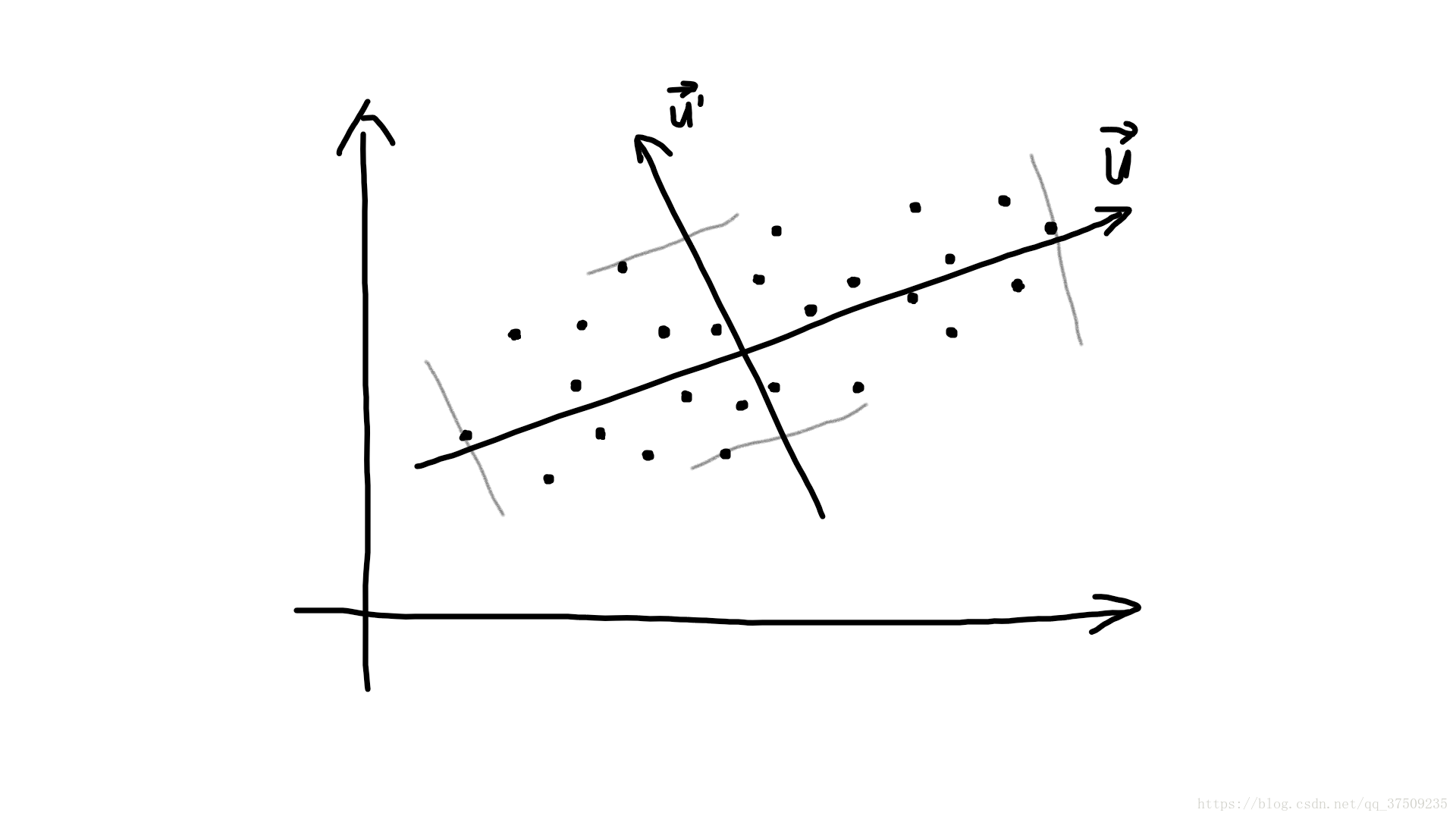
假设矩阵 X 在多维空间中有 n 个样本点：

我们希望它们投影到一个方向 u 上，使得投影范围最大，这个方向称为主方向（主成分PCA），可以用方差度量一个随机变量离散程度，即可用方差度量样本点在一个方向上投影之后得离散程度

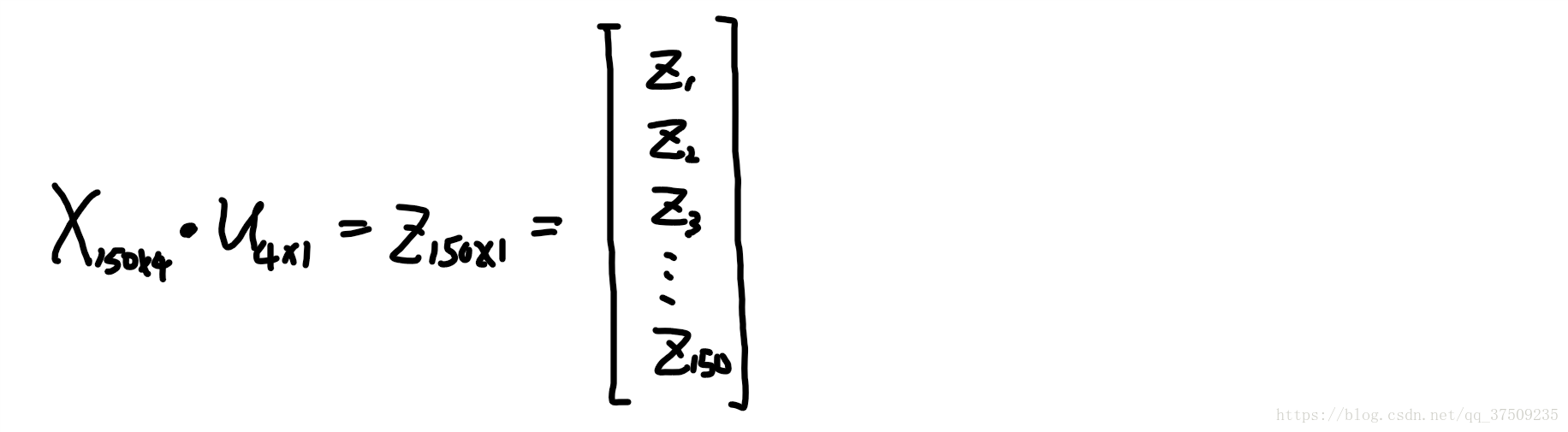
样本 X(150x4) 投影到 u(4x1) 方向上，即 X•u，得到一个一维的向量 Z(150x1)

对 Z 求方差，而使得方差最大的那个 u 就是主方向，所以我们需要对z = X•u求方差，并且求方差的极值

一、求方差：

中心化后的x的均值为0，所以求方差可简化为：

线性代数表示方差 z^T•z = [ z1² + z2² + z3² + … + zn² ] ，z = X•u

二、拉格朗日乘子法求 z^T•z 极值（方差最大值）

u 是单位向量，约束条件为：u^T•u = 1， 即 u^T•u - 1 = 0

根据线形代数定理：(X^T•A•X)’ = 2•A•X ， 则L(u, λ) 对 u 求偏导得：

X^T 是 4x150 矩阵，X 是150x4的矩阵，则式子中 X^T•T 是4x4的矩阵，对 X^T•T 求得特征值 λ 和特征向量 u

而最大特征值 λ 所对应的 u 就是主方向！

PCA就是样本投影之后方差最大的方向即主方向
次方向就是垂直于主方向的剩下的最大的 λ 所对应的 u …
（特征向量 u 中的所有方向互相垂直）

前k个主方向的选取：

有时候降到一维（只选取一个主方向）并不是最优，所以我们可以选取 k 个主方向
对λ和u排序，计算 (λ1+λ2+λ3+λ4)x85% 得到一个值 w
如果发现前k个λ的和大于 w 就选取对应k个u作为前k个主向量
(85%只是一个可接受的能量比例）
反过来选取k个主方向，算出掌握多大能量和损失多大能量

降维具有如下优点：

1. 使得数据集更易使用
2. 降低算法的计算开销
3. 去除噪声
4. 使得结果容易理解