降维：LDA与PCA的简析理解

LDA

LDA(二分类情况）

LDA是一种监督学习的降维技术，也就是说LDA依赖于样本的类别输出。LDA的基本思路就是将样本投影到一条直线上，使类间距离尽可能变大，类内距离尽可能变小。如下图所示：

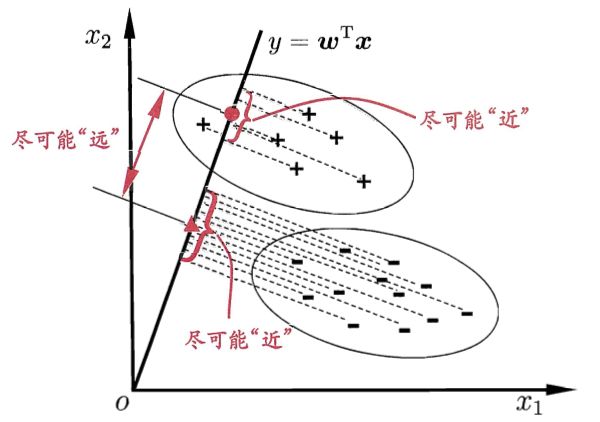
在这里插入图片描述

那么我们可以通过 $y=w^Tx$ 来计算投影，当x是二维的时候，我们就需要找到一个w来做投影，然后寻找最能使样本点分离的直线。

那么我们应该如何来找到最佳的w呢？

我们分别选择两个类别的中心点 $\mu_0,\mu_1$ ,那么经过投影之后可以得到 $w^T\mu_0$ 和 $w^T\mu_1$ ，分别用 $\tilde{\mu_0}$ 和 $\tilde{\mu_1}$ 来表示。

我们首先会想到使两个类别的中心点尽量分离，定量表示为：
$arg\ max_w j(w)=||w^T\mu_0-w^T\mu_1||_2^2=||\tilde{\mu_0}-\tilde{\mu_1}||_2^2$
但是同时我们考虑到上述表示只能让类间差距变大，而无法使类内差距变小，因此我们又会想到度量类内的差距：
$\tilde{S}^2=\sum_{x\in X_i}(w^Tx-\tilde{\mu_i})$
很明显，针对我们二分类的情况来说，我们需要分别计算两个类内差距并求和得到总的差距度量。
$min\ \tilde{S_0}^2+\tilde{S_1}^2$
为了让上述分析的两个条件有效的合并，则可得出：
$J(w)=\frac{||w^T\mu_0-w^T\mu_1||_2^2}{\tilde{S_0}^2+\tilde{S_1}^2}$
那么现在很明显我们只需要优化上式即可，得到我们所需的w。

首先我们将 $\tilde{S}^2=\sum_{x\in X_i}(w^Tx-\tilde{\mu_i})=\sum_{x\in X_i}w^T(x-\mu_i)(x-\mu_i)^Tw$

然后我们对上式的中间部分给出定义：
$\sum_i=\sum_{x\in X_i}(x-\mu_i)(x-\mu_i)^T$
那么我们又可以给出定义：
$S_w=\sum_0+\sum_1$
同时我们可以将 $||w^T\mu_0-w^T\mu_1||_2^2$ 展开得到：
$w^T(\mu_0-\mu_1)(\mu_0-\mu_1)^Tw$
同样的，我们对中间部分给出定义：
$S_b=(\mu_0-\mu_1)(\mu_0-\mu_1)^T$
那么我们之前定义的 $J(w)$ 可以定义为：
$J(w)=\frac{w^TS_bw}{w^TS_w w}$
这就是LDA欲最大化的目标。即 $S_b$ 与 $S_w$ 的“广义瑞利商“（generalized Rayleigh quotient）

利用拉格朗日乘子法求解:
$min_w -w^TS_bw \\ s.t.\ \ w^TS_ww=1$
可得：
$c(w)=-w^TS_bw+\lambda(w^TS_ww-1)\\ \rightarrow \frac{dc}{dw}=-2S_bw+2\lambda S_ww=0 \\ \rightarrow S_bw=\lambda S_ww$

由于 $S_bw$ 的方向恒为 $\mu_0-\mu_1$ ,不妨令：
$S_bw=\lambda(\mu_0-\mu_1)$
将其带入上式得：
$w=S_w^{-1}(\mu_0-\mu_1)$

多分类情况

$S_w=\sum^c_{i=1}S_{w_i}$
$S_b$ 需要变，原来度量的是两个均值点的散列情况，现在度量的每个均值点相对于样本中心的散列情况。如图所示：

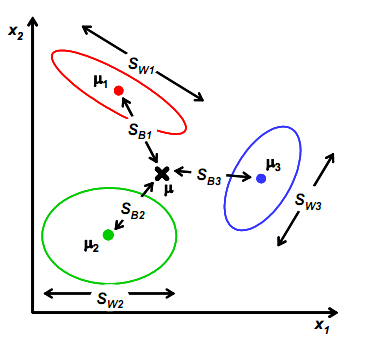
在这里插入图片描述

类似将 $\mu_i$ 看作样本点， $\mu$ 是均值的协方差矩阵，如果某类里面的样本点较多，那么可能权重要稍大，即使用 $\frac{N_i}{N}$ 表示，但由于J(w)对倍数不敏感，因此使用 $N_i$ 。
$S_b=\sum_{i=1}^cN_i(\mu_i-\mu)(\mu_i-\mu)^T$
同理还是求解：
$S_bw=\lambda S_ww$

小结

LDA算法既可以用来降维，又可以用来分类，但是目前来说，主要还是用于降维。下面总结下LDA算法的优缺点。

LDA算法的主要优点有：

在降维过程中可以使用类别的先验知识经验，而像PCA这样的无监督学习则无法使用类别先验知识。
LDA在样本分类信息依赖均值而不是方差的时候，比PCA之类的算法较优。

LDA算法的主要缺点有：

LDA不适合对非高斯分布样本进行降维，PCA也有这个问题。
LDA降维最多降到类别数k-1的维数，如果我们降维的维度大于k-1，则不能使用LDA。当然目前有一些LDA的进化版算法可以绕过这个问题。
- 具体原因是由于 $S_b$ 中的 $u_i-i$ 秩为1，因此 $S_b$ 的秩最多为C（矩阵的秩小于等于各个相加矩阵的和）。由于知道了前C-1个 $\mu_i$ 后，最后一个 $\mu_i$ 可以由前面的 $\mu_i$ 来线性表示，因此 $S_b$ 的秩最多为C-1，即特征向量最多有C-1个。
LDA在样本分类信息依赖方差而不是均值的时候，降维效果不好。
LDA可能过度拟合数据。

PCA

关于PCA的介绍，这篇博客介绍的比较简洁明了了，可直接参考。

博客链接