MATLAB——DFS离散傅里叶级数

题目：
已知一个周期性矩形序列的脉冲宽度占整个周期的1/4，一个周期的采样点为16点。用傅里叶级数求信号的幅度和相位频谱；求傅里叶级数逆变换的图形，与原信号图形进行比较。
问题分析：
经过采样之后，原来的信号变成了离散信号，时域周期造成了频域离散。所以对应的就是离散傅里叶级数。
公式：
DFS
$$X[k]=\sum _{n=0}^{N-1}x[n]e^{-j\frac{2\pi }{N}kn}$$
IDFS
$$x[n]=\frac{1}{N}\sum _{k=0}^{N-1}X[k]e^{j\frac{2\pi }{N}kn}$$
MATLAB里面只有计算快速傅里叶变换的函数fft()。所以这里我们需要自己创建函数文件，进行DFS和IDFS运算。
函数文件：

function Xk= dfs(xn,N )%定义函数，返回一个变量Xk
n=[0:1:N-1];%采样点
k=n;
WN=exp(-2*pi*j/N);
Xk=xn*(WN.^(n'*k));
end

注意：在任何使用到矩阵的运算的时候都要注意点乘以及点方 和 乘和乘方的区别，一个是矩阵运算，一个是代数运算。

这段 MATLAB 代码实现了基于矩阵计算的离散傅里叶级数（Discrete Fourier Series，DFS），将离散时间序列 $x[n]$ 转换为频域上的序列 $X[k]$。

其中，输入参数 $xn$ 表示离散时间序列，$N$ 表示序列的长度。函数的输出结果 $xk$ 表示对应的离散傅里叶级数系数。

代码中，首先生成了两个行向量 $n$ 和 $k$，分别表示时域上的时间点和频域上的频率。接着，计算了离散傅里叶变换中需要用到的 WN 因子，以及矩阵 $nk$，它是一个 $N\times N$ 的矩阵，其中第 $i$ 行第 $j$ 列的元素 $n{k}_{i,j}$ 表示 $n_i\cdot k_j$ 的值。

接下来，计算了 DFS 矩阵 $WNnk$，它也是一个 $N\times N$ 的矩阵，其中第 $i$ 行第 $j$ 列的元素 $WNn{k}_{i,j}$ 表示 $W{N}^{n_i\cdot k_j}$ 的值。最后，用离散时间序列 $x[n]$ 与 DFS 矩阵 $WNnk$ 相乘，得到了离散傅里叶级数系数 $X[k]$。
同理，也可以创建IDFS的函数文件。

function xn = idfs( Xk,N)
n=[0:1:N-1];%采样点
k=n;
WN=exp(-2*pi*j/N);
xn=(Xk*(WN.^(-(n'*k))))/N;
end

脚本文件：

N=16;%规定采样点数
n=0:N-1;
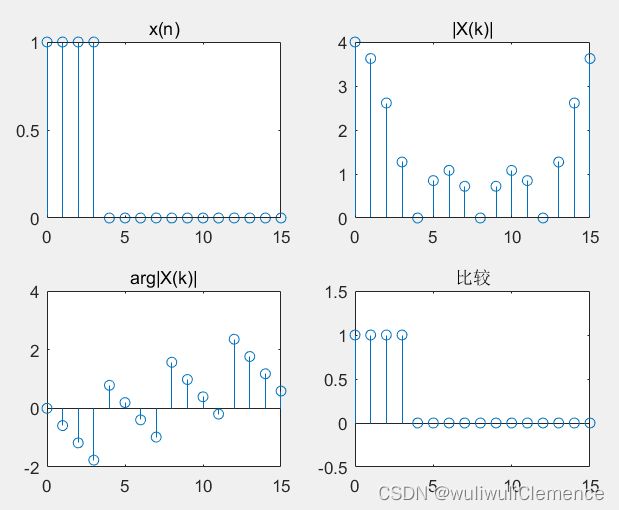
xn=[ones(1,N/4),zeros(1,3*N/4)];
subplot(2,2,1); stem(n,xn); title('x(n)');
Xk=dfs(xn,N);
subplot(2,2,2); stem(n,abs(Xk));  title('|X(k)|');
subplot(2,2,3); stem(n,angle(Xk));  title('arg|X(k)|');
xn1=idfs(Xk,N);
subplot(2,2,4); stem(n,xn1);  title('比较');

运行结果：

题目2：
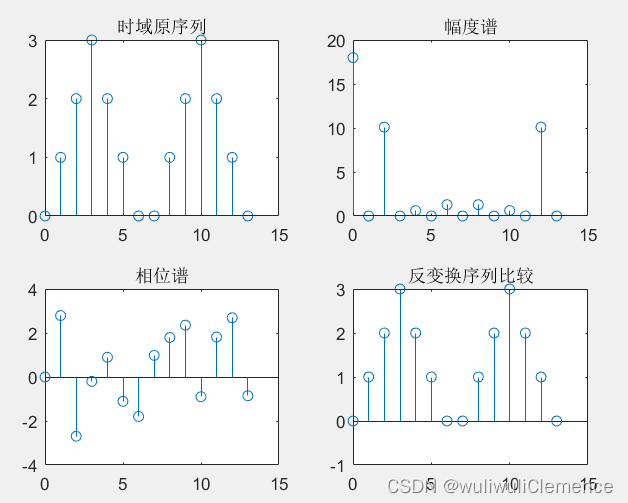
已知一个信号序列的主值为$x(n)=[0,1,2,3,2,1,0]$,显示两个周期的信号序列波形。
用傅里叶级数求信号的幅度和相位频谱；求傅里叶级数逆变换的图形，与原信号图形进行比较。
程序基本和上面一致，这里要注意的是，就是N的取值N=length（xn）。
代码：

x=[0,1,2,3,2,1,0];
x1=x'.*ones(1,2);
xn=x1(:)';
n1=0:13;
subplot(221);
stem(n1,xn);
title('时域原序列')

N=length(xn);
n=0:N-1;
Xk=dfs(xn,N);
subplot(222);
stem(n,abs(Xk));
title('幅度谱');
subplot(223);
stem(n,angle(Xk));
title('相位谱');

xn1=idfs(Xk,N);
subplot(224);
stem(n,xn1);
title('反变换序列比较');

运行结果：

题目3：
周期重复次数对序列的频谱影响
已知一个矩形序列的脉冲宽度占整个周期的1/2，一个周期的采样点数为10，用傅立叶级数变换求信号的重复周期数分别为1、4、7、10时的幅度频谱。
完整代码及其解释：

xn=[ones(1,5),zeros(1,5)]; % 定义一个信号xn，它由5个1和5个0组成
Nx=length(xn); % 获取xn的长度，Nx=10
Nw=1000;dw=2*pi/Nw; % 定义DFT点数和频率间隔
k=floor((-Nw/2+0.5):(Nw/2+0.5)); % 定义频域上的k值，使k中心在0
for r=0:3; % 对于4个不同的r值（0,1,2,3），生成4组不同的信号和它们的DFT
    K=3*r+1; % 定义K值为3r+1，它控制了信号中的周期性
    nx=0:(K*Nx-1); % 定义时间轴上的n值
    x=xn(mod(nx,Nx)+1); % 生成一个周期性信号，其周期为xn，长度为K*Nx
    Xk=x*(exp(-j*dw*nx'*k))/K; % 计算信号x的DFT，k表示频率轴上的频率值
    subplot(4,2,2*r+1); stem(nx,x) % 绘制信号x的时域波形
    axis([0,K*Nx-1,0,1.1]); ylabel('x(n)'); % 设置绘图范围和标签
    subplot(4,2,2*r+2); plot(k*dw,abs(Xk)) % 绘制信号x的频域幅度谱
    axis([-4,4,0,1.1*max(abs(Xk))]); ylabel('X(k)'); % 设置绘图范围和标签
end

重点解释：
（1）k=floor((-Nw/2+0.5):(Nw/2+0.5));
这段代码是定义一个长度为Nw的频域上的k值数组，使得k数组中心对应的频率为0，即k中心在0。具体解释如下：
Nw是DFT的点数，表示离散的频率轴上有Nw个点。通常情况下，Nw是2的幂次方，如Nw=256，512等。
dw是频率轴上两个相邻频率点之间的间隔，它的值可以通过2π/Nw计算得到。
(-Nw/2+0.5):(Nw/2+0.5)是一个长度为Nw+1的数组，包含了从-Nw/2+0.5到Nw/2+0.5的所有整数。其中0.5是为了使得k数组中心对应的频率为0，即把k轴坐标从整数值偏移0.5。
floor是一个向下取整函数，用于把k数组中的浮点数向下取整为最接近它的整数。这是为了保证k数组中的所有值都是整数，便于后续计算和绘图。中心频率设为0是为了方便表示信号在频域上的对称性，即实部和虚部分别对称。此外，因为DFT是一个离散变换，频率轴上的点数有限，因此我们需要从有限的采样点中尽可能精确地表示信号的频率成分，以尽可能减小采样误差。因此，频率轴上的采样点需要尽可能密集地分布。但是，在DFT中，频率轴上的点数是有限的，而且通常是2的幂次方，因此无法实现完美的采样，即无法把频率轴分得足够密集，从而会产生离散化误差。因此，为了最小化采样误差，通常会在频率轴上加入一个偏移量0.5，使得采样点的中心落在整数点上，这样可以尽可能减小离散化误差。此外，加上偏移量0.5还有一个好处，就是可以把频率轴上的采样点对应到时域上的采样点，这样可以更直观地理解DFT的计算过程和结果。因此，k=floor((-Nw/2+0.5):(Nw/2+0.5))的作用是定义了一个从-Nw/2到Nw/2的整数序列，其中序列中心对应的频率为0，以便于计算DFT的频率分量。

（2）x=xn(mod(nx,Nx)+1);
这行代码的作用是生成一个周期性的信号，其周期为xn，长度为KNx，其中K是一个常数，nx是一个从0到KNx-1的整数序列。
具体来说，mod(nx,Nx)的作用是把nx中的所有元素对Nx取模，这样得到的结果是一个长度为KNx的整数序列，每Nx个元素是一组，组内元素相同。例如，如果Nx=5，K=3，那么mod(nx,Nx)的结果是[0 1 2 3 4 0 1 2 3 4 0 1 2 3 4]。
因为xn是一个长度为Nx的向量，所以mod(nx,Nx)得到的整数序列可以作为xn的索引，即mod(nx,Nx)+1表示从xn中取出相应的值。因为MATLAB中的向量是从1开始的，所以需要在索引中加上1。
这样，x=xn(mod(nx,Nx)+1)就得到了一个长度为KNx的周期性信号，其周期为xn，它是通过xn不断重复K次得到的。这种构造方式常用于分析周期性信号的性质。
总之，mod的作用是将nx的取值限定在Nx以内，从而实现对xn向量的循环使用。
运行结果：

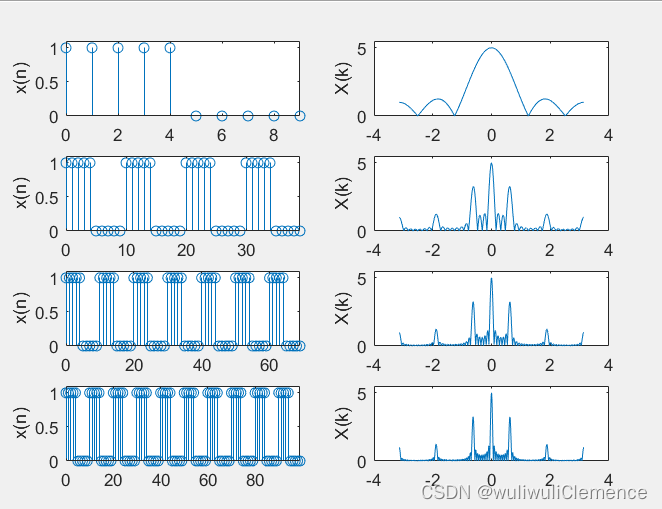
结果分析：
信号序列的周期数越多，频谱越是向几个频点集中，当信号周期数趋近于无穷大时，频谱转化为离散谱。