物理意义:把一个比较复杂的周期运动看成是许多不同频率的简谐振动的叠加。
三角函数系
cos x, sinx, cos2x, sin2x.…, cosnx, sinnx.…
正交性
在[-
π,
π]上正交,即其中任意两个不同的函数之积在[-
π,
π]上的积分等于0.
可以证明:
-
∫−ππcosnxdx=0
-
∫−ππsinnxdx=0
-
∫−ππcosmxcosnxdx=0(m=1,2,3,⋯,n=1,2,3,⋯m̸=n)
-
∫−ππsinmxsinnxdx=0(m=1,2,3,⋯,n=1,2,3,⋯m̸=n)
-
∫−ππsinmxcosnxdx=0(m=1,2,3,⋯,n=1,2,3,⋯)当m=n时
∫−ππ1⋅1dx=2π∫−ππcos2nxdx=π∫−ππsin2nxdx=π(n=1,2,⋯)
设
f(x)是周期为2
π的周期函数,且可逐项积分,利用三角级数得
f(x)=2a0+n=1∑∞(ancosnx+bnsinnx) 想要表达
f(x)得求出
a0,an,bn,对两边进行积分得
∫−ππf(x)dx=∫−ππ2a0dx+n=1∑∞[∫−ππancosnxdx+∫−ππbnsinnxdx]因为
a0,an,bn为常数,利用三角函数的正交性
-
∫−ππcosnxdx=0
-
∫−ππsinnxdx=0
得到
∫−ππf(x)dx=∫−ππ2a0dx=πa0
a0=π1∫−ππf(x)dx
为了求
an,在等式两边
coskx
∫−ππf(x)coskxdx=∫−ππ2a0coskxdx+n=1∑∞I−ππancoskxcosnxdx+∫−ππbncoskxsinnxdx]当k=n时,由三角函数的正交性可知
=∫−ππancoskxcosnxdx=∫−ππancos2nxdxan∫−ππ21+cos2nxdx=anπ其余各项均为零.因此
an=π1∫−ππf(x)cosnxdx(n=1,2,3,⋯)同理
bn=π1∫−ππf(x)sinnxdx(n=1,2,3,⋯)
整理一下得:
⎩⎨⎧an=π1∫−ππf(x)cosnxdxbn=π1∫−ππf(x)sinnxdx(n=0,1,2,⋯)(n=1,2,3,⋯)
an(0开始的),bn称为傅里叶系数。由傅里叶系数组成的三角级数称为傅里叶级数。
例
f(x)={−1,1,−π≤x<00≤x<π
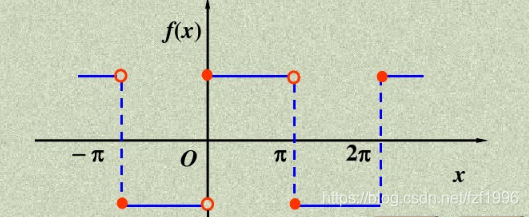
an=π1∫−ππf(x)cosnxdx=π1∫−π0(−1)cosnxdx+π1∫0πcosnxdx=−π1n1sinnx]−π0+π1n1sinnx]0π=0(n=0,1,2,3⋯)
bn=π1∫−ππf(x)sinuxdx=π1∫−π0(−1)sinxdx+π1∫0πsinxdx=π1n1cosnx∣−π0−π1[n1cosnx]0π=nπ2[1−(−1)n]={nπ4,n=1,3,5,⋯0所以
f(x)=n=1∑∞bnsinnx=π4[sinx+31sin3x+⋯+2n−11sin(2n−1)x+⋯]
