目录
Case1: The Queens problem(Max/Min-Conflict)
Case2: Car Sequencing problem(number of violations)
Case3: The Magic Square Problem(degree of violations)
Case5:Traveling Salesman Problem(k-opt)
5.巡回赛问题(traveling tournament problem TTP)
8.1 迭代局部搜索(Iterated Local Search)
Case2: car-sequencing(Transition Abstractions)
Case1: Queens Problem(Transition Abstractions)
1.局部搜索(Local Search)
约束规划从约束出发裁剪搜索空间,一步步给决策变量赋值,而局部搜索直接基于初始解进行局部的调整直到调整后的解满意条件或者最优。对于只需找到解的问题,可以从某个不可行解出发,慢慢调整到可行;对于优化问题,从次优解决方案开始,调整到最优解;对于带约束的优化问题,也有一些针对方法后面会描述。
满意解问题可以转化为优化问题,引入violations这个概念,代表目前的解不满足多少约束,找到解的过程就是最小化violations的过程,以8个皇后为例说明。
Case1: The Queens problem(Max/Min-Conflict)
Max/Min-Conflict:首先选择有最多violations的变量,调整该变量的值从而减小violations。
随机初始解,计算每个queen不满足的约束数量即violations,选择violations最多的变量调整它的位置,如下图,列4的violations为3,调整其位置,计算调整到列4其它位置带来的violations总数变化,将其调整到violations减少最多的格子里,重复上述操作,直到violations=0找到满意解。
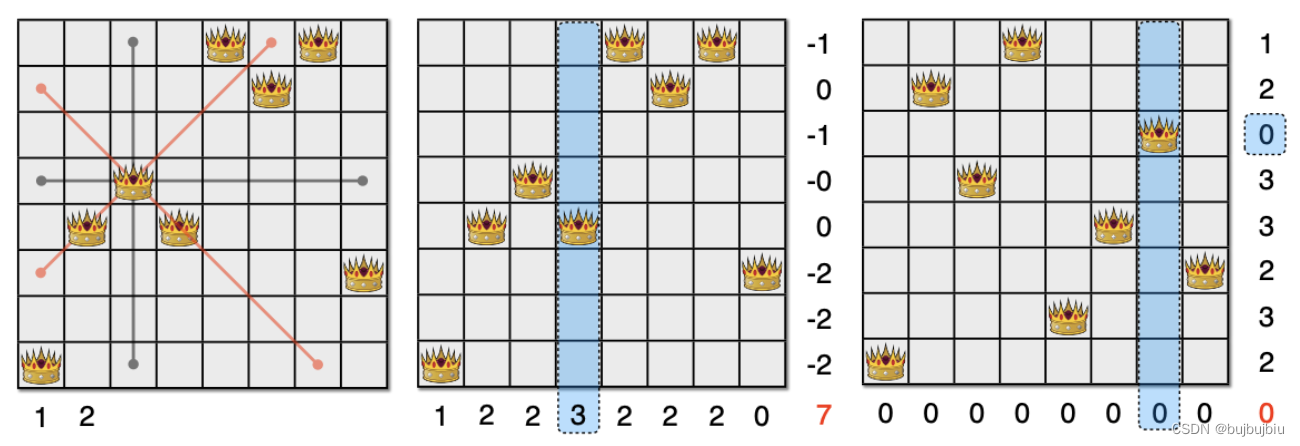
用图表示局部搜索,重复搜索邻域(neighborhood),更新当前找的最优解,再搜索领域。当某个解的领域都没不会比它本身更优时停止搜索,因此局部搜索找到的是局部最优,无法保证全局最优。避免陷入局部最优也是局部搜索中很关键的部分。

2.邻域交换(swap neighborhood)
Case2: Car Sequencing problem(number of violations)
- 对每个option按照容量约束设置滑动窗口,移动窗口计算每行出现不符合约束的次数,标记不合规的option
- 选择violation次数最多的两列交换,如列4和列10
- 更新两个表格,重复上述过程

从这个案例可以看出,在进行局部搜索的过程中,有两类约束:
(1)hard constraints:搜索过程中一直满足,比如每次的解都满足需求约束
(2)soft constraints:搜索过程中可能会违反,比如解满足容量约束
Case3: The Magic Square Problem(degree of violations)
用同样的思路求解Magic Square问题,hard constraint是所有的值都不同,soft constraints是和不等于15,计算每行每列以及斜对角的violation数都是1,然后随机选择交换两个值,交换后可能会出现violation总数还是不变,0/1的violation有时是无用的,大多数移动都会无效,因此可以使用度代替数量。计算所有和与目标值15的差距,选择差距较大的交换值,使其越来越接近目标值
3.旅行商问题(TSP)
Case4:Warehouse Location
仓库集合W, 每个仓库修建费用fw,客户集合C,从每个仓库到客户有运输成本。决策变量有两个:每个仓库是否开放(0/1变量);每个客户分配到哪个仓库。没有约束条件,总成本包括修建成本和运输成本。一旦确定了每个仓库的位置,分配客户就很简单。解的邻域:翻转0/1变量的值。
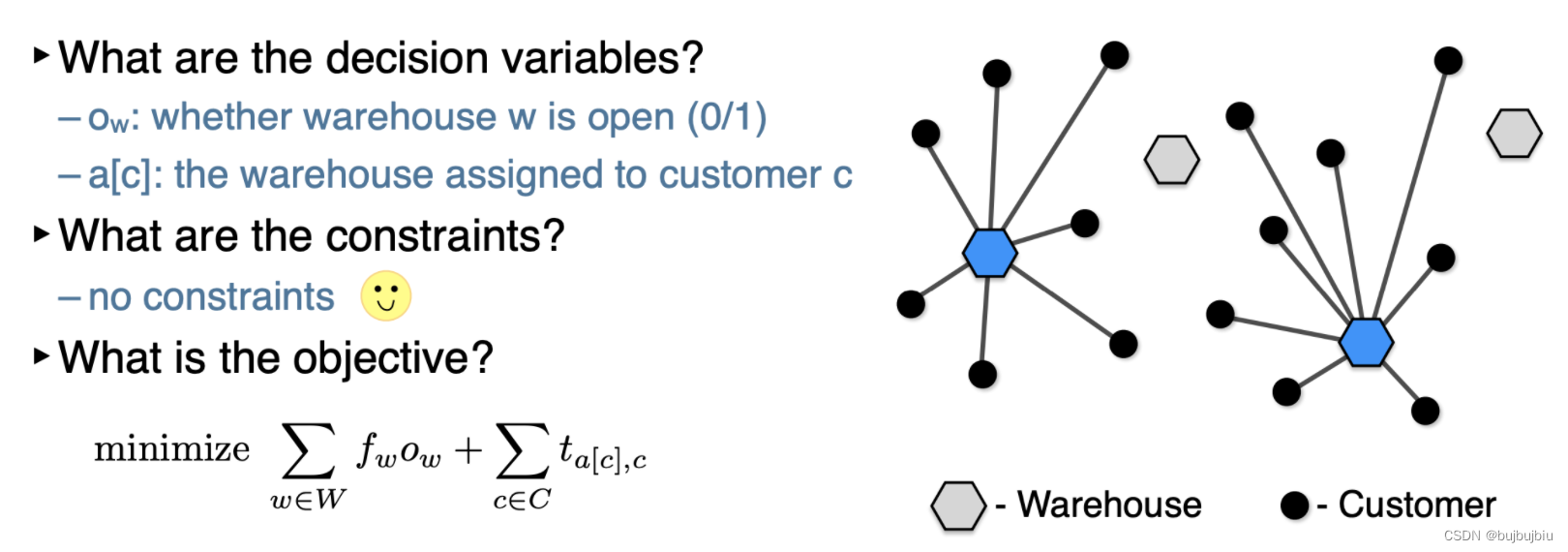
Case5:Traveling Salesman Problem(k-opt)
给定城市及坐标,求最小成本的哈密尔顿回路,即每个点只经过一次且回到原点,k-opt是一种局部搜索方法
(1)2-opt:选择两条不相邻边 ,交换这两条边,判断是否减少了cost
(2)3-opt: 同样交换3条边,解质量比2-opt高但是更耗时
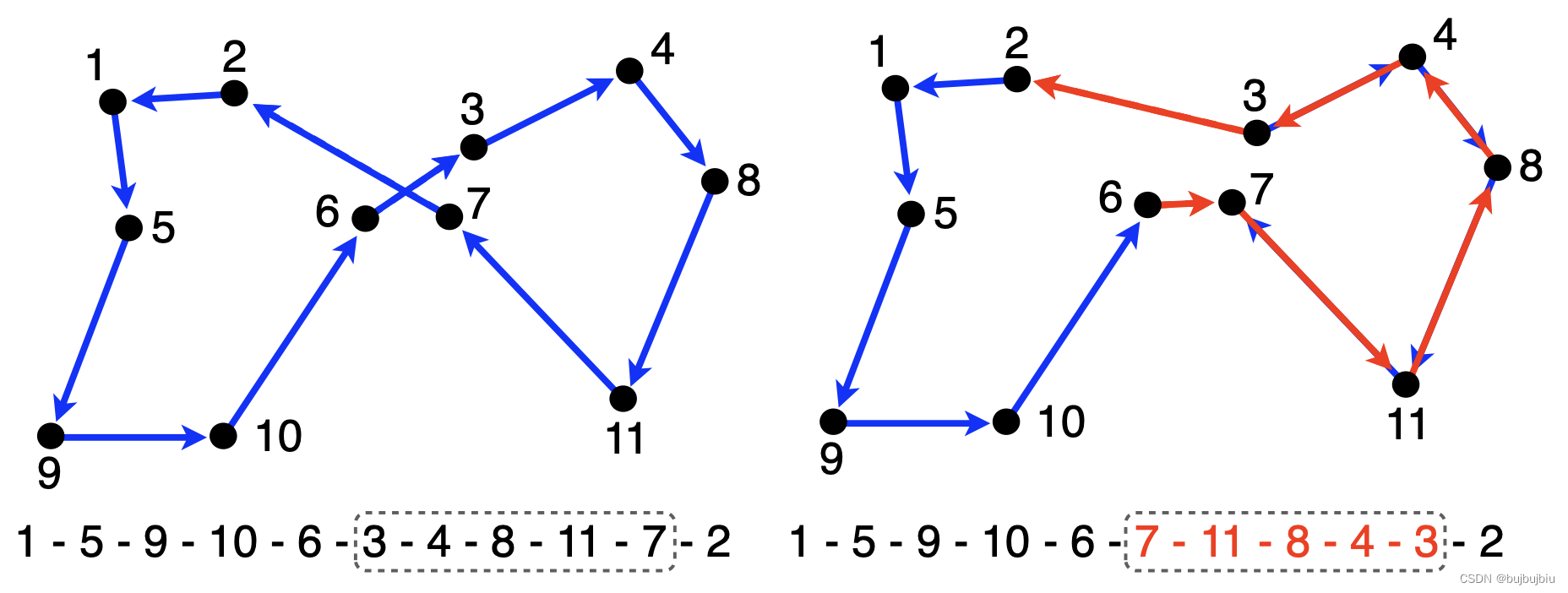
(3)k-opt:同样思路,但是不要关注于怎么交换,而是搜索交换找到更好的序列,每次改进一点,k是一个参数,需要调整确定最佳的k值,随机选择一个点开始,以下图为例
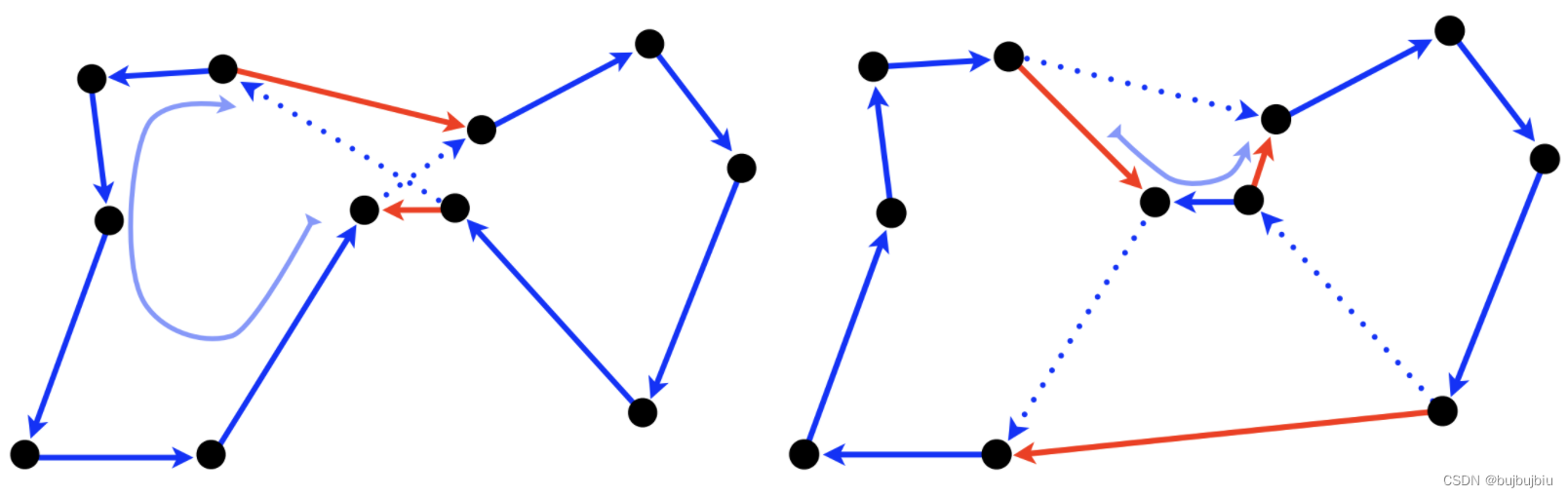
- 从点1开始,连接边为(1,2),选择长度小于(1,2)的边(2,3)并连接,去掉原本与点3相连的边(4,3),连接边(1,4),但是不是真的连接,计算新的cost
- 重复上述过程,下图为每一次更新序列的图,红实线为增加的边,红虚线表示继续从这条边开始找到交换的序列。最后一步,从边(1,8)开始,找不到边(8,~)更短,因此停止,开始换一个顶点更新

- 从新的顶点出发,重复上面过程,如下图已找到最优解

4.图着色问题(graph coloring GCP)
使用局部搜索解决图着色问题时需要考虑两个问题:
- optimization(最优性):减少颜色数
- feasibility(可行性):满足相邻不同色的约束
将两个问题融合到LC中有以下三种思路
(1)sequence of feasibility problems(可行解序列)
找到有k个颜色的初始解,消除颜色k,随机将颜色为k的顶点用颜色为[1,k-1]代替,通过减少violation找到k-1个颜色的解
(2)staying in the feasible space
设C(i)为颜色为i的顶点集合,优化目标为最小化颜色数量,可以转化为最大化顶点集合长度,即让更多的点颜色相同,在同一个集合里。 领域为改变某个顶点的颜色,但是为了保证解可行,改变某个顶点的颜色就需要改变其它顶点的颜色,此处提出Richer neighborhoods的概念,即领域是从问题结构出发,一次会改变多个部分,使用Kemp Chains修改颜色向neighborhoods移动
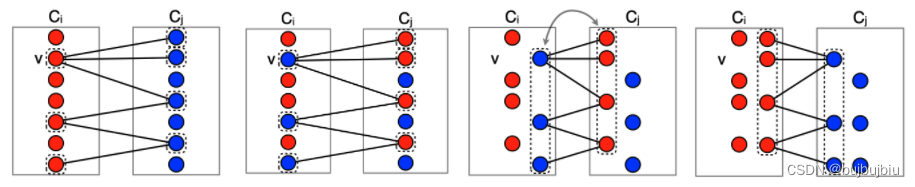
(3)Explore both feasible and infeasible colorings
搜索过程时要同时保证减少颜色数量且解可行,修改目标函数平衡feasibility和optimality,定义两个顶点颜色相同的边为bad edge,B(i)为C(i)里bad edge集合,目标函数如下,最小化|B(i)|,最大化|C(i)|,函数这样设计能保证:该目标的局部最优一定是可行解。
推导过程如下:假设现在解为C(1)....C(k),从某个不为空的B(i)>=1中选择一条边,边的其中一个顶点颜色改为k+1,那么通过计算可知目标函数至少减少了2,说明对于一个非可行的解,总能找到方法让目标函数减少2,说明这不是局部最优。非可行解一定不是局部最优,局部最优一定是可行解。

5.巡回赛问题(traveling tournament problem TTP)
n个队,每个队和其它队各打两次,每队每周打一次,a@b表示a去b的场地打,有两个约束:
- atmost constraint:不能超过连续三次都在home或者都在其它地方打
- no repeat constraint:a@b不能出现在b@a后面,即不能连着两周两个队伍一样
如下右图:假设有6只队伍,则总共有10周,例如队1,在第一周和6打,第二周去到2的场地和2打,两个约束体现在调度表里为:每行@或者无@单元格出现不能连续超过三次,每行相邻两个格子数字不一样。还有一个冗余约束,某列出现ab则也要满足b@a,优化目标是最小化总行程。

总共有5中方式向Neighborhood移动:
- Swap Homes: a@b变成ab,ab变成a@b

- Swap Rounds:交换某两周的安排

- Swap Teams: 选择两个队伍交换彼此的安排,不包括两队本身的比赛,交换后调整可行解


- Swap Partial Rounds:交换某队某两周的安排然后调整到可行解

- Swap Partial Teams:交换某周某两个队伍的比赛对象然后调整到可行解

6.连通性(Connectivity)
对于局部搜索,其最终效果还取决于搜索空间(解空间)的特征,如下图所示,用深色表示最优解。当解空间如左,可以通过局部搜索向最优解转移;当解空间如中,容易陷入局部最优,可以通过某些方法跳出局部最优;当解空间如右,空间是不连通的,任何局部搜索都无法找到最优解。因此在使用LC解决问题时,首先要判断解空间是否连通。

前面遇到的Graph Coloring,Car Sequencing,Traveling Salesman Problem都满足连通性,以TSP的2-opt为例说明,每次交换后实际上是在翻转两个顶点之间的序列,通过翻转每个位置都有可能出现所有顶点,即从某一初始解出发能到达任何解。
7. 启发式方法(heuristics)
首先回顾一下基础的局部搜索过程,从某个解(state)出发,找到它的邻域N(s),从N(s)中筛选出合法的可行的邻域L(N(s),s),从可行邻域中选择某个解S(L(N(s),s),s)作为移动目标。

如何选择下一个neighbor是非常重要的部分,包括以下两大类
- 启发式方法(Heuristics):根据当前状态及邻域信息,决定下一个neighbor,使搜索朝着局部最优的方向,比如2-opt
- 元启发式方法(Metaheuristics):在启发式方法基础上做到避免陷入局部最优,使搜索朝着全局最优的方向,比如GA,SA
本节只介绍启发式方法,某个解的neighbor可能能局部改进,也可能保持原样,也可能有潜在的退化,从L(N(s),s)到S(L(N(s),s),s)有以下思路
- Best neighbor:探索所有的可行邻域后选择最好的解

- First neighbor:选择第一个可行的解,避免探索所有的可行邻域

- Multi-Stage Heuristics:分多步实现,比如在8个皇后问题中,先选择变量再分配值,在第一步选择使用greedy选择violations最多的变量,也可以随机选择一个变量
- Random Walks:随机选择

8.元启发式算法(Metaheuristics)
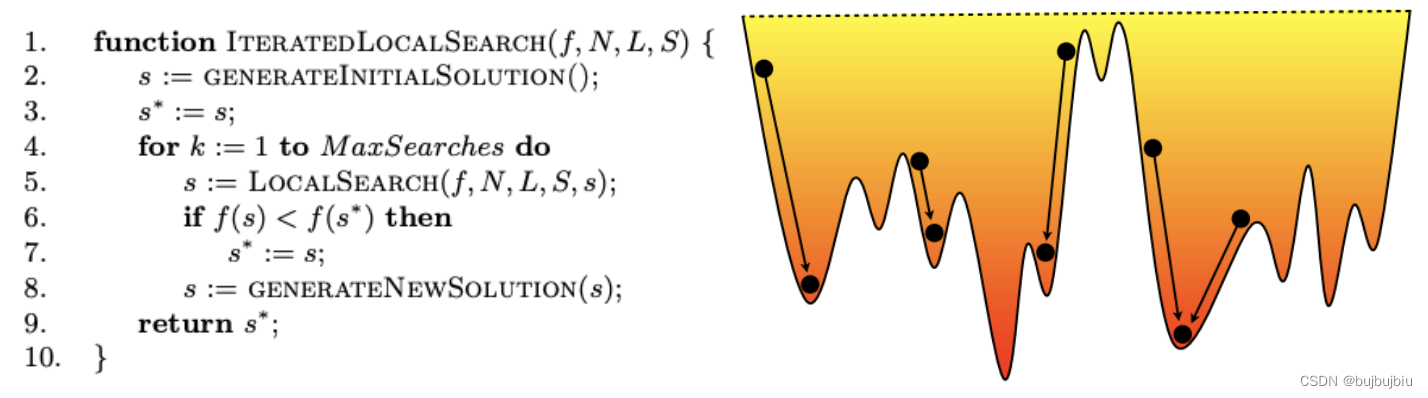
8.1 迭代局部搜索(Iterated Local Search)
多次从不同的起点开始迭代搜索,如下图,每次执行S(L(N(s),s),s)后更新最优值,然后重新生成初始解。可以将迭代局部搜索和其它元启发式算法结合,实现多次重启搜索。
8.2 模拟退火(Simulated Annealing)
模拟退火SA来源于Metropolis Heuristic方法,选择一个邻域解,如果该解的目标值优于原先解的目标值,可直接移动到该解,否则按照一定的概率选择该解。概率为原目标值和新目标值差和t的比值的指数,其中t为超参数需要调整。
在Metropolis Heuristic方法中,如果t比较大,接收退化解的概率也会变大,如果t比较小,接收退化解的概率会变小,但是也容易陷入局部最优。因此参考水晶制作过程,为了减少缺陷,制作温度会慢慢下降。因此在Metropolis Heuristic中可以动态调整t的值,也就是模拟退火算法的思路,最开始搜索时t比较大,更倾向于探索新解,逐步降低t的值,最后进行局部的改进

Simulated Annealing能保证收敛到全局最优,但是有些场景下比暴力全局搜索还慢,实际应用中,SA表现较好的测试集有TTP,scheduling等。为了加快搜索速度,可以适当调整t的下降速度。在SA中可以使用的一些小技巧:重设初始解,重设温度等
8.3 禁忌搜索(Tabu Search)
用tabu list保存已经探索过的解tabu node,每次选择不在tabu list里的邻域可行解,更多内容见下一节。除了上述三种元启发式方法,还有变邻域搜索(variable neighborhood search),引导式局部搜索(guided local search),蚁群算法(ant-colony optimization),混合进化算法(hybrid evolutionary algorithms),散点搜索(scatter search)等。

9.禁忌搜索扩展
(1)Short-Term Memory+Transition Abstractions
前文已经描述过禁忌搜索的核心思想是:不逃探索已经探索过的节点。因此需要一个tabu list存储所有已经探索过的node。这样的思路有一个问题:维护所有的tabu node在tabu list是非常耗时且占用内存的,因此提出Short-Term Memory的方法,有两个方面的改进
- tabu list大小:只保留一部分已经探索过的node;可以动态的调整列表的大小
- tabu node存储结构:保存状态的转移抽象而非状态本身
通过car-sequencing案例说明该过程
Case2: car-sequencing(Transition Abstractions)
假设每次move只是交换某两个slot,用(a(i),b(i))表示在第i步交换了a(i)和b(i),如果某个领域解可以通过交换(a(i),b(i))获取,那么该解被禁止。如何实现?假设当前迭代计数为it,tabu list长度为L,用数据结构tabu[i,j]表示下一次迭代i和j会被交换,如果tabu[i,j] > it,那么这种交换是允许的,tabu[i,j]更新为it+L。即禁忌的不再是整个解(组合),而是某个交换操作。即便某步所有的mo ve都被禁止了,随着迭代步长的增加,总会出现不被禁止的交换操作。这种改变不会使每次交换的解质量更好,但是能极大的提高计算效率。如下左图,首先找到NotTabu然后更新tabu[i,j]以及tabu[j,i],根据目标函数值决定是否更新当前最优解。

使用这种转移抽象以及限制长度作为禁忌选择效果可强可弱:
- Too weak:只考虑固定长度的tabu list可能会重复探索之前探索过的node
- Too strong:可能会阻止搜索未探索过的node,因此禁忌的是交换操作,要比禁忌某个完整的解效果更强
为了加强这种转移抽象,可以存储每次转移以及目标函数值,(ai,bi,fi,fi+1)表示在step i交换ai和bi,目标函数值从fi变成fi+1,因此如果可以交换(ai,bi)或者某个邻域可行解,且f(s)= fi和f(n)=fi+1,那么该解被禁止。
Case1: Queens Problem(Transition Abstractions)
同样思路,在Queens Problem里在tabu list中存储(x,v),表示某列不能赋值v,比直接存储所有的解要更快

(2)Aspiration
如果某个move被禁止,但是结果变好了,也可以使用,同时考虑tabu list和目标函数值

(3)Long-Term Memory
- Intensification:存储高质量的解,阶段性的返回到这些解
- Diversification:如果当前搜索找不到改进,改变当前状态,比如随机改变某些变量的值
- Strategic oscillation:调整在可行解和不可行解搜索时间比例
这些技巧也可以在SA中使用
10.TSP编程作业
对求解时间,解质量要求比较高,分别使用2-opt,k-opt,SA求解,代码见本人github
关于TSP相关算法实现细节可见Implementing Lin-Kernighan in Python